Random / noise functions for GLSL

Question

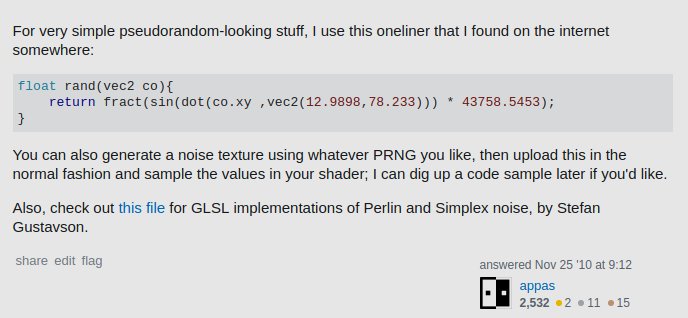
As the GPU driver vendors don't usually bother to implement noiseX in GLSL, I'm looking for a "graphics randomization swiss army knife" utility function set, preferably optimised to use within GPU shaders. I prefer GLSL, but code any language will do for me, I'm ok with translating it on my own to GLSL.

Specifically, I'd expect:

a) Pseudo-random functions - N-dimensional, uniform distribution over [-1,1] or over [0,1], calculated from M-dimensional seed (ideally being any value, but I'm OK with having the seed restrained to, say, 0..1 for uniform result distribution). Something like:

float random  (T seed);
vec2  random2 (T seed);
vec3  random3 (T seed);
vec4  random4 (T seed);
// T being either float, vec2, vec3, vec4 - ideally.

b) Continous noise like Perlin Noise - again, N-dimensional, +- uniform distribution, with constrained set of values and, well, looking good (some options to configure the appearance like Perlin levels could be useful too). I'd expect signatures like:

float noise  (T coord, TT seed);
vec2  noise2 (T coord, TT seed);
// ...

I'm not very much into random number generation theory, so I'd most eagerly go for a pre-made solution, but I'd also appreciate answers like "here's a very good, efficient 1D rand(), and let me explain you how to make a good N-dimensional rand() on top of it..." .

Clypeate

There is a bunch of great Pseudo-random functions over here: shadertoy.com/view/4djSRW – Aback

A good paper, with performance and quality test results for different hash functions, is at jcgt.org/published/0009/03/02). Also shadertoy.com/view/XlGcRh – Erickaericksen

If you're looking for just a time-based random (eg not a different random per-pixel), may want to consider using a uniform – Ephemeral

Answer 1

For very simple pseudorandom-looking stuff, I use this oneliner that I found on the internet somewhere:

float rand(vec2 co){
    return fract(sin(dot(co, vec2(12.9898, 78.233))) * 43758.5453);
}

You can also generate a noise texture using whatever PRNG you like, then upload this in the normal fashion and sample the values in your shader; I can dig up a code sample later if you'd like.

Also, check out this file for GLSL implementations of Perlin and Simplex noise, by Stefan Gustavson.

Kenya

How do you use vec2 co? is it the range? seed? – Braided

It is the seed. Eg: assembla.com/code/ffgl/subversion/nodes/trunk/Source/… – Kenya

Note that anything using trigonometric functions in GLSL has undefined precision. I have run into problems with a random number generator, dependent on sin(), not generating the same results on ATI and NVIDIA. The accepted answer here may show the same problem, but I have not confirmed it. Gustavson's solution does not appear to use any function with undefined precision; thus it should probably be fine to use while expecting roughly the same result on different platforms. – Unsphere

Beware of low-precision floating-point fragment shaders with this algorithm (e.g., S3's ARM Mali): #11294128. The github.com/ashima/webgl-noise project does not seem to have lowp issues. – Cycloid

FWIW, the function described here is discussed in more detail here. – Superordinate

FYI: The distribution of that function is horrible. – Terbecki

I'm newb in GLSL, can anybody explain why co.xy is used, instead of co? – Satchel

@Satchel Probably a left over from a vec3 variant. I've seen this hideous "hash" function in dozens of shaders at Shadertoy. – Moneymaking

if it weren't for the awesome 6 character edit rule, I would edit the space before the comma so it only appears after... I'm sure 100s of developers have copy pasted this and then manually corrected it in their code... -.- – Clerc

Does the input to this function need to be between [0, 1) ? – Fina

@Fina no, as the return value gets processed by fract and the input is simply fed into a sine function. – Kenya

sin() is likely to be slow, and as other people have pointed out, this results in a sloppy distribution and might work differently on different hardware. I don't know why this answer is popular. Spatial's answer is much better. – Antlion

This comes from thebookofshaders.com/10. Read their article for a detailed explanation. co are normalized screen coordinates – Colobus

I had definitive lines at large scales in 3-D. Going off one of the suggestions by @hoangdado, I modded the contents of sin by PI (sin(mod(..., PI))) which fixed it completely. – Longshore

Running sample – Ephemeral

Answer 2

It occurs to me that you could use a simple integer hash function and insert the result into a float's mantissa. IIRC the GLSL spec guarantees 32-bit unsigned integers and IEEE binary32 float representation so it should be perfectly portable.

I gave this a try just now. The results are very good: it looks exactly like static with every input I tried, no visible patterns at all. In contrast the popular sin/fract snippet has fairly pronounced diagonal lines on my GPU given the same inputs.

One disadvantage is that it requires GLSL v3.30. And although it seems fast enough, I haven't empirically quantified its performance. AMD's Shader Analyzer claims 13.33 pixels per clock for the vec2 version on a HD5870. Contrast with 16 pixels per clock for the sin/fract snippet. So it is certainly a little slower.

Here's my implementation. I left it in various permutations of the idea to make it easier to derive your own functions from.

/*
    static.frag
    by Spatial
    05 July 2013
*/

#version 330 core

uniform float time;
out vec4 fragment;



// A single iteration of Bob Jenkins' One-At-A-Time hashing algorithm.
uint hash( uint x ) {
    x += ( x << 10u );
    x ^= ( x >>  6u );
    x += ( x <<  3u );
    x ^= ( x >> 11u );
    x += ( x << 15u );
    return x;
}



// Compound versions of the hashing algorithm I whipped together.
uint hash( uvec2 v ) { return hash( v.x ^ hash(v.y)                         ); }
uint hash( uvec3 v ) { return hash( v.x ^ hash(v.y) ^ hash(v.z)             ); }
uint hash( uvec4 v ) { return hash( v.x ^ hash(v.y) ^ hash(v.z) ^ hash(v.w) ); }



// Construct a float with half-open range [0:1] using low 23 bits.
// All zeroes yields 0.0, all ones yields the next smallest representable value below 1.0.
float floatConstruct( uint m ) {
    const uint ieeeMantissa = 0x007FFFFFu; // binary32 mantissa bitmask
    const uint ieeeOne      = 0x3F800000u; // 1.0 in IEEE binary32

    m &= ieeeMantissa;                     // Keep only mantissa bits (fractional part)
    m |= ieeeOne;                          // Add fractional part to 1.0

    float  f = uintBitsToFloat( m );       // Range [1:2]
    return f - 1.0;                        // Range [0:1]
}



// Pseudo-random value in half-open range [0:1].
float random( float x ) { return floatConstruct(hash(floatBitsToUint(x))); }
float random( vec2  v ) { return floatConstruct(hash(floatBitsToUint(v))); }
float random( vec3  v ) { return floatConstruct(hash(floatBitsToUint(v))); }
float random( vec4  v ) { return floatConstruct(hash(floatBitsToUint(v))); }





void main()
{
    vec3  inputs = vec3( gl_FragCoord.xy, time ); // Spatial and temporal inputs
    float rand   = random( inputs );              // Random per-pixel value
    vec3  luma   = vec3( rand );                  // Expand to RGB

    fragment = vec4( luma, 1.0 );
}

---

Screenshot:

I inspected the screenshot in an image editing program. There are 256 colours and the average value is 127, meaning the distribution is uniform and covers the expected range.

Roeder

+1 for a good idea and implementation. I would question the claim that because there are 256 colors and the average value is 127, the distribution must be uniform (in the strict sense). It might be uniform, but I don't think we know that yet. E.g. a bell curve distribution could have the same average and number of colors, but wouldn't be uniform. – Erickaericksen

Well, it's good enough for most applications that don't need uniformity. :-) – Veron

It seems to be very uniform, by my perception of the histogram.... I'd say it's good enough for most applications that need uniformity as well. (The only values that seem to be generated less than the others are 0 and 255) – Crayton

Thanks. My probability is rusty. Having looked at the GCN instruction set, this should be very fast on newer hardware because they directly support bitfield operations in their instruction sets. The tests I did ran on older hardware. – Roeder

Very nice, much less artefacts than the fract(sin(dot(...))) method. To port to HLSL use asFloat and asUint functions instead of the floatBitsToXXX functions. – Pearson

How can I implement a vec3 random(vec3 v) overload of this method? – Dicho

@PedroHenrique: What about vec3(random(v.x), random(v.y), random(v.z))? – Readymix

Answer 3

Gustavson's implementation uses a 1D texture

No it doesn't, not since 2005. It's just that people insist on downloading the old version. The version that is on the link you supplied uses only 8-bit 2D textures.

The new version by Ian McEwan of Ashima and myself does not use a texture, but runs at around half the speed on typical desktop platforms with lots of texture bandwidth. On mobile platforms, the textureless version might be faster because texturing is often a significant bottleneck.

Our actively maintained source repository is:

https://github.com/ashima/webgl-noise

A collection of both the textureless and texture-using versions of noise is here (using only 2D textures):

http://www.itn.liu.se/~stegu/simplexnoise/GLSL-noise-vs-noise.zip

If you have any specific questions, feel free to e-mail me directly (my email address can be found in the classicnoise*.glsl sources.)

Circuit

Yes, the implementation I'm referring to, your code on davidcornette.com that @dep linked to, does use a 1D texture: glBindTexture(GL_TEXTURE_1D, *texID); etc. It's not clear what you mean by "the link you supplied", since you quote from my answer but that answer didn't link to your implementation. I will update my answer to clarify what I'm referring to and reflect the new information you've given. Characterizing people as "insisting" on downloading the old version is a distortion that does not do you credit. – Erickaericksen

P.S. You may want to write to David Cornette (he has contact info at davidcornette.com) and ask him to change his link on davidcornette.com/glsl/links.html to link to your source repo. I'll email him too. – Erickaericksen

P.P.S. Can you clarify, which version uses only 8-bit 2D textures? Sounds like it might be a good option for certain platforms... – Erickaericksen

Answer 4

Gold Noise

// Gold Noise ©2015 [email protected]
// - based on the Golden Ratio
// - uniform normalized distribution
// - fastest static noise generator function (also runs at low precision)
// - use with indicated fractional seeding method. 

float PHI = 1.61803398874989484820459;  // Φ = Golden Ratio   

float gold_noise(in vec2 xy, in float seed){
       return fract(tan(distance(xy*PHI, xy)*seed)*xy.x);
}

See Gold Noise in your browser right now!

This function has improved random distribution over the current function in @appas' answer as of Sept 9, 2017:

The @appas function is also incomplete, given there is no seed supplied (uv is not a seed - same for every frame), and does not work with low precision chipsets. Gold Noise runs at low precision by default (much faster).

Southwestwardly

Thanks for posting this. Would you consider posting a runnable version, e.g. at shadertoy.com, so people can try it out in-browser? – Erickaericksen

Here is an example of Gold Noise in the wild, a dithering application: shadertoy.com/view/XdGczW – Southwestwardly

I dont think this is any different than other noise functions. what is your prove that this has special properties. just because you use bunch of irrational numbers doesn't make it special. – Kierakieran

It has superior distribution to similar functions, and is faster because can also run at low precision, as clearly stated in the comments. These are the only properties that matter in a fragment shader noise function – Southwestwardly

@Dominic: "It has superior distribution to similar functions": this has to be proven. tan() is really ill-conditioned. both tan() near pi/2 and sqrt() near zero are very likely to produce different results on different hardwares since all fract(non-linear*big) are based on less significant bits. Small or high input values will impact it too. Also, bits dynamics probably varies a lot too depending on locations. – Arleta

NB: Nowadays GLSL have integers, so there is no longer any reason not to use "serious" int-based hash generators when quality distribution (and dynamics) is required, with similar performances. ( excepted for very low-end devices ). – Arleta

Similar functions (eg. appas' above) do not run at low precision and exhibit diagonal banding, the most obvious artifact of inferior distribution, so the proof is already given. Also the latest 'hardwares' (sic) have embedded noise generators, so your argument for them is moot. Please understand that SOC (ie mobile) GLES is the single most prevalent shader platform, is often low precision and has no embedded noise functions. This is toward the point of Gold Noise that you have perhaps not grasped. – Southwestwardly

@user151496 Not broken. Please do not be rude in these comments. The docs clearly state "use with indicated fractional seeding method". Write your own noise function if you want arbitrary seeding methods. – Southwestwardly

What's the point of doing distance(xy*PHI, xy)? Isn't it always just length(xy) * (PHI-1) ? – Navarra

gold_noise really seems to give better results than frac(sin(...)) but all this fuss about irrational numbers is silly. To the GPU, all numbers are finite, so there isn't any benefit of using an actual irrational number. I used PHI = 1234.345 and seed = 0.5 and the randomness looked just as good, if not even slightly better. Either way, gold_noise isn't perfect either; so instead have a look at actual (= integer) hash functions, e.g. xxhash or pcg. – Flavouring

@Flavouring Your silly, hacky and shockingly erroneous "PHI = 1234.345" (sic) causes obvious banding artifacts when used in Gold Noise, as anyone can confirm. The inferior random distribution is obviously far worse than using actual PHI. Did you not even test it? Also Gold Noise is a portable noise function that can be used anywhere esp. when native hashing and noise functions are not available on a given platform. – Southwestwardly

On my Pixel 6 device, it has worse performance than the well-known fract(sin()). Your distance() call implies a sqrt() which explains it. – Sporophore

@I33t please read the answer and the documentation. If you are going to benchmark something, provide details. Don't just throw out an unsupported opinion. That is just rude anonymous trolling. – Southwestwardly

Answer 5

After the initial posting of this question in 2010, a lot has changed in the realm of good random functions and hardware support for them.

Looking at the accepted answer from today's perspective, this algorithm is very bad in uniformity of the random numbers drawn from it. And the uniformity suffers a lot depending on the magnitude of the input values and visible artifacts/patterns will become apparent when sampling from it for e.g. ray/path tracing applications.

There have been many different functions (most of them integer hashing) devised for this task, for different input and output dimensionality, most of which are being evaluated in the 2020 JCGT paper Hash Functions for GPU Rendering. Depending on your needs you could select a function from the list of proposed functions in that paper and simply from the accompanying Shadertoy. One that isn't covered in this paper but that has served me very well without any noticeably patterns on any input magnitude values is also one that I want to highlight.

Other classes of algorithms use low-discrepancy sequences to draw pseudo-random numbers from, such as the Sobol squence with Owen-Nayar scrambling. Eric Heitz has done some amazing research in this area, as well with his A Low-Discrepancy Sampler that Distributes Monte Carlo Errors as a Blue Noise in Screen Space paper. Another example of this is the (so far latest) JCGT paper Practical Hash-based Owen Scrambling, which applies Owen scrambling to a different hash function (namely Laine-Karras).

Another possibility are so called "Congruential Generators", either "Linear Congruential Generators" (LCG) or "Permuted Congruential Generators" (PCG), which differ from the hash-based algorithms in that LCGs and PCGs have a "state" and an associated function mutating this state from which the pseudo-random numbers are drawn. So, they do not rely on any "input" for computing a hash, but merely shift/permute/mutate a state which then carries across multiple invocations of the function. One application of PCGs can be found in Nvidia's "Mini Path-Tracer Tutorial".

Yet other classes use algorithms that produce noise patterns with desirable frequency spectrums, such as blue noise, that is particularly "pleasing" to the eyes.

(I realize that good StackOverflow answers should provide the algorithms as source code and not as links because those can break, but there are way too many different algorithms nowadays and I intend for this answer to be a summary of known-good algorithms today)

Litotes

Answer 6

There is also a nice implementation described here by McEwan and @StefanGustavson that looks like Perlin noise, but "does not require any setup, i.e. not textures nor uniform arrays. Just add it to your shader source code and call it wherever you want".

That's very handy, especially given that Gustavson's earlier implementation, which @dep linked to, uses a 1D texture, which is not supported in GLSL ES (the shader language of WebGL).

Erickaericksen

This is the best answer to OP's b) noise type request! Here is a direct link github.com/ashima/webgl-noise. There are 2d, 3d and 4d versions ready as GLSL 120 code. – Intercolumniation

Answer 7

Do use this:

highp float rand(vec2 co)
{
    highp float a = 12.9898;
    highp float b = 78.233;
    highp float c = 43758.5453;
    highp float dt= dot(co.xy ,vec2(a,b));
    highp float sn= mod(dt,3.14);
    return fract(sin(sn) * c);
}

Don't use this:

float rand(vec2 co){
    return fract(sin(dot(co.xy ,vec2(12.9898,78.233))) * 43758.5453);
}

You can find the explanation in Improvements to the canonical one-liner GLSL rand() for OpenGL ES 2.0

Klopstock

I skimmed over the article but I am still not sure, is 3.14 in mod an approximation of pi ? – Plantagenet

I don't swallow this. I would rephrase it as "on an hypothetically crappy system that doesn't guarantee any precision to float operators and would be stupid enough to not already wrap the sin argument (does this really exist ?), it can improve to mod the content of sine. " Also I'm a bit nervous about bias when using a huge approx of pi, but large c value might save the day. – Arleta

@FabriceNEYRET On both my notebooks (one with Intel UHD Graphics 620, the other reports an Nvidia Quadro T1000), Muddy Cavern starts showing grid patterns on the walls after 32 seconds. With mod(n, 6.2831853), no such problem. That suggests mod does make a difference, at least on some GPUs. The author of the article admits that employing both mod and highp might be overkill. I suppose some research would be required to get to the bottom of this. – Tourism

@Ruud Helderman: yep, meanwhile on Shadertoy some had confirmed this for low-end GPUs. For the Nvidia it's more surprising ( + they are generaly even implementing maths and IEEE beyond the GLSL specs). Oh my... – Arleta

@FabriceNEYRET Don't panic, it could still be a weird coincidence; like a combination of (1) reduced precision as the seed grows, (2) the seed making leaps that happen to approximate multiples of 2π, (3) the 2π modulus I introduced being slightly inaccurate, breaking the regularity, giving the false impression of an improvement. – Tourism

well i have tried most of the examples posted here where i had a strange line distortion using a perlin based on the first.... i tried this one you posted and it makes a smooth noise :) ... sometimes just try them lol – Araucanian

Answer 8

hash: Nowadays webGL2.0 is there so integers are available in (w)GLSL. -> for quality portable hash (at similar cost than ugly float hashes) we can now use "serious" hashing techniques. IQ implemented some in https://www.shadertoy.com/view/XlXcW4 (and more)

E.g.:

  const uint k = 1103515245U;  // GLIB C
//const uint k = 134775813U;   // Delphi and Turbo Pascal
//const uint k = 20170906U;    // Today's date (use three days ago's dateif you want a prime)
//const uint k = 1664525U;     // Numerical Recipes

vec3 hash( uvec3 x )
{
    x = ((x>>8U)^x.yzx)*k;
    x = ((x>>8U)^x.yzx)*k;
    x = ((x>>8U)^x.yzx)*k;

    return vec3(x)*(1.0/float(0xffffffffU));
}

Arleta

Answer 9

Just found this version of 3d noise for GPU, alledgedly it is the fastest one available:

#ifndef __noise_hlsl_
#define __noise_hlsl_

// hash based 3d value noise
// function taken from https://www.shadertoy.com/view/XslGRr
// Created by inigo quilez - iq/2013
// License Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.

// ported from GLSL to HLSL

float hash( float n )
{
    return frac(sin(n)*43758.5453);
}

float noise( float3 x )
{
    // The noise function returns a value in the range -1.0f -> 1.0f

    float3 p = floor(x);
    float3 f = frac(x);

    f       = f*f*(3.0-2.0*f);
    float n = p.x + p.y*57.0 + 113.0*p.z;

    return lerp(lerp(lerp( hash(n+0.0), hash(n+1.0),f.x),
                   lerp( hash(n+57.0), hash(n+58.0),f.x),f.y),
               lerp(lerp( hash(n+113.0), hash(n+114.0),f.x),
                   lerp( hash(n+170.0), hash(n+171.0),f.x),f.y),f.z);
}

#endif

Carpio

Gold Noise (above) is then obviously fastest, since it has far fewer operations and only performs one hash - this one calls its hash fuction 8 times, while performing nested linear interpolations (lerps). Also this one has inferior distribution especially at low precision. – Southwestwardly

Oh good point, it's a perlin noise type graph from shadertoh by Inigo Quilez. Nice code Dominic ill check it l8r – Carpio

@Fabrice You don't seem to understand the OP's question, my answer, my code or my comment.. Gold Noise is continuous by the OPs definition - it accepts uv and a seed and proves it by providing a shader. Everything about your comment is wrong. You keep confusing hash functions with pseudo random noise functions. They are not the same. Noise functions have no requirement to generate unique identifiers like hash functions (the actual whole point of hashing). – Southwestwardly

Please please please, Dominic, read more and learn more before claiming things about terms you think you understand while it's not the case. Not only these terms are totally precise and well define in litterature, plus I do work in the field, but also the OP proves he understood the terms by the examples he gave after. Hint: "continuous" + "noise" + "like Perlin". en.wikipedia.org/wiki/Perlin_noise – Arleta

Continuous is onle a case of adding a loop clause, many noise functions loop and degrade after a certain way because of bit rounding especially for graphics. Guys its just a communication breaksown from you, use your time for important research. – Carpio

Please Fabrice, write your own noise shader if you want to critique Gold Noise. – Southwestwardly

Answer 10

A straight, jagged version of 1d Perlin, essentially a random lfo zigzag.

half  rn(float xx){         
    half x0=floor(xx);
    half x1=x0+1;
    half v0 = frac(sin (x0*.014686)*31718.927+x0);
    half v1 = frac(sin (x1*.014686)*31718.927+x1);          

    return (v0*(1-frac(xx))+v1*(frac(xx)))*2-1*sin(xx);
}

I also have found 1-2-3-4d perlin noise on shadertoy owner inigo quilez perlin tutorial website, and voronoi and so forth, he has full fast implementations and codes for them.

Carpio

Answer 11

I have translated one of Ken Perlin's Java implementations into GLSL and used it in a couple projects on ShaderToy.

Below is the GLSL interpretation I did:

int b(int N, int B) { return N>>B & 1; }
int T[] = int[](0x15,0x38,0x32,0x2c,0x0d,0x13,0x07,0x2a);
int A[] = int[](0,0,0);

int b(int i, int j, int k, int B) { return T[b(i,B)<<2 | b(j,B)<<1 | b(k,B)]; }

int shuffle(int i, int j, int k) {
    return b(i,j,k,0) + b(j,k,i,1) + b(k,i,j,2) + b(i,j,k,3) +
        b(j,k,i,4) + b(k,i,j,5) + b(i,j,k,6) + b(j,k,i,7) ;
}

float K(int a, vec3 uvw, vec3 ijk)
{
    float s = float(A[0]+A[1]+A[2])/6.0;
    float x = uvw.x - float(A[0]) + s,
        y = uvw.y - float(A[1]) + s,
        z = uvw.z - float(A[2]) + s,
        t = 0.6 - x * x - y * y - z * z;
    int h = shuffle(int(ijk.x) + A[0], int(ijk.y) + A[1], int(ijk.z) + A[2]);
    A[a]++;
    if (t < 0.0)
        return 0.0;
    int b5 = h>>5 & 1, b4 = h>>4 & 1, b3 = h>>3 & 1, b2= h>>2 & 1, b = h & 3;
    float p = b==1?x:b==2?y:z, q = b==1?y:b==2?z:x, r = b==1?z:b==2?x:y;
    p = (b5==b3 ? -p : p); q = (b5==b4 ? -q : q); r = (b5!=(b4^b3) ? -r : r);
    t *= t;
    return 8.0 * t * t * (p + (b==0 ? q+r : b2==0 ? q : r));
}

float noise(float x, float y, float z)
{
    float s = (x + y + z) / 3.0;  
    vec3 ijk = vec3(int(floor(x+s)), int(floor(y+s)), int(floor(z+s)));
    s = float(ijk.x + ijk.y + ijk.z) / 6.0;
    vec3 uvw = vec3(x - float(ijk.x) + s, y - float(ijk.y) + s, z - float(ijk.z) + s);
    A[0] = A[1] = A[2] = 0;
    int hi = uvw.x >= uvw.z ? uvw.x >= uvw.y ? 0 : 1 : uvw.y >= uvw.z ? 1 : 2;
    int lo = uvw.x <  uvw.z ? uvw.x <  uvw.y ? 0 : 1 : uvw.y <  uvw.z ? 1 : 2;
    return K(hi, uvw, ijk) + K(3 - hi - lo, uvw, ijk) + K(lo, uvw, ijk) + K(0, uvw, ijk);
}

I translated it from Appendix B from Chapter 2 of Ken Perlin's Noise Hardware at this source:

https://www.csee.umbc.edu/~olano/s2002c36/ch02.pdf

Here is a public shade I did on Shader Toy that uses the posted noise function:

https://www.shadertoy.com/view/3slXzM

Some other good sources I found on the subject of noise during my research include:

https://thebookofshaders.com/11/

https://mzucker.github.io/html/perlin-noise-math-faq.html

https://rmarcus.info/blog/2018/03/04/perlin-noise.html

http://flafla2.github.io/2014/08/09/perlinnoise.html

https://mrl.nyu.edu/~perlin/noise/

https://rmarcus.info/blog/assets/perlin/perlin_paper.pdf

https://developer.nvidia.com/gpugems/GPUGems/gpugems_ch05.html

I highly recommend the book of shaders as it not only provides a great interactive explanation of noise, but other shader concepts as well.

EDIT:

Might be able to optimize the translated code by using some of the hardware-accelerated functions available in GLSL. Will update this post if I end up doing this.

Revert

also, I am pretty sure that Perlin/Simplex Noise is still pseudo random. From what I recall, the interesting thing is that you can layer and "zoom" the noise at different levels to make it seems very seamless. Don't quote me on that, but something to think about. – Revert

@Zibri Unfortunately, I am not super familiar with straight C or .sh commands. But it looks like the function is simply a pseudo-random number generator and not a noise function. Also keep in mind that glsl pixel shaders run directly on the gpu. You will not have access to any of those extra libraries or CPU capabilities that might be available in C. – Revert

The Book Of Shaders has a great explanation on how Simplex Noise is a more efficient version of Perlin Noise due to skewing the grid and less necessary calculations per point. Definitely worth the read. – Revert

also see the chapters on fractal brownian motion and voronoise – Revert

Andrew Meservy: no libraries needed... my noise function is very simple: 2 64 bit ints are the state x(n) and x(n-1).the simple and fast formula is x(n+1) = ROTR(x(n)+x(n-1),8). if you clone my git and run it you will see it in action. – Disproof

Answer 12

lygia, a multi-language shader library

If you don't want to copy / paste the functions into your shader, you can also use lygia, a multi-language shader library. It contains a few generative functions like cnoise, fbm, noised, pnoise, random, snoise in both GLSL and HLSL. And many other awesome functions as well. For this to work it:

Relays on #include "file" which is defined by Khronos GLSL standard and suported by most engines and enviroments (like glslViewer, glsl-canvas VS Code pluging, Unity, etc. ).

Example: cnoise

Using cnoise.glsl with #include:

#ifdef GL_ES
precision mediump float;
#endif

uniform vec2 u_resolution;
uniform float u_time;

#include "lygia/generative/cnoise.glsl"

void main (void) {
    vec2 st = gl_FragCoord.xy / u_resolution.xy;
    vec3 color = vec3(cnoise(vec3(st * 5.0, u_time)));

    gl_FragColor = vec4(color, 1.0);
}

To run this example I used glslViewer.

Gabrielson

Answer 13

Please see below an example how to add white noise to the rendered texture. The solution is to use two textures: original and pure white noise, like this one: wiki white noise

private static final String VERTEX_SHADER =
    "uniform mat4 uMVPMatrix;\n" +
    "uniform mat4 uMVMatrix;\n" +
    "uniform mat4 uSTMatrix;\n" +
    "attribute vec4 aPosition;\n" +
    "attribute vec4 aTextureCoord;\n" +
    "varying vec2 vTextureCoord;\n" +
    "varying vec4 vInCamPosition;\n" +
    "void main() {\n" +
    "    vTextureCoord = (uSTMatrix * aTextureCoord).xy;\n" +
    "    gl_Position = uMVPMatrix * aPosition;\n" +
    "}\n";

private static final String FRAGMENT_SHADER =
        "precision mediump float;\n" +
        "uniform sampler2D sTextureUnit;\n" +
        "uniform sampler2D sNoiseTextureUnit;\n" +
        "uniform float uNoseFactor;\n" +
        "varying vec2 vTextureCoord;\n" +
        "varying vec4 vInCamPosition;\n" +
        "void main() {\n" +
                "    gl_FragColor = texture2D(sTextureUnit, vTextureCoord);\n" +
                "    vec4 vRandChosenColor = texture2D(sNoiseTextureUnit, fract(vTextureCoord + uNoseFactor));\n" +
                "    gl_FragColor.r += (0.05 * vRandChosenColor.r);\n" +
                "    gl_FragColor.g += (0.05 * vRandChosenColor.g);\n" +
                "    gl_FragColor.b += (0.05 * vRandChosenColor.b);\n" +
        "}\n";

The fragment shared contains parameter uNoiseFactor which is updated on every rendering by main application:

float noiseValue = (float)(mRand.nextInt() % 1000)/1000;
int noiseFactorUniformHandle = GLES20.glGetUniformLocation( mProgram, "sNoiseTextureUnit");
GLES20.glUniform1f(noiseFactorUniformHandle, noiseFactor);

Catadromous

Answer 14

FWIW I had the same questions and I needed it to be implemented in WebGL 1.0, so I couldn't use a few of the examples given in previous answers. I tried the Gold Noise mentioned before, but the use of PHI doesn't really click for me. (distance(xy * PHI, xy) * seed just equals length(xy) * (1.0 - PHI) * seed so I don't see how the magic of PHI should be put to work when it gets directly multiplied by seed?

Anyway, I did something similar just without PHI and instead added some variation at another place, basically I take the tan of the distance between xy and some random point lying outside of the frame to the top right and then multiply with the distance between xy and another such random point lying in the bottom left (so there is no accidental match between these points). Looks pretty decent as far as I can see. Click to generate new frames.

(function main() {
  const dim = [512, 512];
  twgl.setDefaults({ attribPrefix: "a_" });
  const gl = twgl.getContext(document.querySelector("canvas"));
  gl.canvas.width = dim[0];
  gl.canvas.height = dim[1];
  const bfi = twgl.primitives.createXYQuadBufferInfo(gl);
  const pgi = twgl.createProgramInfo(gl, ["vs", "fs"]);
  gl.canvas.onclick = (() => {
    twgl.bindFramebufferInfo(gl, null);
    gl.useProgram(pgi.program);
    twgl.setUniforms(pgi, {
      u_resolution: dim,
      u_seed: Array(4).fill().map(Math.random)
    });
    twgl.setBuffersAndAttributes(gl, pgi, bfi);
    twgl.drawBufferInfo(gl, bfi);
  });
})();

<script src="https://twgljs.org/dist/4.x/twgl-full.min.js"></script>
<script id="vs" type="x-shader/x-vertex">
  attribute vec4 a_position;
  attribute vec2 a_texcoord;

  void main() {
    gl_Position = a_position;
  }
</script>
<script id="fs" type="x-shader/x-fragment">
  precision highp float;

  uniform vec2 u_resolution;
  uniform vec2 u_seed[2];
  
  void main() {
    float uni = fract(
      tan(distance(
        gl_FragCoord.xy,
        u_resolution * (u_seed[0] + 1.0)
      )) * distance(
        gl_FragCoord.xy,
        u_resolution * (u_seed[1] - 2.0)
      )
    );
    gl_FragColor = vec4(uni, uni, uni, 1.0);
  }
</script>
<canvas></canvas>

Howenstein