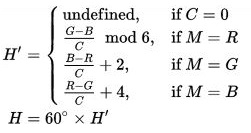RGB to HSL conversion

Question

I'm creating a Color Picker tool and for the HSL slider, I need to be able to convert RGB to HSL. When I searched SO for a way to do the conversion, I found this question HSL to RGB color conversion.

While it provides a function to do conversion from RGB to HSL, I see no explanation to what's really going on in the calculation. To understand it better, I've read the HSL and HSV on Wikipedia.

Later, I've rewritten the function from the "HSL to RGB color conversion" using the calculations from the "HSL and HSV" page.

I'm stuck at the calculation of hue if the R is the max value. See the calculation from the "HSL and HSV" page:

This is from another wiki page that's in Dutch:

and this is from the answers to "HSL to RGB color conversion":

case r: h = (g - b) / d + (g < b ? 6 : 0); break; // d = max-min = c

I've tested all three with a few RGB values and they seem to produce similar (if not exact) results. What I'm wondering is are they performing the same thing? Will get I different results for some specific RGB values? Which one should I be using?

hue = (g - b) / c;                   // dutch wiki
hue = ((g - b) / c) % 6;             // eng wiki
hue = (g - b) / c + (g < b ? 6 : 0); // SO answer

function rgb2hsl(r, g, b) {
    // see https://en.wikipedia.org/wiki/HSL_and_HSV#Formal_derivation
    // convert r,g,b [0,255] range to [0,1]
    r = r / 255,
    g = g / 255,
    b = b / 255;
    // get the min and max of r,g,b
    var max = Math.max(r, g, b);
    var min = Math.min(r, g, b);
    // lightness is the average of the largest and smallest color components
    var lum = (max + min) / 2;
    var hue;
    var sat;
    if (max == min) { // no saturation
        hue = 0;
        sat = 0;
    } else {
        var c = max - min; // chroma
        // saturation is simply the chroma scaled to fill
        // the interval [0, 1] for every combination of hue and lightness
        sat = c / (1 - Math.abs(2 * lum - 1));
        switch(max) {
            case r:
                // hue = (g - b) / c;
                // hue = ((g - b) / c) % 6;
                // hue = (g - b) / c + (g < b ? 6 : 0);
                break;
            case g:
                hue = (b - r) / c + 2;
                break;
            case b:
                hue = (r - g) / c + 4;
                break;
        }
    }
    hue = Math.round(hue * 60); // °
    sat = Math.round(sat * 100); // %
    lum = Math.round(lum * 100); // %
    return [hue, sat, lum];
}

Sorry

The English one looks correct to me, the Dutch one I don't recognise and I don't understand what it says on the wiki page. :) – Romanticize

Here's the octave implementation of hsv2rgb: hg.savannah.gnu.org/hgweb/octave/file/549f8625a61b/scripts/… – Prior

Answer 1

I've been reading several wiki pages and checking different calculations, and creating visualizations of RGB cube projection onto a hexagon. And I'd like to post my understanding of this conversion. Since I find this conversion (representations of color models using geometric shapes) interesting, I'll try to be as thorough as I can be. First, let's start with RGB.

RGB

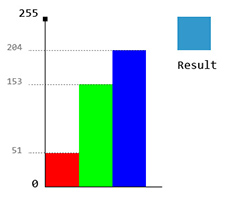
Well, this doesn't really need much explanation. In its simplest form, you have 3 values, R, G, and B in the range of [0,255]. For example, 51,153,204. We can represent it using a bar graph:

RGB Cube

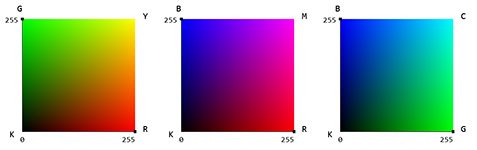
We can also represent a color in a 3D space. We have three values R, G, B that corresponds to X, Y, and Z. All three values are in the [0,255] range, which results in a cube. But before creating the RGB cube, let's work on 2D space first. Two combinations of R,G,B gives us: RG, RB, GB. If we were to graph these on a plane, we'd get the following:

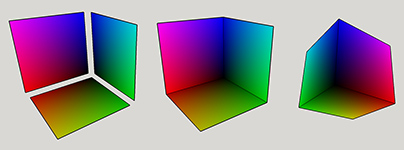
These are the first three sides of the RGB cube. If we place them on a 3D space, it results in a half cube:

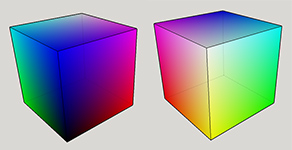
If you check the above graph, by mixing two colors, we get a new color at (255,255), and these are Yellow, Magenta, and Cyan. Again, two combinations of these gives us: YM, YC, and MC. These are the missing sides of the cube. Once we add them, we get a complete cube:

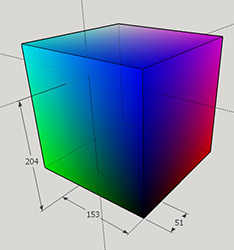
And the position of 51,153,204 in this cube:

Projection of RGB Cube onto a hexagon

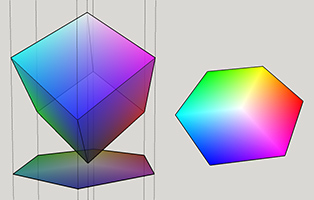
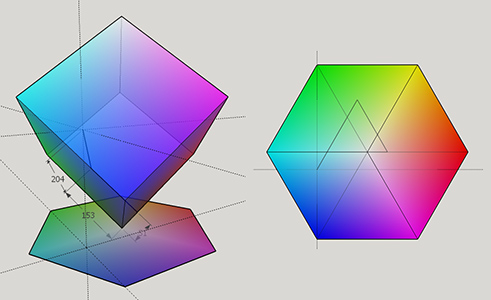
Now that we have the RGB Cube, let's project it onto a hexagon. First, we tilt the cube by 45° on the x, and then 35.264° on the y. After the second tilt, black corner is at the bottom and the white corner is at the top, and they both pass through the z axis.

As you can see, we get the hexagon look we want with the correct hue order when we look at the cube from the top. But we need to project this onto a real hexagon. What we do is draw a hexagon that is in the same size with the cube top view. All the corners of the hexagon corresponds to the corners of the cube and the colors, and the top corner of the cube that is white, is projected onto the center of the hexagon. Black is omitted. And if we map every color onto the hexagon, we get the look at right.

And the position of 51,153,204 on the hexagon would be:

Calculating the Hue

Before we make the calculation, let's define what hue is.

Hue is roughly the angle of the vector to a point in the projection, with red at 0°.

... hue is how far around that hexagon’s edge the point lies.

This is the calculation from the HSL and HSV wiki page. We'll be using it in this explanation.

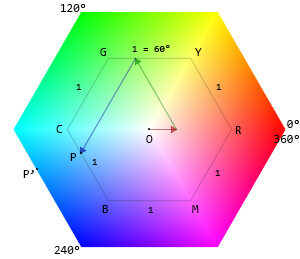
Examine the hexagon and the position of 51,153,204 on it.

First, we scale the R, G, B values to fill the [0,1] interval.

R = R / 255    R =  51 / 255 = 0.2
G = G / 255    G = 153 / 255 = 0.6
B = B / 255    B = 204 / 255 = 0.8

Next, find the max and min values of R, G, B

M = max(R, G, B)    M = max(0.2, 0.6, 0.8) = 0.8
m = min(R, G, B)    m = min(0.2, 0.6, 0.8) = 0.2

Then, calculate C (chroma). Chroma is defined as:

... chroma is roughly the distance of the point from the origin.

Chroma is the relative size of the hexagon passing through a point ...

C = OP / OP'
C = M - m
C = 0.8- 0.2 = 0.6

Now, we have the R, G, B, and C values. If we check the conditions, if M = B returns true for 51,153,204. So, we'll be using H'= (R - G) / C + 4.

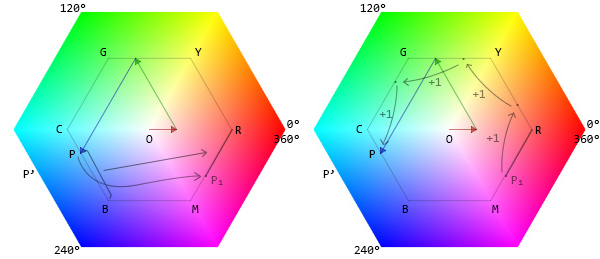
Let's check the hexagon again. (R - G) / C gives us the length of BP segment.

segment = (R - G) / C = (0.2 - 0.6) / 0.6 = -0.6666666666666666

We'll place this segment on the inner hexagon. Starting point of the hexagon is R (red) at 0°. If the segment length is positive, it should be on RY, if negative, it should be on RM. In this case, it is negative -0.6666666666666666, and is on the RM edge.

Next, we need to shift the position of the segment, or rather P₁ towars the B (because M = B). Blue is at 240°. Hexagon has 6 sides. Each side corresponds to 60°. 240 / 60 = 4. We need to shift (increment) the P₁ by 4 (which is 240°). After the shift, P₁ will be at P and we'll get the length of RYGCP.

segment = (R - G) / C = (0.2 - 0.6) / 0.6 = -0.6666666666666666
RYGCP   = segment + 4 = 3.3333333333333335

Circumference of the hexagon is 6 which corresponds to 360°. 53,151,204's distance to 0° is 3.3333333333333335. If we multiply 3.3333333333333335 by 60, we'll get its position in degrees.

H' = 3.3333333333333335
H  = H' * 60 = 200°

---

In the case of if M = R, since we place one end of the segment at R (0°), we don't need to shift the segment to R if the segment length is positive. The position of P₁ will be positive. But if the segment length is negative, we need to shift it by 6, because negative value means that the angular position is greater than 180° and we need to do a full rotation.

So, neither the Dutch wiki solution hue = (g - b) / c; nor the Eng wiki solution hue = ((g - b) / c) % 6; will work for negative segment length. Only the SO answer hue = (g - b) / c + (g < b ? 6 : 0); works for both negative and positive values.

JSFiddle: Test all three methods for rgb(255,71,99)

---

JSFiddle: Find a color's position in RGB Cube and hue hexagon visually

Working hue calculation:

console.log(rgb2hue(51,153,204));
console.log(rgb2hue(255,71,99));
console.log(rgb2hue(255,0,0));
console.log(rgb2hue(255,128,0));
console.log(rgb2hue(124,252,0));

function rgb2hue(r, g, b) {
  r /= 255;
  g /= 255;
  b /= 255;
  var max = Math.max(r, g, b);
  var min = Math.min(r, g, b);
  var c   = max - min;
  var hue;
  if (c == 0) {
    hue = 0;
  } else {
    switch(max) {
      case r:
        var segment = (g - b) / c;
        var shift   = 0 / 60;       // R° / (360° / hex sides)
        if (segment < 0) {          // hue > 180, full rotation
          shift = 360 / 60;         // R° / (360° / hex sides)
        }
        hue = segment + shift;
        break;
      case g:
        var segment = (b - r) / c;
        var shift   = 120 / 60;     // G° / (360° / hex sides)
        hue = segment + shift;
        break;
      case b:
        var segment = (r - g) / c;
        var shift   = 240 / 60;     // B° / (360° / hex sides)
        hue = segment + shift;
        break;
    }
  }
  return hue * 60; // hue is in [0,6], scale it up
}

Sorry

Hi, I am shocked that you answer is ignored or not seen by majority. Thank you so much for explanation I have been researching it for a while and your answer is the best – Cussedness

@AlexanderGurevich I just love to get to the bottom of things, and this was a good study. I wanted to put it out in the open. I'm glad someone have found it useful :) – Sorry

Wow, amazing answer! I would upvote it more than once if that would be possible :D – Phobia

Are we working with RGB as-is? or do we need to linearize it first? – Irritation

Still in 2021, this is so wonderful. Thank you for your work. – Photoemission

Awesome auto-answering, thanks for the effort. For the sake of completeness, you could perhaps provide the final rgb2hsl :) – Coca

@Coca You can check the one rgb2hsl in the question. All three hue calculations (for M=R) are there. Just delete the first two. – Sorry

I do not follow the logic here. You project the cube onto a hexagon, but that only gives you a certain amount of colors. My idea was to transform the cube into a hexagonal grid and come up with a formula for that. Not saying your wrong just not sure if all the colors are there. – Hephaestus

@Sorry Why wouldn't the Eng wiki solution (hue = ((g - b) / c) % 6) work for negative segment lengths? The % 6 modulo operation would do exactly the same as + (g < b ? 6 : 0). – Luteal

@LeadVaxeral I think you're mistaken about my question/answer. This is not really about 3D projection. It's about calculating the hue. This does not require 3D. If you want to create a 3D space that contains all colors, you simply use the cube or modify/reshape it. That is out of scope of this post. – Sorry

@Luteal It simply doesn't. See the "test all three methods" link in my answer. Also check Matey's answer (and the comments). – Sorry

I'd also like to mention that in places where hue = ((g - b) / c) % 6 seem to work, the actual calculation is seperated into two. The hue is later corrected (for negative values) with if (h < 0) h += 360;. For example, examine Crashalot's answer. So saying hue = ((g - b) / c) % 6 works is misleading. It's incomplete. That's what got me in the first place. Wiki pages do not seem to mention this. – Sorry

@Sorry I think it depends on the programming language used, and its definition of the modulo operator. In most programming languages, % 6 will ensure a positive result, effectively adding 6 (as many times as needed) when g - b is negative. That is definitely the case in python for example, and the Eng wiki and SO codes are then strictly identical. – Luteal

@Luteal Oh, right. Indeed that seems to be the case with Python. In JavaScript, however, % doesn't handle negative values. So one needs to manually adjust the result. Thanks for point it out. – Sorry

Answer 2

This page provides a function for conversion between color spaces, including RGB to HSL.

function RGBToHSL(r,g,b) {
  // Make r, g, and b fractions of 1
  r /= 255;
  g /= 255;
  b /= 255;

  // Find greatest and smallest channel values
  let cmin = Math.min(r,g,b),
      cmax = Math.max(r,g,b),
      delta = cmax - cmin,
      h = 0,
      s = 0,
      l = 0;

  // Calculate hue
  // No difference
  if (delta === 0)
    h = 0;
  // Red is max
  else if (cmax === r)
    h = ((g - b) / delta) % 6;
  // Green is max
  else if (cmax === g)
    h = (b - r) / delta + 2;
  // Blue is max
  else
    h = (r - g) / delta + 4;

  h = Math.round(h * 60);
    
  // Make negative hues positive behind 360°
  if (h < 0)
      h += 360;

  // Calculate lightness
  l = (cmax + cmin) / 2;

  // Calculate saturation
  s = delta === 0 ? 0 : delta / (1 - Math.abs(2 * l - 1));
    
  // Multiply l and s by 100
  s = +(s * 100).toFixed(1);
  l = +(l * 100).toFixed(1);

  return "hsl(" + h + "," + s + "%," + l + "%)";
}

Hollingshead

The code on line 3, 4 and 5 is not making fractions of 1. It's scaling the number into a ratio. If anything, it would be calculating the fraction of 255. – Dig

Answer 3

Continuing from my comment, the English version looks correct, but I'm not sure what's happening in the Dutch version as I don't understand the WIKI page.

Here is an ES6 version that I made from the English WIKI page, along with some sample data that appear to match the WIKI examples (give or take Javascript's numeric accuracy). Hopefully it may be of use while creating your own function.

// see: https://en.wikipedia.org/wiki/RGB_color_model
// see: https://en.wikipedia.org/wiki/HSL_and_HSV

// expects R, G, B, Cmax and chroma to be in number interval [0, 1]
// returns undefined if chroma is 0, or a number interval [0, 360] degrees
function hue(R, G, B, Cmax, chroma) {
  let H;
  if (chroma === 0) {
    return H;
  }
  if (Cmax === R) {
    H = ((G - B) / chroma) % 6;
  } else if (Cmax === G) {
    H = ((B - R) / chroma) + 2;
  } else if (Cmax === B) {
    H = ((R - G) / chroma) + 4;
  }
  H *= 60;
  return H < 0 ? H + 360 : H;
}

// returns the average of the supplied number arguments
function average(...theArgs) {
  return theArgs.length ? theArgs.reduce((p, c) => p + c, 0) / theArgs.length : 0;
}

// expects R, G, B, Cmin, Cmax and chroma to be in number interval [0, 1]
// type is by default 'bi-hexcone' equation
// set 'luma601' or 'luma709' for alternatives
// see: https://en.wikipedia.org/wiki/Luma_(video)
// returns a number interval [0, 1]
function lightness(R, G, B, Cmin, Cmax, type = 'bi-hexcone') {
  if (type === 'luma601') {
    return (0.299 * R) + (0.587 * G) + (0.114 * B);
  }
  if (type === 'luma709') {
    return (0.2126 * R) + (0.7152 * G) + (0.0772 * B);
  }
  return average(Cmin, Cmax);
}

// expects L and chroma to be in number interval [0, 1]
// returns a number interval [0, 1]
function saturation(L, chroma) {
  return chroma === 0 ? 0 : chroma / (1 - Math.abs(2 * L - 1));
}

// returns the value to a fixed number of digits
function toFixed(value, digits) {
  return Number.isFinite(value) && Number.isFinite(digits) ? value.toFixed(digits) : value;
}

// expects R, G, and B to be in number interval [0, 1]
// returns a Map of H, S and L in the appropriate interval and digits
function RGB2HSL(R, G, B, fixed = true) {
  const Cmin = Math.min(R, G, B);
  const Cmax = Math.max(R, G, B);
  const chroma = Cmax - Cmin;
  // default 'bi-hexcone' equation
  const L = lightness(R, G, B, Cmin, Cmax);
  // H in degrees interval [0, 360]
  // L and S in interval [0, 1]
  return new Map([
    ['H', toFixed(hue(R, G, B, Cmax, chroma), fixed && 1)],
    ['S', toFixed(saturation(L, chroma), fixed && 3)],
    ['L', toFixed(L, fixed && 3)]
  ]);
}

// expects value to be number in interval [0, 255]
// returns normalised value as a number interval [0, 1]
function colourRange(value) {
  return value / 255;
};

// expects R, G, and B to be in number interval [0, 255]
function RGBdec2HSL(R, G, B) {
  return RGB2HSL(colourRange(R), colourRange(G), colourRange(B));
}

// converts a hexidecimal string into a decimal number
function hex2dec(value) {
  return parseInt(value, 16);
}

// slices a string into an array of paired characters
function pairSlicer(value) {
  return value.match(/../g);
}

// prepend '0's to the start of a string and make specific length
function prePad(value, count) {
  return ('0'.repeat(count) + value).slice(-count);
}

// format hex pair string from value
function hexPair(value) {
  return hex2dec(prePad(value, 2));
}

// expects R, G, and B to be hex string in interval ['00', 'FF']
// without a leading '#' character
function RGBhex2HSL(R, G, B) {
  return RGBdec2HSL(hexPair(R), hexPair(G), hexPair(B));
}

// expects RGB to be a hex string in interval ['000000', 'FFFFFF']
// with or without a leading '#' character
function RGBstr2HSL(RGB) {
  const hex = prePad(RGB.charAt(0) === '#' ? RGB.slice(1) : RGB, 6);
  return RGBhex2HSL(...pairSlicer(hex).slice(0, 3));
}

// expects value to be a Map object
function logIt(value) {
  console.log(value);
  document.getElementById('out').textContent += JSON.stringify([...value]) + '\n';
};

logIt(RGBstr2HSL('000000'));
logIt(RGBstr2HSL('#808080'));
logIt(RGB2HSL(0, 0, 0));
logIt(RGB2HSL(1, 1, 1));
logIt(RGBdec2HSL(0, 0, 0));
logIt(RGBdec2HSL(255, 255, 254));
logIt(RGBhex2HSL('BF', 'BF', '00'));
logIt(RGBstr2HSL('008000'));
logIt(RGBstr2HSL('80FFFF'));
logIt(RGBstr2HSL('8080FF'));
logIt(RGBstr2HSL('BF40BF'));
logIt(RGBstr2HSL('A0A424'));
logIt(RGBstr2HSL('411BEA'));
logIt(RGBstr2HSL('1EAC41'));
logIt(RGBstr2HSL('F0C80E'));
logIt(RGBstr2HSL('B430E5'));
logIt(RGBstr2HSL('ED7651'));
logIt(RGBstr2HSL('FEF888'));
logIt(RGBstr2HSL('19CB97'));
logIt(RGBstr2HSL('362698'));
logIt(RGBstr2HSL('7E7EB8'));

<pre id="out"></pre>

Romanticize

I really appreciate the effort, but this seems much more complicated than the one I've already written :) I've been reading the wiki pages over and over again, and creating the rgb cube-to-hexagon projection in a 3d software. I'm really close to understanding everything in the calculation. I'll post my understanding sometime soon. (Sorry for the late reply :) – Sorry

I don't know about much more complicated (sure, in all it can do a few more things than your example), but basically it's the same but broken down into smaller testable and reusable functions rather than a single function. I could probably do it in a single line of code, but that wouldn't be very readable, reusable or maintainable. Oh and I used ES6 rather than just ES3, I know you didn't ask for any code but I needed to dust off some rust and I thought that I may as well share my tinkering with you in an answer rather than just the comment. :) – Romanticize

I've posted my answer (if you haven't seen it already). It's incomplete right now. Updated it once. Gonna update it again. I'd like your feedback (I might be doing it wrong, idk :) – Sorry

It's a very pretty description of what needs to be calculated, but so far doesn't answer the actual question that you posted. I'm kind of thinking that perhaps your questions and answer were better suited to mathoverflow.net as it doesn't really seem to have much to do with the programming aspect, but a great deal to do with mathematics. – Romanticize

It's still not done yet. I'll add the last part where I'll talk about the calculation. I liked this conversion thing so much that I wanted to be thorough with it. I'm sure it'll be useful for future visitors. – Sorry

I just finished updating my answer and noticed that hue = ((g - b) / c) % 6; results in incorrect values. It doesn't handle negative values. Also I don't see any scenario where (g - b) / c) is greater than 6. It should always be <= 1. So why do mod? See this fiddle test. – Sorry

In my answer you will see a check for the negative, and add 360. I haven't looked so close at the theory or the math, I have just assumed that it is correct as I have seen it in several sources and the numbers come out as expected. – Romanticize

Answer 4

Hue in HSL is like an angle in a circle. Relevant values for such angle reside in the 0..360 interval. However, negative values might come out of the calculation. And that's why those three formulas are different. They do the same in the end, they just handle differently the values outside the 0..360 interval. Or, to be precise, the 0..6 interval which is then eventually multiplied by 60 to 0..360

hue = (g - b) / c; // dutch wiki does nothing with negative values and presumes the subsequent code can handle negative H values.

hue = ((g - b) / c) % 6; // eng wiki uses the % operator to fit the values inside the 0..6 interval

hue = (g - b) / c + (g < b ? 6 : 0); // SO answer takes care of negative values by adding +6 to make them positive

You see that these are just cosmetic differences. Either the second or the third formula will work fine for you.

Monicamonie

I don't think the second will work for both positive and negative values. I don't see any scenario where (g - b) / c) is greater than 6. It should always be <= 1. So mod seems redundant. Only the third formula works as expected. See my updated answer. – Sorry

@Sorry : mod for negative values of the dividend increases the dividend by the divisor until it's positive. Which is exactly the same as the third formula. – Monicamonie

See this jsfiddle. en_rgb2hue() uses the mod calculation. It does not give the correct value. – Sorry

My bad. There are obviously two worlds regarding how the negative values should be handled by %. Thanks for correcting me. – Monicamonie