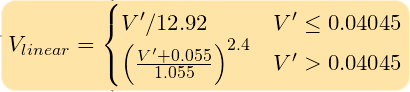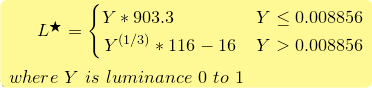Formula to determine perceived brightness of RGB color

Question

I'm looking for some kind of formula or algorithm to determine the brightness of a color given the RGB values. I know it can't be as simple as adding the RGB values together and having higher sums be brighter, but I'm kind of at a loss as to where to start.

Gerrilee

Perceived brightness is what I think I'm looking for, thank you. – Gerrilee

I found [this code][1] (written in C#) that does an excellent job of calculating the "brightness" of a color. In this scenario, the code is trying to determine whether to put white or black text over the color. [1]:nbdtech.com/Blog/archive/2008/04/27/… – Undenominational

There is a good article (Manipulating colors in .NET - Part 1) about color spaces and conversations between them including both theory and the code (C#). For the answer look at Conversion between models topic in the article. – Swallowtail

See my answer, but really simple is: brightness = 0.2*r + 0.7*g + 0.1*b – Anny

Answer 1

The method could vary depending on your needs. Here are 3 ways to calculate Luminance:

• Luminance (standard for certain colour spaces): (0.2126*R + 0.7152*G + 0.0722*B) source

• Luminance (perceived option 1): (0.299*R + 0.587*G + 0.114*B) source

• Luminance (perceived option 2, slower to calculate): sqrt( 0.241*R^2 + 0.691*G^2 + 0.068*B^2 ) → sqrt( 0.299*R^2 + 0.587*G^2 + 0.114*B^2 ) (thanks to @MatthewHerbst) source

^{_{[Edit: added examples using named css colors sorted with each method.]}}

Cannonball

Note that both of these emphasize the physiological aspects: the human eyeball is most sensitive to green light, less to red and least to blue. – Mcconnell

Note also that all of these are probably for linear 0-1 RGB, and you probably have gamma-corrected 0-255 RGB. They are not converted like you think they are. – Phyllode

For the first two the source is in the other answers. As for the final one - I think it was from the lectures on television or graphics... – Cannonball

I think your last formula is incorrect. I get it returning black for a dark blue color. – Savannasavannah

Not correct. Before applying the linear transformation, one must first apply the inverse of the gamma function for the color space. Then after applying the linear function, the gamma function is applied. – Scammony

Luminance only accounts for human spectral sensitivity. It does not account the for the human non-linear perception of Luminance, which the CIE have standardised as "Lightness" (the L in the CIELAB color space) Depending on your application you may need to first calculate Luminance, and then Lightness ... en.wikipedia.org/wiki/Lightness – Commissionaire

The first two are linear, the last one is a bit arbitrary and does not incorporate gamma correction or sRGB color space correction. – Pinson

@alexstrange the first formula uses linear RGB values and the second uses gamma-corrected values. The first formula is more modern, the second dates from the invention of NTSC. And the range doesn't matter since there are no non-linear operations. The third formula appears to operate on gamma-corrected values, but as it isn't a standard it's harder to be sure. – Jettiejettison

If the color components are limited to 8 bits, the perceived luminance option 2 can be calculated as fast as the option 1 with a 256 ints lookup table of the precomputed squares. And all three can be calculated really fast with a lookup table of each color value premultiplied with each coefficient. Though that does require a lot of memory. – Blither

In the last formula, is it (0.299*R)^2 or is it 0.299*(R^2) ? – Lohr

Here's a jsfiddle that lets you pick colors and see the luminance, in case anybody else needs to see what kinds of values you get from these formulas. (Based on the last slowest formula) jsfiddle.net/sbrexep0 – Boor

@KaizerSozay As it's written here it would mean 0.299*(R^2) (because exponentiation goes before multiplication) – Musgrove

@bobobobo From the Wikipedia pages for en.wikipedia.org/wiki/Relative_luminance and en.wikipedia.org/wiki/Grayscale . It's important to note that the R, G, & B multipliers are not based on any exact science; rather, they're just values that have been found to be the average luma perceived by the human eye for each channel. This was crucially important when there existed both B&W (grayscale) & color TV sets; the testing of the population was done around that time (1950s). More background at en.wikipedia.org/wiki/Color_television . – Peppie

When it comes to W3C on a11y, the newer WCAG guide specifies the 1st formula with suggestion for linearization: w3.org/TR/WCAG20-TECHS/G17.html#G17-tests – Olvan

@MarkRansom I have verified that the last uses gamma-corrected values. FWIW to my eye the first formula gives the best results, though it's expensive if your colors aren't in linear space. The last could be a nice hack if you don't want to undo the gamma. – Durward

@Durward formula #3 has been modified, now it's the same as #2 with an approximation of gamma to linear conversion. It's using a gamma of 2.0 instead of 2.2 to make things quicker. If you're going to use linear RGB I'd use the constants from formula #1 instead, my experience matches yours that #1 with linear is the best. – Jettiejettison

As I state in my separate answer, the math in this answer is generally incorrect and incomplete. #1 requires linearized sRGB which is not shown. #2 is for YCC NTSC and not sRGB. #3 is generally wrong in a lot of ways, but oddly was "more correct" before someone edited it to make it less correct! #3 is "sort of like L*" lightness, but not quite. The struck out version is ~5% incorrect, the M.Ransom version is ~15% incorrect and #1, #2 are ~40% incorrect if referenced to perceptual lightness (L*). None of these find luminance (Y), and none find perceptual brightness (Q). – Chantry

@MarkRansom — Good point about gamma-encoded values. However, it's assuming a gamma of 2.0 instead of the usual 2.2. So a better formula would be (0.299*R^2.2 + 0.587*G^2.2 + 0.114*B^2.2) ^ (1/2.2). – Irritant

@ToddLehman no doubt 2.2 and its inverse would be more accurate than 2.0 and sqrt. But often when you're dealing with pixels every microsecond counts, and squares and sqrt are a lot faster than taking an arbitrary power - and the visual difference is probably barely noticeable. – Jettiejettison

@MarkRansom — Indeed, sometimes speed matters. :) Interestingly, even a 10th-order Maclauren series expansion of x^(1/2.2) is only accurate for x>0.2 and requires 29 floating-point operations. So that's probably a lot slower than a modern hardware square root operation. But then again, speed doesn't always matter; sometimes accuracy is more important. – Irritant

Answer 2

I think what you are looking for is the RGB -> Luma conversion formula.

Photometric/digital ITU BT.709:

Y = 0.2126 R + 0.7152 G + 0.0722 B

Digital ITU BT.601 (gives more weight to the R and B components):

Y = 0.299 R + 0.587 G + 0.114 B

If you are willing to trade accuracy for perfomance, there are two approximation formulas for this one:

Y = 0.33 R + 0.5 G + 0.16 B

Y = 0.375 R + 0.5 G + 0.125 B

These can be calculated quickly as

Y = (R+R+B+G+G+G)/6

Y = (R+R+R+B+G+G+G+G)>>3

Blither

How come your 'calculated quickly' values don't include blue in the approximation at all? – Horsehair

@Jonathan Dumaine - the two quick calculation formulas both include blue - 1st one is (2*Red + Blue + 3*Green)/6, 2nd one is (3*Red + Blue + 4*Green)>>3. granted, in both quick approximations, Blue has the lowest weight, but it's still there. – Blither

The quick version is even faster if you do it as: Y = (R<<1+R+G<<2+B)>>3 (thats only 3-4 CPU cycles on ARM) but I guess a good compiler will do that optimisation for you. – Photovoltaic

@Photovoltaic I believe you are missing a few parenthesis, the addition operations will go first, so your code is the same as: Y = (R << (1 + R + G) << (2 + B)) >> 3. The correct snippet: int Y = ((R << 1) + R + (G << 2) + B) >> 3;. – Koval

Luma (Yʹ in otherwords Y prime) is not luminance (Y), and luma, while it is gamma compressed and may be useful for encoding image data, for later decoding, is not perceptually uniform especially for more saturated colors. As such, it is not a good metric for perceived lightness. Luminance is linear, and not perceptually uniform, and also not useful for predicting lightness perception. – Chantry

Answer 3

The "Accepted" Answer is Incorrect and Incomplete

The only answers that are accurate are the @jive-dadson and @EddingtonsMonkey answers, and in support @nils-pipenbrinck. The other answers (including the accepted) are linking to or citing sources that are either wrong, irrelevant, obsolete, or broken.

Briefly:

• sRGB must be LINEARIZED before applying the coefficients.
• Luminance (L or Y) is linearly additive as is light.
• Perceived lightness (L*) is nonlinear to light as is human perception.
• HSV and HSL are not even remotely accurate in terms of perception. (Not perceptually uniform).
• The IEC standard for sRGB specifies a threshold of 0.04045 it is NOT 0.03928 (that was from an obsolete early draft).
• To be useful (i.e. relative to perception), Euclidian distances require a perceptually uniform Cartesian vector space such as CIELAB. sRGB is not one.

---

What follows is a correct and complete answer:

Because this thread appears highly in search engines, I am adding this answer to clarify the various misconceptions on the subject.

Luminance is a linear measure of light, spectrally weighted for normal vision but not adjusted for the non-linear perception of lightness. It can be a relative measure, Y as in CIEXYZ, or as L, an absolute measure in cd/m² (not to be confused with L*).

Perceived lightness is used by some vision models such as CIELAB, here L* (Lstar) is a value of perceptual lightness, and is non-linear relative to light, to approximate the human vision non-linear response curve. (That is, linear to perception but therefore non-linear to light).

Brightness is a perceptual attribute, it does not have a "physical" measure. However some color appearance models do have a value, usually denoted as Q for perceived brightness, which is different than perceived lightness. Note: Brightness is not to be confused with luminous energy, which is also denoted with Q, but is not necessarily calculated the same as brightness for a given color appearance model.

Luma is a gamma encoded and spectrally weighted signal used in some video encodings (such as Y´I´Q´ or Y´U´V´). The prime symbol after the Y (Y´) indicates the data is gamma encoded. Luma is not to be confused with linear luminance (Y or L per above).

Weighting means the digital values for each of the red, green, or blue primary colors in a display are adjusted so that an equal value of red, green, and blue results in a neutral gray or white. This is defined in the given color space, such as BT.709. in other words, 255 blue is much darker than 255 green, in accordance with the luminous efficiency function.

Gamma or transfer curve (TRC) is a curve that is often similar to the perceptual curve, and is commonly applied to image data for storage or broadcast to reduce perceived noise and/or improve data utilization (and related reasons).

In the early days of electronic imaging, it was often referred to as Gamma Correction.

---

Solution: To estimate perceived lightness

(This assumes conditions close to the reference environment)

• First convert gamma encoded R´G´B´ image values to linear luminance ( Y ).
  • linearize each R´G´B´ value to linear RGB
  • apply the weighting coefficients to each R, G, B value.
  • sum the results to get Y.
• Then convert Y to non-linear perceived lightness (L*).

TO FIND LUMINANCE:

...Because apparently it was lost somewhere...

Step One:

Convert all sRGB 8 bit integer values to decimal 0.0-1.0

  vR = sR / 255;
  vG = sG / 255;
  vB = sB / 255;

Step Two:

Convert a gamma encoded RGB to a linear value. sRGB (computer standard) for instance requires a power curve of approximately V^2.2, though the "accurate" transform is:

Where V´ is the gamma-encoded R, G, or B channel of sRGB.
Pseudocode:

function sRGBtoLin(colorChannel) {
        // Send this function a decimal sRGB gamma encoded color value
        // between 0.0 and 1.0, and it returns a linearized value.

    if ( colorChannel <= 0.04045 ) {
            return colorChannel / 12.92;
        } else {
            return pow((( colorChannel + 0.055)/1.055),2.4);
        }
    }

Step Three:

To find Luminance (Y) apply the standard coefficients for sRGB:

Pseudocode using above functions:

Y = (0.2126 * sRGBtoLin(vR) + 0.7152 * sRGBtoLin(vG) + 0.0722 * sRGBtoLin(vB))

---

TO FIND PERCEIVED LIGHTNESS:

Step Four:

Take luminance Y from above, and transform to L*

Pseudocode:

function YtoLstar(Y) {
        // Send this function a luminance value between 0.0 and 1.0,
        // and it returns L* which is "perceptual lightness"

    if ( Y <= (216/24389)) {       // The CIE standard states 0.008856 but 216/24389 is the intent for 0.008856451679036
            return Y * (24389/27);  // The CIE standard states 903.3, but 24389/27 is the intent, making 903.296296296296296
        } else {
            return pow(Y,(1/3)) * 116 - 16;
        }
    }

L* is a value from 0 (black) to 100 (white) where 50 is the perceptual "middle grey". L* = 50 is the equivalent of Y = 18.4, or in other words an 18% grey card, representing the middle of a photographic exposure (Ansel Adams zone V).

---

2023 Edit:

Adds by Myndex in an effort toward completeness:

Some of the other answers on this page are showing the math for Luma (Yʹ in other words Y prime) and luma should never be confused with relative luminance (Y). And neither is perceptually uniform lightness nor brightness.

• Luma, while it is gamma compressed and may be useful for encoding image data for later decoding, is not perceptually uniform especially for more saturated colors. As such, Luma is generally not a good metric for perceived lightness.
• Luminance is linear per light, but not linear per perception, in other words, it is not perceptually uniform, and therefore not useful for predicting lightness perception.
• Lstar L* in my answer above is often used for predicting a perceived lightness. It is based on Munsell Value, which is derived from experiments in a specifically defined environment using large diffuse color samples.
  • L* is not particularly context sensitive, i.e. not sensitive to things like simultaneous contrast, HK, or other contextual sensations.
  • Therefore, L* can only take us part way to an accurate model of perceived lightness.
  • L* along with CIELAB is good for determining "small differences" between two items, i.e. close to the "Just Noticeable Difference" (JND threshold).
    • L* becomes less accurate at larger supra-threshold levels and large differences, where other contextual factors begin to have a more substantial effect.
    • Supra-threshold curve shapes are different than the JND threshold curve.
  • L* puts perceptual middle grey at 18%.
    • Actual perceived middle grey depends on context.
    • Middle contrast for high spatial frequency stimuli (such as text) is often much higher than 18%.
    • Contrast perception is more complicated than the difference between two lightness values, and simple difference or ratios are of limited utility, and not uniform over the visual range.

Additional References:

IEC 61966-2-1:1999 Standard
sRGB
CIELAB
CIEXYZ
Charles Poynton's Gamma FAQ

Reference links in the above text:

Luminance
Lightness
Lightness vs Brightness at CIE
Luminous energy
Luma
YIQ
YUV and others in the book Video Demystified
Rec._709
Luminous efficiency function
Gamma correction

Chantry

I created a demonstration comparing BT.601 Luma and CIE 1976 L* Perceptual Gray, using few MATLAB commands: Luma=rgb2gray(RGB);LAB=rgb2lab(RGB);LAB(:,:,2:3)=0;PerceptualGray=lab2rgb(LAB); – Sheepfold

@asdfasdfads Yes, L*a*b* does not take into account a number of psychophysical attributes. Helmholtz-Kohlrausch effect is one, but there are many others. CIELAB is not a "full" image assessment model by any means. In my post I was trying to cover the basic concepts as completely as possible without venturing into the very deep minutiae. The Hunt model, Fairchild's models, and others do a more complete job, but are also substantially more complex. – Chantry

Note that the incorrect threshold from the old sRGB standard is propagated in other publications, including the official description of the minimum text contrast test from Web Content Accessibility Guidelines 2.1. Since accessibility may have motivated the question, that may be useful information. w3.org/WAI/WCAG21/Techniques/general/G17.html#tests – Devisal

Why does it say "the standard coefficients for sRGB" in step 3, when the previous step was going from sRGB to a linear RGB? I was under impression that linear RGB exists as to be "universal" among different chromaticity coordinates of RGB systems? The formula in step 2 you use is the one for sRGB, so why would in step 3 it matter which gamma-encoded RGB was used before transformation to linear? – Voyage

@Lazar Ljubenović the coefficients need to be applied to the linearized data, not gamma encoded data. And no, the coefficients are not universal, they vary per the color space. Remember that we humans do NOT see the visible spectrum evenly. Green makes up the majority of luminance, then red, and blue a very tiny (and sometimes negative) effect on perceived luminance. "RGB" is definitely not universal!! Different primaries require different coefficients. – Chantry

Thank your for an excellent answer. One slight quibble: your function YtoLstar(Y) takes a value in the range 0 to 1, and returns one in the range 0 to 100, which is a bit confusing. – Instrumentalist

Hi @ChrisDennis thank you — so, commonly, Y is a 0.0-1.0 range, and L* is commonly 0-100. Sometimes Y is normalized to 0-100, in which case it must be shifted to 0.0-1.0 before applying the exponents for the power curve. L* is almost always a 0-100 range, and the ab color values are often ±128. L* is based/derived from Munsell value, which is 0-10 ... So, as for confusing, wait till you dig deeper into colorimetry—"confusing" is par for the course. (!!) – Chantry

Small typo... seems if ( Y <= (216/24389) { is missing a ) – Voltage

Hi @OGSean You are correct!! That's a typo (I'm kinda blind)... and since it was pseudocode, it was not actually tested. Thank you!! – Chantry

I see you and Bruce Lindbloom agree on the constants for the L* conversion; that's a good thing, I've worked with Bruce and he's brilliant. Any idea of how that power of 1/3 came about? It's like no gamma I've ever heard of. – Jettiejettison

Hi @MarkRansom ... all of visual perception has some wiggle-bits, and lots of approximations—but for the rational constants in L*, I understand Bruce made a correction that the CIE later adopted. So yea, brilliant! The power of ⅓ is not a gamma such as for a display, it's the power curve exponent to fit the renotated Munsell Value parameter, which the CIE used for LAB and LUV in 1976. The corollary to a display gamma would be 3.0 if taken at face value, but there is an offset/scale as well (rec709 and sRGB do similar tricks) continued.... – Chantry

Hi @MarkRansom (cont) ...The effect of the offset is an "effective" exponent of about 0.425 (ish, or 1/2.35) but that depends on the adaptation state, and the reference peak luminance, amongst other things. So this is all a long winded way of saying that ⅓ with the offset and scale, in a specific reference viewing/adaptation environment, represents the human visual system's "eye gamma" looking at diffuse patches of surface colors of a low spatial frequency. ... or words to that effect... 😎 Thank you for reading! – Chantry

I was aware of how sRGB uses a power of 2.4 to approximate a power 2.2, so it doesn't surprise me that this was another case of that trick being used. I couldn't find a reference to justify it though, it's just a magic constant. When I tried to research the eye's non-linearity a few years ago I found a reference to a power of 1/2.4, which is within the margin of error I think to 1/2.35. – Jettiejettison

Hi @MarkRansom and in fact the "margin of variability" is greater than that, as the actual perception curve is dependent on spatial frequency, adaptation level vs peak, surround context, not to mention the changes from photopic to mesopic to scotopic vision... "...and a partridge in a pear tree..." for instance Stevens indicated ⅓ to ½ depending on spatial frequency. The point being, it is far from absolute, and very context sensitive. – Chantry

I converted this answer to TypeScript: gist.github.com/mnpenner/70ab4f0836bbee548c71947021f93607 – Bigotry

I created a 16 colors palette for programming, so I used the formula from the recommendation BT.601 to balance the Luma at 50% for every color. Should I have used the formula from the recommendation BT.709? Should I have corrected the gamma previously? I think I need to fix it after reading your post: github.com/gerardbm/atomic – Similar

@Similar First, "Luma" (Yʹ) is the gamma encoded signal, the linear signal is luminance Y. And yes you should use BT709, and yes you should linearize first before applying coefficients. but also, you might want to do your adjusting in a space like CIELUV or CIELAB od OKLAB for perceptual uniformity, luminance Y Is linear to light, but human perception is nonlinear. – Chantry

@Myndex, thanks! I've reviewed my work. What I was really doing is to use the model HSL to select a color every 60° of Hue, apply a 80-100% Saturation, I played manually with the Lightness to have 50% of Luma (Y'). How? I converted the HSL to RGB, so I applied the BT601 (wrong formula) directly over this RGB (wrong: not linearized). Over this RGB I calculated the relative luminance (wrong: using 0.03928 instead of 0.04045) to calculate the ratio contrast between bg and fg colours. What I don't know is how to use CIELAB instead of HSL. At the end what I want is a RGB color with a 50% Luma (Y'). – Similar

@Similar for your purposes you might prefer CIELUV which has satruation as part f the polar version. See: HSLuv.org ... with CIE LAB or LUV, the L* is perceptal lightness 0-100, so set it at 50 for your desired effect. – Chantry

@Myndex, thank you! I made a script to generate palettes of colors. It looks like it gives more weight to red, though. Now I have a base to work. I'm happy with this! i.imgur.com/eEBxobi.png – Similar

@Similar The coefficients, based on 1931 CIE XYZ, are intended to give you a neutral white or gray when all three primaries are at the same level, such as #eee... But there are other aspects of human vision like the HK effect, that causes saturated colors to seem more luminous than the calculated luminance would suggest. For better accuracy you need a much more complicated color model. Look into OKLab – Chantry

This article says middle grey for sRGB is at around 46%, not 50%. Is that accurate? – Sententious

Hi @DeepakSharma If you take a linear 18% signal, and apply the sRGB piecewise TRC, you get 46.13561295 ... If you want to have a conversation about "is 18% actually the middle gray", I could probably write a book entirely on that one subject. And also, 18% middle gray is not middle contrast, which is a different thing, and oddly, is about double the 18% gray. In linear, 36% to 37% is about middle contrast on a typical display. – Chantry

How do you calculate "colorChannel"? – Normanormal

Hi @Normanormal Step one above, assuming you have the three RGB channels separated in an array or object. If you mean, how do you take a 24bit integer that represents the three tuples, (i.e. step zero) there are a number of ways. I list three ways in this [older article on luminance ](myndex.com/WEB/LuminanceContrast#srgb-to-luminance). – Chantry

Answer 4

I have made comparison of the three algorithms in the accepted answer. I generated colors in cycle where only about every 400th color was used. Each color is represented by 2x2 pixels, colors are sorted from darkest to lightest (left to right, top to bottom).

1st picture - Luminance (relative)

0.2126 * R + 0.7152 * G + 0.0722 * B

2nd picture - http://www.w3.org/TR/AERT#color-contrast

0.299 * R + 0.587 * G + 0.114 * B

3rd picture - HSP Color Model

sqrt(0.299 * R^2 + 0.587 * G^2 + 0.114 * B^2)

4th picture - WCAG 2.0 SC 1.4.3 relative luminance and contrast ratio formula (see @Synchro's answer here)

Pattern can be sometimes spotted on 1st and 2nd picture depending on the number of colors in one row. I never spotted any pattern on picture from 3rd or 4th algorithm.

If i had to choose i would go with algorithm number 3 since its much easier to implement and its about 33% faster than the 4th.

Omentum

Your comparison image is incorrect because you did not provide the correct input to all of the functions. The first function requires linear RGB input; I can only reproduce the banding effect by providing nonlinear (i.e. gamma-corrected) RGB. Correcting this issue, you get no banding artifacts and the 1st function is the clear winner. – Durward

@Durward the ^2 and sqrt included in the third formula are a quicker way of approximating linear RGB from non-linear RGB instead of the ^2.2 and ^(1/2.2) that would be more correct. Using nonlinear inputs instead of linear ones is extremely common unfortunately. – Jettiejettison

Answer 5

Below is the only CORRECT algorithm for converting sRGB images, as used in browsers etc., to grayscale.

It is necessary to apply an inverse of the gamma function for the color space before calculating the inner product. Then you apply the gamma function to the reduced value. Failure to incorporate the gamma function can result in errors of up to 20%.

For typical computer stuff, the color space is sRGB. The right numbers for sRGB are approx. 0.21, 0.72, 0.07. Gamma for sRGB is a composite function that approximates exponentiation by 1/(2.2). Here is the whole thing in C++.

// sRGB luminance(Y) values
const double rY = 0.212655;
const double gY = 0.715158;
const double bY = 0.072187;

// Inverse of sRGB "gamma" function. (approx 2.2)
double inv_gam_sRGB(int ic) {
    double c = ic/255.0;
    if ( c <= 0.04045 )
        return c/12.92;
    else 
        return pow(((c+0.055)/(1.055)),2.4);
}

// sRGB "gamma" function (approx 2.2)
int gam_sRGB(double v) {
    if(v<=0.0031308)
      v *= 12.92;
    else 
      v = 1.055*pow(v,1.0/2.4)-0.055;
    return int(v*255+0.5); // This is correct in C++. Other languages may not
                           // require +0.5
}

// GRAY VALUE ("brightness")
int gray(int r, int g, int b) {
    return gam_sRGB(
            rY*inv_gam_sRGB(r) +
            gY*inv_gam_sRGB(g) +
            bY*inv_gam_sRGB(b)
    );
}

Scammony

Why did you use a composite function to approximate the exponent? Why not just do a direct calculation? Thanks – Tran

That is just the way sRGB is defined. I think the reason is that it avoids some numerical problems near zero. It would not make much difference if you just raised the numbers to the powers of 2.2 and 1/2.2. – Scammony

JMD - as part of work in a visual perception lab, I have done direct luminance measurements on CRT monitors and can confirm that there is a linear region of luminance at the bottom of the range of values. – Thrive

I know this is very old, but its still out there to be searched. I don't think it can be correct. Shouldn't gray(255,255,255) = gray(255,0,0)+gray(0,255,0)+gray(0,0,255)? It doesn't. – Platitudinize

@DCBillen: no, since the values are in non-linear gamma-corrected sRGB space, you can't just add them up. If you wanted to add them up, you should do so before calling gam_sRGB. – Mothball

Your gray function performs a gamma compression afterwards, but luminance itself is the uncompressed gray value, so if you want to compute the brightness then leave out the call togam_sRGB. If you just want to convert colors in order to display them black-and-white, then you should leave it in. – Achromat

Answer 6

Rather than getting lost amongst the random selection of formulae mentioned here, I suggest you go for the formula recommended by W3C standards.

Here's a straightforward but exact PHP implementation of the WCAG 2.0 SC 1.4.3 relative luminance and contrast ratio formulae. It produces values that are appropriate for evaluating the ratios required for WCAG compliance, as on this page, and as such is suitable and appropriate for any web app. This is trivial to port to other languages.

/**
 * Calculate relative luminance in sRGB colour space for use in WCAG 2.0 compliance
 * @link http://www.w3.org/TR/WCAG20/#relativeluminancedef
 * @param string $col A 3 or 6-digit hex colour string
 * @return float
 * @author Marcus Bointon <[email protected]>
 */
function relativeluminance($col) {
    //Remove any leading #
    $col = trim($col, '#');
    //Convert 3-digit to 6-digit
    if (strlen($col) == 3) {
        $col = $col[0] . $col[0] . $col[1] . $col[1] . $col[2] . $col[2];
    }
    //Convert hex to 0-1 scale
    $components = array(
        'r' => hexdec(substr($col, 0, 2)) / 255,
        'g' => hexdec(substr($col, 2, 2)) / 255,
        'b' => hexdec(substr($col, 4, 2)) / 255
    );
    //Correct for sRGB
    foreach($components as $c => $v) {
        if ($v <= 0.04045) {
            $components[$c] = $v / 12.92;
        } else {
            $components[$c] = pow((($v + 0.055) / 1.055), 2.4);
        }
    }
    //Calculate relative luminance using ITU-R BT. 709 coefficients
    return ($components['r'] * 0.2126) + ($components['g'] * 0.7152) + ($components['b'] * 0.0722);
}

/**
 * Calculate contrast ratio acording to WCAG 2.0 formula
 * Will return a value between 1 (no contrast) and 21 (max contrast)
 * @link http://www.w3.org/TR/WCAG20/#contrast-ratiodef
 * @param string $c1 A 3 or 6-digit hex colour string
 * @param string $c2 A 3 or 6-digit hex colour string
 * @return float
 * @author Marcus Bointon <[email protected]>
 */
function contrastratio($c1, $c2) {
    $y1 = relativeluminance($c1);
    $y2 = relativeluminance($c2);
    //Arrange so $y1 is lightest
    if ($y1 < $y2) {
        $y3 = $y1;
        $y1 = $y2;
        $y2 = $y3;
    }
    return ($y1 + 0.05) / ($y2 + 0.05);
}

Pinson

The W3C formula is incorrect on a number of levels. It is not taking human perception into account, they are using "simple" contrast using luminance which is linear and not at all perceptually uniform. Among other things, it appears they based it on some standards as old as 1988 (!!!) which are not relevant today (those standards were based on monochrome monitors such as green/black, and referred to the total contrast from on to off, not considering greyscale nor colors). – Chantry

That’s complete rubbish. Luma is specifically perceptual - that’s why it has different coefficients for red, green, and blue. Age has nothing to do with it - the excellent CIE Lab perceptual colour space dates from 1976. The W3C space isn’t as good, however it is a good practical approximation that is easy to calculate. If you have something constructive to offer, post that instead of empty criticism. – Pinson

@Syncro no, luma is a GAMMA ENCODED (Y´) part of some video encodings (such as NTSC's YIQ). Luminance, i.e. Y as in CIEXYZ is LINEAR, and not at all perceptual. the W3C are using linear luminance, and simple contrast, which does not properly define contrast in the mid range (it is way off). Writing an article on this right now, I'll post the link when complete. Yes, CIELAB is excellent, but W3C ARE NOT USING IT. The outdated doc I am referring to is ANSI-HFES-100-1988, and not appropriate for on-screen color contrasts. – Chantry

Just to add/update: we are currently researching replacement algorithms that better model perceptual contrast (discussion in Github Issue 695). However, as a separate issue FYI the threshold for sRGB is 0.04045, and not 0.03928 which was referenced from an obsolete early sRGB draft. The authoritative IEC std uses 0.04045 and a pull request is forthcoming to correct this error in the WCAG. (ref: IEC 61966-2-1:1999) This is in Github issue 360, though to mention, in 8bit there is no actual difference — near end of thread 360 I have charts of errors including 0.04045/0.03928 in 8bit. – Chantry

And to add to the thread, the replacement method for WCAG 3.0 is APCA, and can be seen at myndex.com/APCA/simple – Chantry

Answer 7

To add what all the others said:

All these equations work kinda well in practice, but if you need to be very precise you have to first convert the color to linear color space (apply inverse image-gamma), do the weight average of the primary colors and - if you want to display the color - take the luminance back into the monitor gamma.

The luminance difference between ingnoring gamma and doing proper gamma is up to 20% in the dark grays.

Evadne

Answer 8

Interestingly, this formulation for RGB=>HSV just uses v=MAX3(r,g,b). In other words, you can use the maximum of (r,g,b) as the V in HSV.

I checked and on page 575 of Hearn & Baker this is how they compute "Value" as well.

Antho

Just for the record the link is dead, archive version here - web.archive.org/web/20150906055359/http://… – Esma

HSV is not perceptually uniform (and it isn't even close). It is used only as a "convenient" way to adjust color, but it is not relevant to perception, and the V does not relate to the true value of L or Y (CIE Luminance). – Chantry

Does that mean #FF0000 is as bright as #FFFFFF? – Edinburgh

I believe it's more like lightness = (max(r, g, b) + min(r, g, b)) / 2 in HSL – Edinburgh

Answer 9

Consider this an addendum to Myndex's excellent answer. As he (and others) explain, the algorithms for calculating the relative luminance (and the perceptual lightness) of an RGB colour are designed to work with linear RGB values. You can't just apply them to raw sRGB values and hope to get the same results.

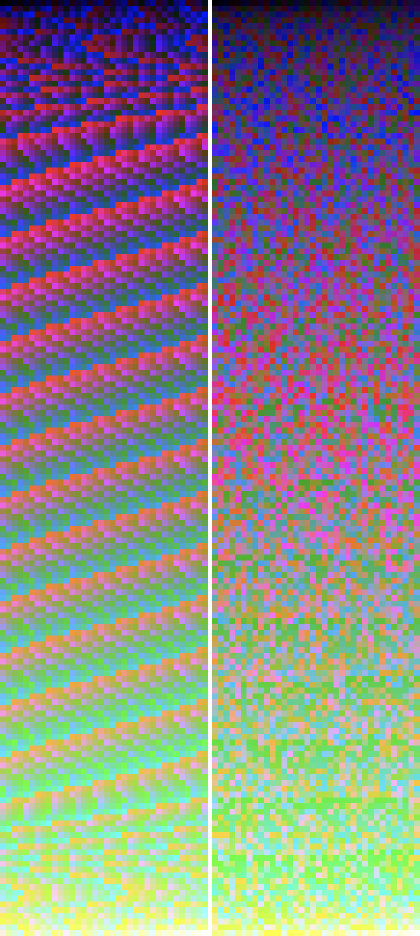
Well that all sounds great in theory, but I really needed to see the evidence for myself, so, inspired by Petr Hurtak's colour gradients, I went ahead and made my own. They illustrate the two most common algorithms (ITU-R Recommendation BT.601 and BT.709), and clearly demonstrate why you should do your calculations with linear values (not gamma-corrected ones).

Firstly, here are the results from the older ITU BT.601 algorithm. The one on the left uses raw sRGB values. The one on the right uses linear values.

ITU-R BT.601 colour luminance gradients

0.299 R + 0.587 G + 0.114 B

At this resolution, the left one actually looks surprisingly good! But if you look closely, you can see a few issues. At a higher resolution, unwanted artefacts are more obvious:

The linear one doesn't suffer from these, but there's quite a lot of noise there. Let's compare it to ITU-R Recommendation BT.709…

ITU-R BT.709 colour luminance gradients

0.2126 R + 0.7152 G + 0.0722 B

Oh boy. Clearly not intended to be used with raw sRGB values! And yet, that's exactly what most people do!

At high-res, you can really see how effective this algorithm is when using linear values. It doesn't have nearly as much noise as the earlier one. While none of these algorithms are perfect, this one is about as good as it gets.

Reis

Answer 10

I was solving a similar task today in javascript. I've settled on this getPerceivedLightness(rgb) function for a HEX RGB color. It deals with Helmholtz-Kohlrausch effect via Fairchild and Perrotta formula for luminance correction.

/**
 * Converts RGB color to CIE 1931 XYZ color space.
 * https://www.image-engineering.de/library/technotes/958-how-to-convert-between-srgb-and-ciexyz
 * @param  {string} hex
 * @return {number[]}
 */
export function rgbToXyz(hex) {
    const [r, g, b] = hexToRgb(hex).map(_ => _ / 255).map(sRGBtoLinearRGB)
    const X =  0.4124 * r + 0.3576 * g + 0.1805 * b
    const Y =  0.2126 * r + 0.7152 * g + 0.0722 * b
    const Z =  0.0193 * r + 0.1192 * g + 0.9505 * b
    // For some reason, X, Y and Z are multiplied by 100.
    return [X, Y, Z].map(_ => _ * 100)
}

/**
 * Undoes gamma-correction from an RGB-encoded color.
 * https://en.wikipedia.org/wiki/SRGB#Specification_of_the_transformation
 * https://mcmap.net/q/20665/-formula-to-determine-perceived-brightness-of-rgb-color
 * @param  {number}
 * @return {number}
 */
function sRGBtoLinearRGB(color) {
    // Send this function a decimal sRGB gamma encoded color value
    // between 0.0 and 1.0, and it returns a linearized value.
    if (color <= 0.04045) {
        return color / 12.92
    } else {
        return Math.pow((color + 0.055) / 1.055, 2.4)
    }
}

/**
 * Converts hex color to RGB.
 * https://mcmap.net/q/9259/-rgb-to-hex-and-hex-to-rgb
 * @param  {string} hex
 * @return {number[]} [rgb]
 */
function hexToRgb(hex) {
    const match = /^#?([a-f\d]{2})([a-f\d]{2})([a-f\d]{2})$/i.exec(hex)
    if (match) {
        match.shift()
        return match.map(_ => parseInt(_, 16))
    }
}

/**
 * Converts CIE 1931 XYZ colors to CIE L*a*b*.
 * The conversion formula comes from <http://www.easyrgb.com/en/math.php>.
 * https://github.com/cangoektas/xyz-to-lab/blob/master/src/index.js
 * @param   {number[]} color The CIE 1931 XYZ color to convert which refers to
 *                           the D65/2° standard illuminant.
 * @returns {number[]}       The color in the CIE L*a*b* color space.
 */
// X, Y, Z of a "D65" light source.
// "D65" is a standard 6500K Daylight light source.
// https://en.wikipedia.org/wiki/Illuminant_D65
const D65 = [95.047, 100, 108.883]
export function xyzToLab([x, y, z]) {
  [x, y, z] = [x, y, z].map((v, i) => {
    v = v / D65[i]
    return v > 0.008856 ? Math.pow(v, 1 / 3) : v * 7.787 + 16 / 116
  })
  const l = 116 * y - 16
  const a = 500 * (x - y)
  const b = 200 * (y - z)
  return [l, a, b]
}

/**
 * Converts Lab color space to Luminance-Chroma-Hue color space.
 * http://www.brucelindbloom.com/index.html?Eqn_Lab_to_LCH.html
 * @param  {number[]}
 * @return {number[]}
 */
export function labToLch([l, a, b]) {
    const c = Math.sqrt(a * a + b * b)
    const h = abToHue(a, b)
    return [l, c, h]
}

/**
 * Converts a and b of Lab color space to Hue of LCH color space.
 * https://mcmap.net/q/20773/-conversion-of-cielab-to-cielch-ab-not-yielding-correct-result
 * @param  {number} a
 * @param  {number} b
 * @return {number}
 */
function abToHue(a, b) {
    if (a >= 0 && b === 0) {
        return 0
    }
    if (a < 0 && b === 0) {
        return 180
    }
    if (a === 0 && b > 0) {
        return 90
    }
    if (a === 0 && b < 0) {
        return 270
    }
    let xBias
    if (a > 0 && b > 0) {
        xBias = 0
    } else if (a < 0) {
        xBias = 180
    } else if (a > 0 && b < 0) {
        xBias = 360
    }
    return radiansToDegrees(Math.atan(b / a)) + xBias
}

function radiansToDegrees(radians) {
    return radians * (180 / Math.PI)
}

function degreesToRadians(degrees) {
    return degrees * Math.PI / 180
}

/**
 * Saturated colors appear brighter to human eye.
 * That's called Helmholtz-Kohlrausch effect.
 * Fairchild and Pirrotta came up with a formula to
 * calculate a correction for that effect.
 * "Color Quality of Semiconductor and Conventional Light Sources":
 * https://books.google.ru/books?id=ptDJDQAAQBAJ&pg=PA45&lpg=PA45&dq=fairchild+pirrotta+correction&source=bl&ots=7gXR2MGJs7&sig=ACfU3U3uIHo0ZUdZB_Cz9F9NldKzBix0oQ&hl=ru&sa=X&ved=2ahUKEwi47LGivOvmAhUHEpoKHU_ICkIQ6AEwAXoECAkQAQ#v=onepage&q=fairchild%20pirrotta%20correction&f=false
 * @return {number}
 */
function getLightnessUsingFairchildPirrottaCorrection([l, c, h]) {
    const l_ = 2.5 - 0.025 * l
    const g = 0.116 * Math.abs(Math.sin(degreesToRadians((h - 90) / 2))) + 0.085
    return l + l_ * g * c
}

export function getPerceivedLightness(hex) {
    return getLightnessUsingFairchildPirrottaCorrection(labToLch(xyzToLab(rgbToXyz(hex))))
}

Shriek

Answer 11

Here's a bit of C code that should properly calculate perceived luminance.

// reverses the rgb gamma
#define inverseGamma(t) (((t) <= 0.0404482362771076) ? ((t)/12.92) : pow(((t) + 0.055)/1.055, 2.4))

//CIE L*a*b* f function (used to convert XYZ to L*a*b*)  http://en.wikipedia.org/wiki/Lab_color_space
#define LABF(t) ((t >= 8.85645167903563082e-3) ? powf(t,0.333333333333333) : (841.0/108.0)*(t) + (4.0/29.0))


float
rgbToCIEL(PIXEL p)
{
   float y;
   float r=p.r/255.0;
   float g=p.g/255.0;
   float b=p.b/255.0;

   r=inverseGamma(r);
   g=inverseGamma(g);
   b=inverseGamma(b);

   //Observer = 2°, Illuminant = D65 
   y = 0.2125862307855955516*r + 0.7151703037034108499*g + 0.07220049864333622685*b;

   // At this point we've done RGBtoXYZ now do XYZ to Lab

   // y /= WHITEPOINT_Y; The white point for y in D65 is 1.0

    y = LABF(y);

   /* This is the "normal conversion which produces values scaled to 100
    Lab.L = 116.0*y - 16.0;
   */
   return(1.16*y - 0.16); // return values for 0.0 >=L <=1.0
}

Ravage

Answer 12

As mentioned by @Nils Pipenbrinck:

All these equations work kinda well in practice, but if you need to be very precise you have to [do some extra gamma stuff]. The luminance difference between ignoring gamma and doing proper gamma is up to 20% in the dark grays.

Here's a fully self-contained JavaScript function that does the "extra" stuff to get that extra accuracy. It's based on Jive Dadson's C++ answer to this same question.

// Returns greyscale "brightness" (0-1) of the given 0-255 RGB values
// Based on this C++ implementation: https://mcmap.net/q/20665/-formula-to-determine-perceived-brightness-of-rgb-color
function rgbBrightness(r, g, b) {
  let v = 0;
  v += 0.212655 * ((r/255) <= 0.04045 ? (r/255)/12.92 : Math.pow(((r/255)+0.055)/1.055, 2.4));
  v += 0.715158 * ((g/255) <= 0.04045 ? (g/255)/12.92 : Math.pow(((g/255)+0.055)/1.055, 2.4));
  v += 0.072187 * ((b/255) <= 0.04045 ? (b/255)/12.92 : Math.pow(((b/255)+0.055)/1.055, 2.4));
  return v <= 0.0031308 ? v*12.92 : 1.055 * Math.pow(v,1.0/2.4) - 0.055;
}

See Myndex's answer for a more accurate calculation.

Neel

Answer 13

RGB Luminance value = 0.3 R + 0.59 G + 0.11 B

http://www.scantips.com/lumin.html

If you're looking for how close to white the color is you can use Euclidean Distance from (255, 255, 255)

I think RGB color space is perceptively non-uniform with respect to the L2 euclidian distance. Uniform spaces include CIE LAB and LUV.

Suazo

Answer 14

The inverse-gamma formula by Jive Dadson needs to have the half-adjust removed when implemented in Javascript, i.e. the return from function gam_sRGB needs to be return int(v*255); not return int(v*255+.5); Half-adjust rounds up, and this can cause a value one too high on a R=G=B i.e. grey colour triad. Greyscale conversion on a R=G=B triad should produce a value equal to R; it's one proof that the formula is valid. See Nine Shades of Greyscale for the formula in action (without the half-adjust).

Clownery

I did the experiment. In C++ it needs the +0.5, so I put it back in. I added a comment about translating to other languages. – Scammony

Answer 15

I wonder how those rgb coefficients were determined. I did an experiment myself and I ended up with the following:

Y = 0.267 R + 0.642 G + 0.091 B

Close but but obviously different than the long established ITU coefficients. I wonder if those coefficients could be different for each and every observer, because we all may have a different amount of cones and rods on the retina in our eyes, and especially the ratio between the different types of cones may differ.

For reference:

ITU BT.709:

Y = 0.2126 R + 0.7152 G + 0.0722 B

ITU BT.601:

Y = 0.299 R + 0.587 G + 0.114 B

I did the test by quickly moving a small gray bar on a bright red, bright green and bright blue background, and adjusting the gray until it blended in just as much as possible. I also repeated that test with other shades. I repeated the test on different displays, even one with a fixed gamma factor of 3.0, but it all looks the same to me. More over, the ITU coefficients literally are wrong for my eyes.

And yes, I presumably have a normal color vision.

Cabbala

In your experiments did you linearize to remove the gamma component first? If you didn't that could explain your results. BUT ALSO, the coefficients are related to the CIE 1931 experiments and those are an average of 17 observers, so yes there is individual variance in results. – Chantry

And to add: Also, the 1931 CIE values are based on a 2° observer, and in addition there are known errors in the blue region. The 10° observer values are significantly different as the S cones are not in the foveal central vision. In both cases, effort was made to avoid rod intrusion, keeping the luminance levels in the photopic area. If measurements are made in the mesopic region, rod intrusion will also skew results. – Chantry

Answer 16

The answer from Myindex coded in Java:

public static double calculateRelativeLuminance(Color color)
{
    double red = color.getRed() / 255.0;
    double green = color.getGreen() / 255.0;
    double blue = color.getBlue() / 255.0;

    double r = (red <= 0.04045) ? red / 12.92 : Math.pow((red + 0.055) / 1.055, 2.4);
    double g = (green <= 0.04045) ? green / 12.92 : Math.pow((green + 0.055) / 1.055, 2.4);
    double b = (blue <= 0.04045) ? blue / 12.92 : Math.pow((blue + 0.055) / 1.055, 2.4);

    return 0.2126 * r + 0.7152 * g + 0.0722 * b;
}

I used it to calculate the contrast ratio of the background color and determine if the text color would be bright or not. Full example:

public static boolean isBright(Color backgroundColor)
{
    double backgroundLuminance = calculateRelativeLuminance(backgroundColor);
    double whiteContrastRatio = calculateContrastRatio(backgroundLuminance, 1.0);
    double blackContrastRatio = calculateContrastRatio(backgroundLuminance, 0.0);
    return whiteContrastRatio > blackContrastRatio;
}

public static double calculateRelativeLuminance(Color color)
{
    double red = color.getRed() / 255.0;
    double green = color.getGreen() / 255.0;
    double blue = color.getBlue() / 255.0;

    double r = (red <= 0.04045) ? red / 12.92 : Math.pow((red + 0.055) / 1.055, 2.4);
    double g = (green <= 0.04045) ? green / 12.92 : Math.pow((green + 0.055) / 1.055, 2.4);
    double b = (blue <= 0.04045) ? blue / 12.92 : Math.pow((blue + 0.055) / 1.055, 2.4);

    return 0.2126 * r + 0.7152 * g + 0.0722 * b;
}

public static double calculateContrastRatio(double backgroundLuminance, double textLuminance)
{
    var brightest = Math.max(backgroundLuminance, textLuminance);
    var darkest = Math.min(backgroundLuminance, textLuminance);
    return (brightest + 0.05) / (darkest + 0.05);
}

Jargon

Answer 17

The HSV colorspace should do the trick, see the wikipedia article depending on the language you're working in you may get a library conversion .

H is hue which is a numerical value for the color (i.e. red, green...)

S is the saturation of the color, i.e. how 'intense' it is

V is the 'brightness' of the color.

Bohs

Problem with the HSV color space is that you can have the same saturation and value, but different hue's, for blue and yellow. Yellow is much brighter than blue. Same goes for HSL. – Untwist

hsv gives you the "brightness" of a color in a technical sense. in a perceptual brightness hsv really fails – Berthold

HSV and HSL are not perceptually accurate (and it's not even close). They are useful for "controls" for adjusting relative color, but not for accurate prediction of perceptual lightness. Use L* from CIELAB for perceptual lightness. – Chantry

Answer 18

A single line:

brightness = 0.2*r + 0.7*g + 0.1*b

When r,g,b values are between 0 to 255, then the brightness scale is also between 0 (black) to 255 (white).

It can be fine-tuned of course, but I've found it to be sufficient for most use case.

Anny

Answer 19

The 'V' of HSV is probably what you're looking for. MATLAB has an rgb2hsv function and the previously cited wikipedia article is full of pseudocode. If an RGB2HSV conversion is not feasible, a less accurate model would be the grayscale version of the image.

Fusion

Answer 20

To determine the brightness of a color with R, I convert the RGB system color in HSV system color.

In my script, I use the HEX system code before for other reason, but you can start also with RGB system code with rgb2hsv {grDevices}. The documentation is here.

Here is this part of my code:

 sample <- c("#010101", "#303030", "#A6A4A4", "#020202", "#010100")
 hsvc <-rgb2hsv(col2rgb(sample)) # convert HEX to HSV
 value <- as.data.frame(hsvc) # create data.frame
 value <- value[3,] # extract the information of brightness
 order(value) # ordrer the color by brightness

Ehling

Answer 21

For clarity, the formulas that use a square root need to be

sqrt(coefficient * (colour_value^2))

not

sqrt((coefficient * colour_value))^2

The proof of this lies in the conversion of a R=G=B triad to greyscale R. That will only be true if you square the colour value, not the colour value times coefficient. See Nine Shades of Greyscale

Clownery

there are parenthesis mistmatches – Shipley

unless the coefficient you use is the square root of the correct coefficient. – Fusee

Answer 22

Please define brightness. If you're looking for how close to white the color is you can use Euclidean Distance from (255, 255, 255)

Glint

No, you can't use euclidian distance between sRGB values, sRGB is not a perceptually uniform Cartesian/vector space. If you want to use Euclidian distance as a measure of color difference, you need to at least convert to CIELAB, or better yet, use a CAM like CIECAM02. – Chantry