I am currently trying to detect the edge of a prism shape materials and find the angle of that shape.
I have an original image like this:
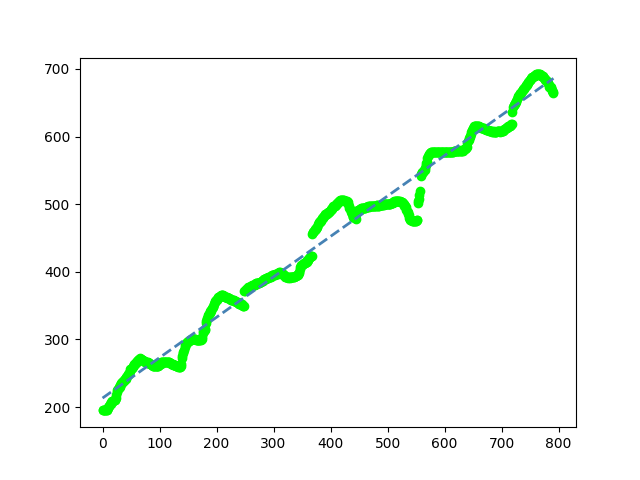
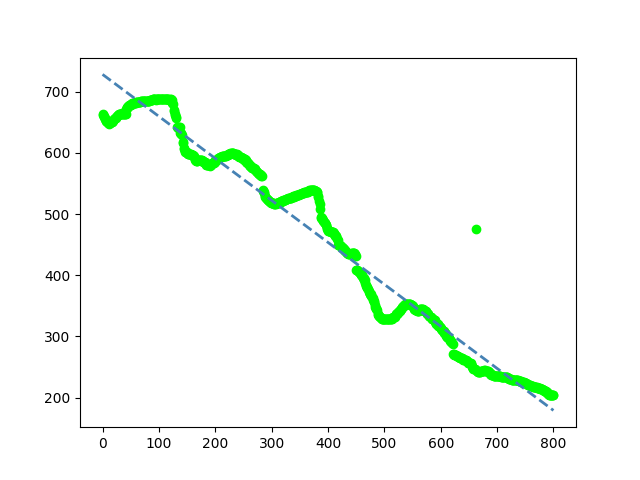
I wrote a Python program that detects the edge between burgundy background and grey materials (the code is given below) and it detects the edges like this:
But I don't know how to find angle from the detected edge. Any ideas?
import glob
import cv2
import numpy as np
import ctypes
import math
def get_screen_resolution():
user32 = ctypes.windll.user32
return user32.GetSystemMetrics(0), user32.GetSystemMetrics(1)
def process_photos():
# Get the list of image files in the directory
image_files = glob.glob("LEF_*.jpg")
# Process each image file
for image_file in image_files:
process_image(image_file)
def process_image(image_file):
# Load the image
image = cv2.imread(image_file)
# Convert the image to grayscale
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
# Perform color-based segmentation to extract the burgundy regions
lower_burgundy = np.array([0, 0, 100]) # Adjust the lower threshold for burgundy color
upper_burgundy = np.array([100, 100, 255]) # Adjust the upper threshold for burgundy color
mask = cv2.inRange(image, lower_burgundy, upper_burgundy)
# Apply a Gaussian blur to the mask to reduce noise
blurred_mask = cv2.GaussianBlur(mask, (5, 5), 0)
# Perform Canny edge detection on the grayscale image
edges_gray = cv2.Canny(gray, 50, 150)
# Combine the edges with the burgundy regions using bitwise AND
combined_edges = cv2.bitwise_and(edges_gray, blurred_mask)
# Dilate the edges to enhance connectivity
dilated = cv2.dilate(combined_edges, None, iterations=2)
# Find contours of the edges
contours, _ = cv2.findContours(dilated.copy(), cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
# Approximate the contours to straight lines
lines = cv2.HoughLinesP(dilated, rho=1, theta=np.pi/180, threshold=100, minLineLength=100, maxLineGap=10)
# Draw the lines on the original image
if lines is not None:
# Compute the mean line from the detected line segments
mean_x1, mean_y1, mean_x2, mean_y2 = np.mean(lines[:, 0, :], axis=0, dtype=np.int32)
# Draw the mean line
cv2.line(image, (mean_x1, mean_y1), (mean_x2, mean_y2), (0, 255, 0), 2)
# Compute the angle of the mean line
angle = math.atan2(mean_y2 - mean_y1, mean_x2 - mean_x1) * 180 / np.pi
print("Angle:", angle)
# Draw the contours on the original image
cv2.drawContours(image, contours, -1, (0, 255, 0), 2)
# Resize the image to fit the screen resolution
screen_width, screen_height = get_screen_resolution()
image = cv2.resize(image, (screen_width, screen_height))
# Display the processed image
cv2.imshow("Processed Image", image)
cv2.waitKey(0)
cv2.destroyAllWindows()
process_photos()





(0,y0) - (x1,y1) - (image width,y2), degree of freedom is only 4. – Bathesda