how to apply gradients manually in pytorch

Question

Starting to learn pytorch and was trying to do something very simple, trying to move a randomly initialized vector of size 5 to a target vector of value [1,2,3,4,5].

But my distance is not decreasing!! And my vector x just goes crazy. No idea what I am missing.

import torch
import numpy as np
from torch.autograd import Variable

# regress a vector to the goal vector [1,2,3,4,5]

dtype = torch.cuda.FloatTensor # Uncomment this to run on GPU

x = Variable(torch.rand(5).type(dtype), requires_grad=True)
target = Variable(torch.FloatTensor([1,2,3,4,5]).type(dtype), 
requires_grad=False)
distance = torch.mean(torch.pow((x - target), 2))

for i in range(100):
  distance.backward(retain_graph=True)
  x_grad = x.grad
  x.data.sub_(x_grad.data * 0.01)

Burchette

Does my answer solve your question or not? Why don't you give any feedback? – Juristic

Answer 1

There are two errors in your code that prevents you from getting the desired results.

The first error is that you should put the distance calculation in the loop. Because the distance is the loss in this case. So we have to monitor its change in each iteration.

The second error is that you should manually zero out the x.grad because pytorch won't zero out the grad in variable by default.

The following is an example code which works as expected:

import torch
import numpy as np
from torch.autograd import Variable
import matplotlib.pyplot as plt

# regress a vector to the goal vector [1,2,3,4,5]

dtype = torch.cuda.FloatTensor # Uncomment this to run on GPU

x = Variable(torch.rand(5).type(dtype), requires_grad=True)
target = Variable(torch.FloatTensor([1,2,3,4,5]).type(dtype), 
requires_grad=False)

lr = 0.01 # the learning rate

d = []
for i in range(1000):
  distance = torch.mean(torch.pow((x - target), 2))
  d.append(distance.data)
  distance.backward(retain_graph=True)

  x.data.sub_(lr * x.grad.data)
  x.grad.data.zero_()

print(x.data)

fig, ax = plt.subplots()
ax.plot(d)
ax.set_xlabel("iteration")
ax.set_ylabel("distance")
plt.show()

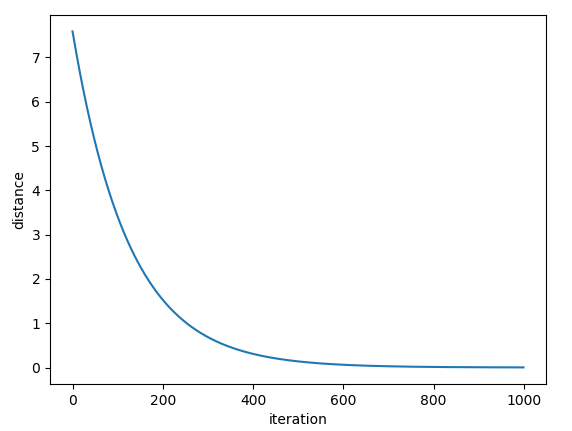
The following is the graph of distance w.r.t iteration

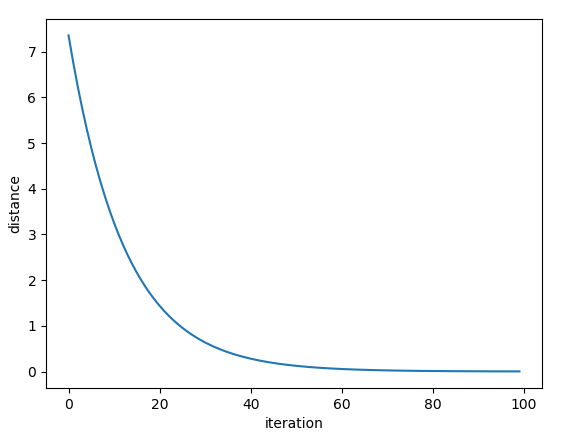
We can see that the model converges at about 600 iterations. If we set the learning rate to be higher (e.g, lr=0.1), the model will converge much faster (it takes about 60 iterations, see image below)

Now, x becomes something like the following

0.9878 1.9749 2.9624 3.9429 4.9292

which is pretty close to your target of [1, 2, 3, 4, 5].

Juristic