Fading Colors in a Graph

Question

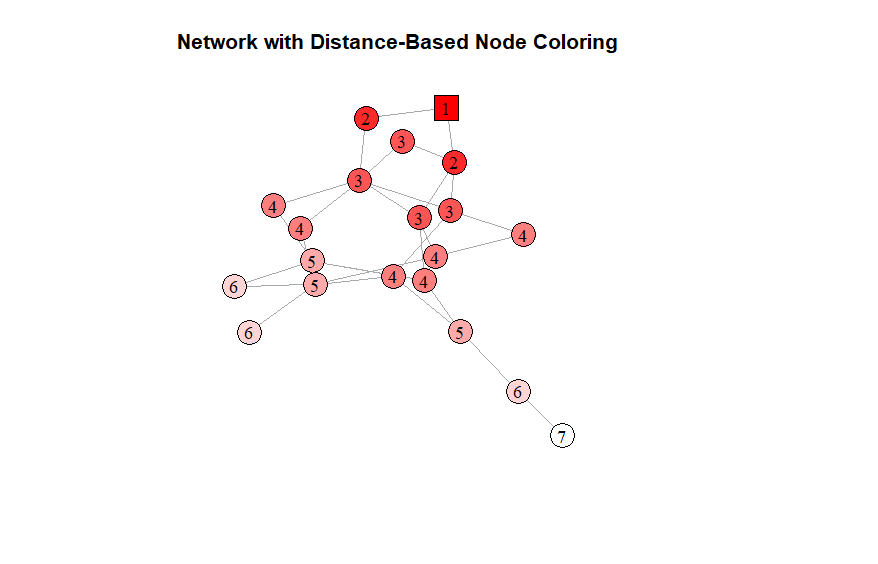
I have a random graph in R in which one random node is colored red (square) - and all other nodes are colored lighter shades of red relative to their distance from the original node (i.e. based on "degree"):

 library(igraph)
library(colorRamps)

set.seed(123)

n_nodes <- 20  
n_edges <- 30 
g <- erdos.renyi.game(n_nodes, n_edges, type = "gnm")

random_red_node <- sample(1:n_nodes, 1)

distances <- distances(g, v = random_red_node, to = V(g))
max_distance <- max(distances)

color_palette <- colorRampPalette(c("red", "white"))(max_distance + 1)

node_colors <- color_palette[distances + 1]
node_colors[random_red_node] <- "red"

node_shapes <- rep("circle", n_nodes)
node_shapes[random_red_node] <- "square"

node_labels <- distances + 1

par(mar = c(5, 4, 4, 8), xpd = TRUE)

plot(g,
     vertex.color = node_colors,
     vertex.size = 15,
     vertex.label = node_labels,
     vertex.label.color = "black",
     vertex.shape = node_shapes,
     vertex.frame.color = "black",
     edge.arrow.size = 0.5,
     main = "Network with Distance-Based Node Coloring")

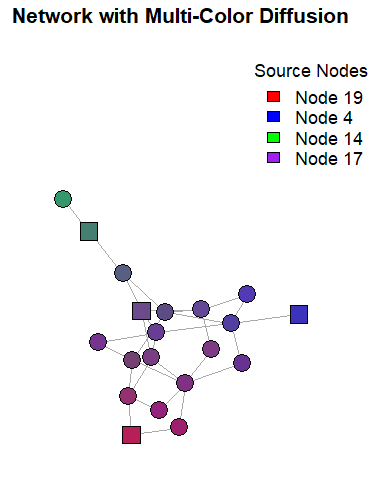
I am trying to change this so that now I can have multiple square nodes of different colors, and the same fading is applied:

The idea is to mimic diffusion of colors such that they create natural boundaries.

Thank you.

Here is a question that might help: How to tell if a point has been colored twice in R?

---

edit: My approach - this only works for a few nodes and will not work for multiple source nodes of the same color (e.g. multiple reds)

First, I use a function to define the color gradients:

library(igraph)
library(colorRamps)

set.seed(123)

blend_colors <- function(colors, weights) {
    if (length(colors) != length(weights)) stop("")
    
    rgb_colors <- col2rgb(colors)
    blended <- rowSums(rgb_colors %*% diag(weights)) / sum(weights)
    rgb(blended[1], blended[2], blended[3], maxColorValue = 255)
}

I then generate a network for the problem:

n_nodes <- 20
n_edges <- 30
g <- erdos.renyi.game(n_nodes, n_edges, type = "gnm")

n_colored_nodes <- 4
colored_nodes <- sample(1:n_nodes, n_colored_nodes)
node_colors <- c("red", "blue", "green", "purple")[1:n_colored_nodes]

The fading is a function of distance, I tried to capture this idea:

distances_list <- lapply(colored_nodes, function(node) {
  distances(g, v = node, to = V(g))
})
max_distance <- max(unlist(distances_list))
normalized_distances <- lapply(distances_list, function(d) {
  1 - (d / max_distance)
})

Here is how I call this :

blended_colors <- sapply(1:n_nodes, function(i) {
  weights <- sapply(normalized_distances, function(d) d[i])
  blend_colors(node_colors, weights)
})

node_shapes <- rep("circle", n_nodes)
node_shapes[colored_nodes] <- "square"

par(mar = c(5, 4, 4, 8), xpd = TRUE)

plot(g,
     vertex.color = blended_colors,
     vertex.size = 15,
     vertex.label = NA,
     vertex.shape = node_shapes,
     vertex.frame.color = "black",
     edge.arrow.size = 0.5,
     main = "Network with Multi-Color Diffusion")

legend("topright", inset = c(-0.2, 0), 
       legend = paste("Node", colored_nodes), 
       fill = node_colors, 
       title = "Source Nodes", 
       bty = "n")

Lennox

The question currently reads like a code-writing request. It is more likely to draw helpful feedback after providing the code already tried (e. g. by starting with the answers to the related question) and describing how (if) it failed to work as desired. – Ceratoid

@ I_O: Sure, I can show what I tried already ... I am not confident in the approach. But OK, sure, I will post – Lennox

Answer 1

Not sure what's the big picture here, but I changed the logic a bit:

• source node colors are fixed and not updated
• distance calculation through breath-first search starting from source (color) nodes, other source nodes are excluded from each search; this means that source nodes that are only accessible through other source nodes do not contribute anymore, for example in a network 1 - Red - Blue - 2, 1 becomes Red and not 2/3 Red + 1/3 Blue; and 2 becomes Blue
• color blending with colorjam::blend_colors(), it blends multiple colors and uses alpha values for weights; and as jamba comes as a dependency anyway, jamba::alpha2col() for setting alpha values; colorjam is currently only available from Github, remotes::install_github("jmw86069/colorjam")
• inverse distance weights for each non-source node sum up to 1, so there should be no issues with different number of source nodes or with multiple source nodes of the same color; this also plays nice with jamba::alpha2col() & colorjam::blend_colors() defaults.

# remotes::install_github("jmw86069/colorjam")
library(igraph, warn.conflicts = FALSE)

blend_colors <- function(colors, weights) {
  colors  <- na.omit(colors)
  weights <- na.omit(weights)
  if (length(colors) != length(weights)) stop("legth mismatch")
  # weights should add to 1, but let's leave some floating point margin
  if (sum(weights) > 1.1) stop("weights sum > 1.1")
  
  jamba::alpha2col(colors, weights) |> 
    colorjam::blend_colors()
}

color_g <- function(g, node_colors = c("red", "green", "blue")){
  # named vertices to get named lists and named matrices
  V(g)$name <- V(g)
  # for more convenient source / non-source vertex subsets
  V(g)$src <- FALSE
  
  # mark a set of length(node_colors) as src nodes, assign input colors
  # V(g)[sample(name, length(node_colors))]$src <- TRUE
  V(g)[sample(V(g), length(node_colors))]$src <- TRUE
  V(g)[ src]$color <- sample(node_colors)
  V(g)[!src]$color <- "white"
  
  V(g)[ src]$shape <- "square"
  V(g)[!src]$shape <- "circle"
  
  # breath-first search from each src node, restricted to non-src nodes + itself to
  # find distances without going through other src nodes; -1 == unreachable (not in a restricted list) 
  dist_from_src <- 
    lapply(
      V(g)[src], 
      \(v_src) bfs(g, v_src, unreachable = FALSE, restricted = c(v_src, V(g)[!src]), dist = TRUE)$dist
    ) |> 
    do.call(what = rbind)
  # with 10 nodes, 15 edges, 3 src/color nodes (3:R, 5:G, 9:B):
  #   1 2  3 4  5 6 7 8  9 10
  # 3 2 2  0 1 -1 2 1 1 -1 -1
  # 5 3 2 -1 3  0 1 1 2 -1  1
  # 9 1 2 -1 1 -1 4 3 3  0  1  

  # exclude source node columns, transpose; 
  # with actual colors in column names we can later conveniently 
  # extract named weight vectors
  color_dist <- 
    dist_from_src[, -V(g)[src]] |> 
    `rownames<-`(V(g)[src]$color) |> 
    t()
  color_dist[color_dist < 1] <- NA
  
  inv_dist_color_weights <- (1/color_dist) / rowSums(1/color_dist, na.rm = TRUE)
  # with 10 nodes, 15 edges, 3 colors:
  #     red green blue <- V: 3 5 9
  # 1  0.27  0.18 0.55
  # 2  0.33  0.33 0.33
  # 4  0.43  0.14 0.43
  # 6  0.29  0.57 0.14
  # 7  0.43  0.43 0.14
  # 8  0.55  0.27 0.18
  # 10   NA  0.50 0.50  

  # each row in inv_dist_color_weights matrix is a set of weights, 
  # colors in column names, NA colors did not contribute; 
  # extract named vectors, omit NAs, pass names(colors) and weights 
  # to blend_colors(); update non-source vertices
  V(g)[!src]$color <- 
    apply(inv_dist_color_weights, 1, c, simplify = F) |> 
    lapply(na.omit) |> 
    sapply(\(cw) blend_colors(names(cw), cw))
  
  g
}

set.seed(123)
n_nodes <- 20
n_edges <- 30

g <- sample_gnm(n_nodes, n_edges)
g_c <- color_g(g, c("red", "blue", "green", "red", "blue"))
withr::with_par(
  list(mar = c(0, 0, 0, 0)),
  plot(g_c)
)

---

Few others:

g_2 <- color_g(make_tree(n = 33, mode = "undirected"), colorjam::rainbowJam(5, preset = "ryb"))
g_3 <- color_g(make_lattice(dimvector = c(5,5)), c("red", "red", "gold"))
withr::with_par(
  list(mfrow = c(1,2), mar = c(0, 0, 0, 0)),
  {
    plot(g_2)
    plot(g_3)
  }
)

^{Created on 2024-09-13 with reprex v2.1.1}

Sidestroke

thank you so much for your answer! Again, I am trying to think how to simulate diffusion. Imagine a horizontal swimming pool. From one side I dump red paint and the other side I dump green paint... the colors would be darker at the point where they entered... and become lighter and lighter until they collide. This is what I was trying to do – Lennox