I sometimes find it hard to use Isabelle because I cannot have a "print command" like in normal programming.
For example, I want to see what ?thesis. The concrete semantics book says:
The unknown ?thesis is implicitly matched against any goal stated by lemma or show. Here is a typical example:
My silly sample FOL proof is:
lemma
assumes "(∃ x. ∀ y. x ≤ y)"
shows "(∀x. ∃ y. y ≤ x)"
proof (rule allI)
show ?thesis
but I get the error:
proof (state)
goal (1 subgoal):
1. ⋀x. ∃y. y ≤ x
Failed to refine any pending goal
Local statement fails to refine any pending goal
Failed attempt to solve goal by exported rule:
∀x. ∃y. y ≤ x
but I do know why.
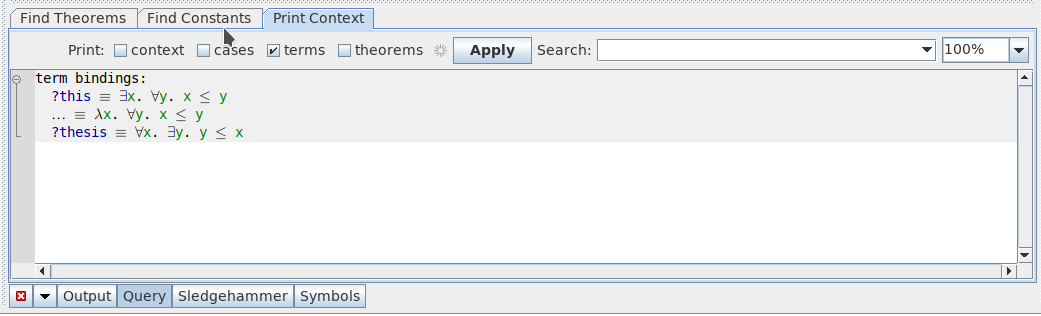
I expected
?thesis === ⋀x. ∃y. y ≤ x
since my proof state is:
proof (state)
goal (1 subgoal):
1. ⋀x. ∃y. y ≤ x
Why can't I print ?thesis?
It's really annoying to have to write the statement I'm trying to proof if it's obvious. Perhaps it's meant to be explicit but in the examples in chapter 5 they get away with using ?thesis in:
lemma fixes a b :: int assumes "b dvd (a+b)" shows "b dvd a" proof −
have "∃k′. a = b∗k′" if asm: "a+b = b∗k" for k proof
show "a = b∗(k − 1)" using asm by(simp add: algebra_simps) qed
then show ?thesis using assms by(auto simp add: dvd_def ) qed
but whenever I try to use ?thesis I always fail.
Why is it?
Note that this does work:
lemma
assumes "(∃ x. ∀ y. x ≤ y)"
shows "(∀x. ∃ y. y ≤ x)"
proof (rule allI)
show "⋀x. ∃y. y ≤ x" proof -
but I thought ?thesis was there to avoid this.
Also, thm ?thesis didn't work either.
Another example is when I use:
let ?ys = take k1 xs
but I can't print ?ys value.
TODO:
why doesn't:
lemma "length(tl xs) = length xs - 1"
thm (cases xs)
show anything? (same if your replaces cases with induction).