Can anyone explain the concept of free variables in Prolog. Is it similar to anonymous variables ? Or is there a difference. Also could be great if an example is given to explain.
Free Variable in Prolog
Asked Answered
tl;dr:
free is a notion to distinguish universally bound (free in clause notation) from existentially bound variables in setof/3, bagof/3, etc. - some people use free to mean "currently not instantiated" and some use it to denote an output argument that's meant to be instantiated by the predicate but that's not how the standard uses it.
long version: I will quote the Prolog standard on the definition:
7.1.1.4 Free variables set of a term The free variables set, FVt of a term T with respect to a term v is a set of variables defined as the set difference of the variable set (7.1.1.1) of T and BV where BV is a set of variables defined as the union of the variable set of v and the existential variables set (7.1.1.3) of T.
where they explicitly note:
The concept of a free variables set is required when defining bagof/3 (8.10.2) and setof/3 (8.10.3).
Perhaps as a background: in logic, a free variable is one that is not bound by a quantifier (e.g. x is bound and y is free in ∀x p(x,y) ). A (pure) prolog clause head(X) :- goal1(X), goal2(X). can be read as the logical formula ∀X goal1(X) ∧ goal2(X) → head(X). In practice, as long as we use fresh variables whenever we try to unify a goal with a clause, we can just disregard the universal quantifiers. So for our purposes we can treat X in the clause above as free.
This is all and well until meta-predicates come in: say we are interested in the set of first elements in a list of tuples:
?- setof(X, member(X-Y, [1-2, 2-2, 1-3]), Xs).
Y = 2,
Xs = [1, 2] ;
Y = 3,
Xs = [1].
But we get two solutions: the ones where Y=2 and those where Y=3. What I'd actually want to say is: there exists some Y such that X-Y is a member of the list. The Prolog notation for this pattern is to write Var^Term:
?- setof(X, Y^member(X-Y, [1-2, 2-2, 1-3]), Xs).
Xs = [1, 2].
In the first example, both X and Y are free, in the second example X is free and Y is bound.
If we write this as a formula we get setof(X, ∃Y member(X-Y, [1-2, 2-3, 1-3]), Xs) which is not a first order formula anymore (there is an equivalent first order one but this is where the name meta predicate comes in). Now the problem is that the Var^Term notation is purely syntactical - internally there is only one type of variable. But when we describe the behaviour of setof and friends we need to distinguish between free and existentially bound variables. So unless you are using metapredicates, all of your variables can be considered as free (1).
The Learning Prolog link provided by @Reema Q Khan is a bit fuzzy in its use of free. Just looking at the syntax, X is free in X=5, X is 2 + 3. But when we run this query, as soon as we get to the second goal, X has been instantiated to 5 so we are actually running the query 5 is 2 + 3 (2). What is meant in that context is that we expect is/3 to unify its first argument (often called "output" argument). To make sure this always succeeds we would pass a variable here (even though it's perfectly fine not to do it). The text tries to describe this expectation as "free variable" (3).
(1) ok, formally, anything that looks like Var^Term considers Var existentially bound but without meta-predicates this doesn't matter.
(2) I believe there is a clash in notation that some texts use "X is bound to 5" here, which might increase the confusion.
(3) What the should say is that they expect that the argument has not been instantiated yet but even that does not capture the semantics correctly - Paulo Moura already gave the initial ground example 5 is 3 + 2.
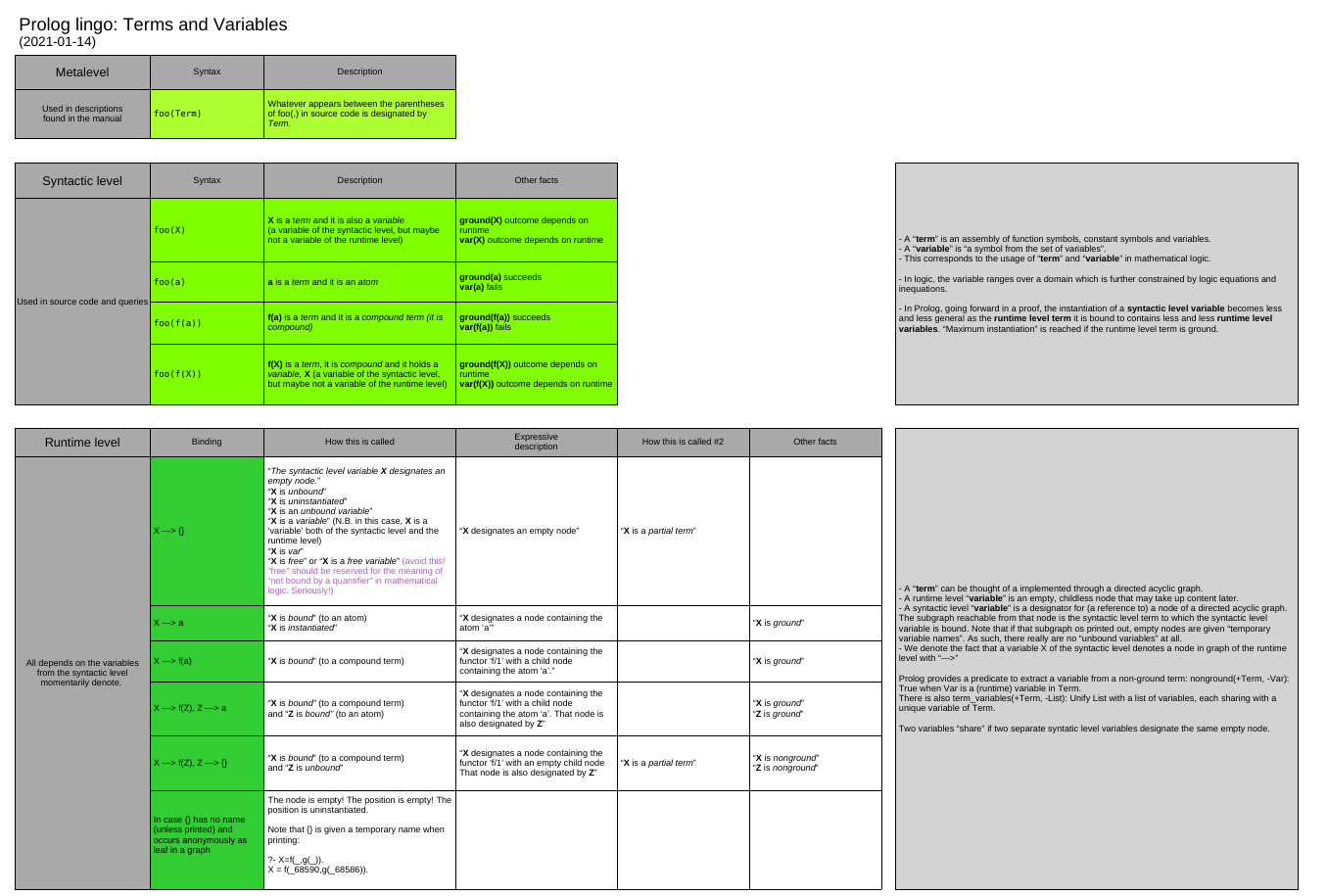
Maybe this can help. (If I have prepared it, I might as well post it! Still hard to read, needs simplification.)
In fact, you need to distinguish whether you talk about the syntax of the program or whether you talk about the runtime state of the program.
The word "variable" takes on slightly different meanings in both cases. In common usage, one does not make a distinction, and the understanding this fluent usage provides is good enough. But for beginners, this may be a hurdle.
In logic, the word "variable" has the meaning of "a symbol selected from the set of variable symbols", and it stands for the possibly infinite set of terms it may take on while fulfilling any constraints given by the logical formulae it participates in. This is not the "variable" used in reasoning about an actual programs.
Can you give an example like if X is written in such a way then it is a free variable, and if X is written in such a way then it is considered a anonymous variable? –
Philps
@ReemaQKhan These two words are not antonyms. A "free variable" is a variable that is not bound by a quantifier (in a logic formula) or a Lambda (in a lambda expression). Using it to signify that a variable is currently unbound at runtime is ... "not even wrong". The "anonymous variable" is just a notational phenomenon of Prolog code: wherever it appears in code, it shall be considered a fresh variable. This means it is always unbound, at least at first. It may become bound as in
_ = 2 but then you will never be able to read it as you cannot name it "the the right" of the =/2. –
Betthezel I really need to add more explanation to this Excel sheet. Not happy, –
Betthezel
Free Variable:
"is" is a build-in arithmetic evaluator in Prolog. "X is E" requires X to be free variable and E to be arithmetic expression that is possible to evaluate. E can contain variables but these variables has to be bound to numbers, e.g., "X=5, Y is 2*X" is correct Prolog goal.
More Explanation:
http://kti.ms.mff.cuni.cz/~bartak/prolog.old/learning/LearningProlog11.html
Anonymous Variable:
The name of every anonymous variable is _ .
More Explanation:
"X is E" requires X to be free variable". No, it doesn't. E.g.
4 is 4 is a perfectly valid goal. –
Raychel Try reading it as a whole. It is written in the context where X is a free variable. –
Philps
If you know C then you can compare a Prolog variable with a C variable that contains a pointer. As long as that pointer is null, the variable is free. Once the pointer is set, the variable is not free anymore.
This becomes interesting when trying to match two complex data structures with pointers in them. Basically, when walking the two structures in parallel, if a pointer is null on either side of the comparison, then it is like a wildcard.
Prolog goes further. When one side is null while the other one is not null then the null side gets the value of the other side and it is a match. As a result the "free" variable is not free anymore.
This "unification" process becomes even more interesting when trying to match a pattern with multiple other patterns, the one after the others
In Prolog, this involves yet another unusual concept named "backtracking". It's like walking backward in a labyrithm when encountering a dead end.
© 2022 - 2024 — McMap. All rights reserved.
bagof/3arguments), which is the meaning of "free" in first-order logic, or "free variables" as sloppy usage for "unbound (Prolog) variables" i.e. "variable names currently designating an empty cell in memory - aka. an empty term - as opposed to currently designating an actual non-empty term". Sadly, the latter usage is encountered from time to time. 😅 – Betthezel