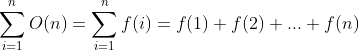What does this passage from CLRS mean?

Question

I came across this passage on page 47 of Introduction to Algorithms by Cormen et al.:

The number of anonymous functions in an expression is understood to be equal to the number of times the asymptotic notation appearrs. For example in the expression:

Σ (i=1 to n) O(i)

there is only a single anonymous function (a function of i). This expression is not the same as O(1) + O(2) + ... + O(n), which doesn't really have a clean interpretation.

What does this mean?

Switcheroo

I think the notation Σ O(i) indicates that we're re-using the constant for the big O, while O(1)+O(2)+...+O(n) has separate constants (this looks equivalent to Steve's interpretation). – Sucy

Answer 1

I think they're saying that when they use that notation (sum of a big-O), it means there's a single O(i) function (call it f(i)), and then the expression refers to the sum from 1 to n of that function.

This isn't the same thing as if there were n different functions (call them f_1(i) to f_n(i)), each of which is O(i), and then the expression refers to the sum of f_1(1) + f_2(2) + ... + f_n(n). That latter thing is not what the notation means.

Over

Well, Σ O(i) means Σ f(i), but what is the class of the "single function"? O(?) Σ O(i) takes no information about this, I think this is as ambiguous as "O(1) + O(2) + ... + O(n)" mentioned in the book. – Epstein

@Epstein Σ O(i) <=> Σ f(i) for some f such that, f(x) ∊ O(x) (for all x) – Federal

Answer 2

i think you should understand "The number of anonymous functions in an expression is understood to be equal to the number of times the asymptotic notation appears" at first. it means if

 Σ (i=1 to n) O(i)

so anonymous functions is one equals to O(i) such as Σ (i=1 to n) f1(i)

and if Σ (i=1 to n) O(i)+O(i) anonymous functions should have two functions equals to O(i)+O(i) such as Σ (i=1 to n) f1(i)+f2(i)

Antidote

Answer 3

The following is according to my understanding:

The passage simply states that.

This is what everyone first understands and it is the correct understanding of that cryptic passage, but the problem is WHY?, since we all are used to expand the sigma notations in the usual (and correct) way as in the expression above.

It turns out there is an exception when it comes to asymptotic notations like , etc. Recall that these asymptotic notations are all rough approximations for some anonymous function; due to this fact (the passage intends to convey that), before you expand and compute those sigma notations containing some asymptotic notation, you must firstly

1. figure out/evaluate/find out exactly that anonymous function and

2. substitute it for the asymptotic notation in the sigma expression and

3. only then expand and compute the sigma notation.

Thus:

But now let’s suppose, for the sake of argument, that the expression

is valid. But immediately we will face a problem here: since each of O(1), O(2), O(3),…, O(n) has a different value within its parentheses (1, 2, etc) and each subsequent number within parentheses is bigger than the previous one, it appears that each of these Big-Os represent a different anonymous function and each of these different anonymous functions grow faster than the previous different function.

Handcrafted