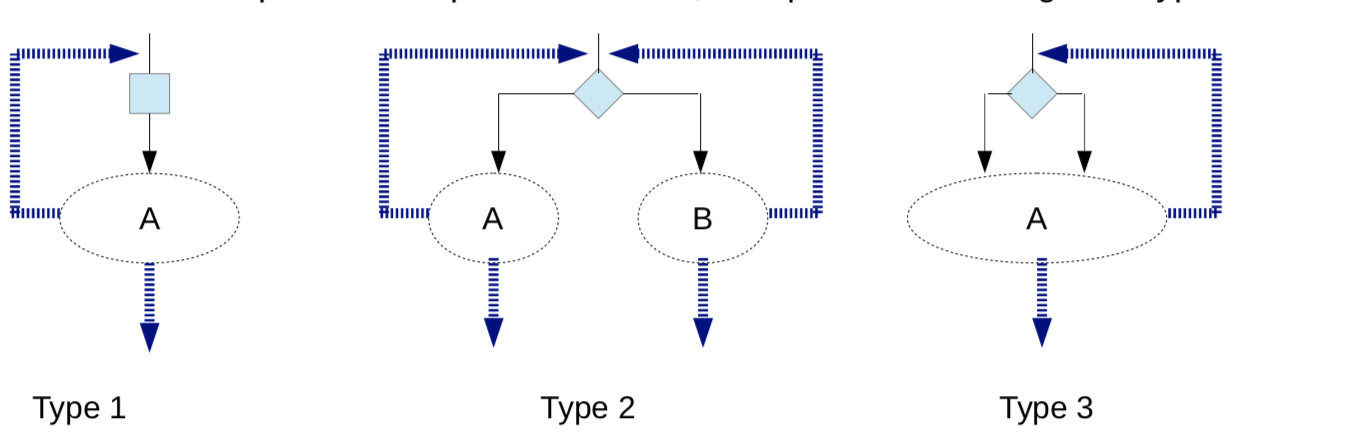
According to Böhm-Jacopini theorem, an algorithm can be written using only three statements:
- sequence
- selection
- iteration
Lots of teachers, assumes that theorem as an act of faith, and they teach to not use (goto, jump, break, multiple return, etc...) because these instructions are evil.
But when I ask for an explanation, no one is able to provide a proof of theorem.
Personally I don't think that the theorem is false, but I think that it's applicability in real world is not always the better choice.
So I've done a my little search, and these are my doubts:
The theorem has been proven on induction on the structure of the flow chart, but it's really applicable in a computer program?
According to wikipedia "Böhm and Jacopini's was not really practical as a program transformation algorithm, and thus opened the door for additional research in this direction".A consequence of theorem prove that each "goto" can be translated into selection or iteration by induction, but what about efficiency? I can't find any proof shows that each algorithm can be rewritten preserving the same performance.
Recursion, a recursive algorithm can really be written using only sequence, selection and iteration? I know that some recursive algorithms can be optimized as loops (think to tail recursion), but can really be applicable to all?
Clean code, I know that an abuse of jumps can create a monstrous code, but I think in some case a correct use of break in a loop can improve the code readability.
Sample:
n = 0;
while (n < 1000 || (cond1 && cond2) || (cond3 && cond4) || (cond5 && cond6))
{
n++;
//The rest of code
}
Can be rewritten as :
for (n = 0; n < 1000; n++)
{
if (cond1 && cond2) break;
elseif (cond2 && cond3) break;
elseif (cond4 && cond5) break;
elseif (cond6 && cond7) break;
//The rest of code
}
Personally I think that the theorem has not been created for write better code, and the idea that a clean code must follow this theorem has been spread into world for a strange subjective reason.
- I found this interesting article : https://www.cs.cornell.edu/~kozen/papers/bohmjacopini.pdf
I think this prove that real program must not be forced to follow the Jaopini Theorem.
Do you share the same conclusions?
Summarizing the question, I need to know if a program that uses only (sequence, selection and iteration) is really better than any other that uses different statements, and if there are proves or if it's all subjective.

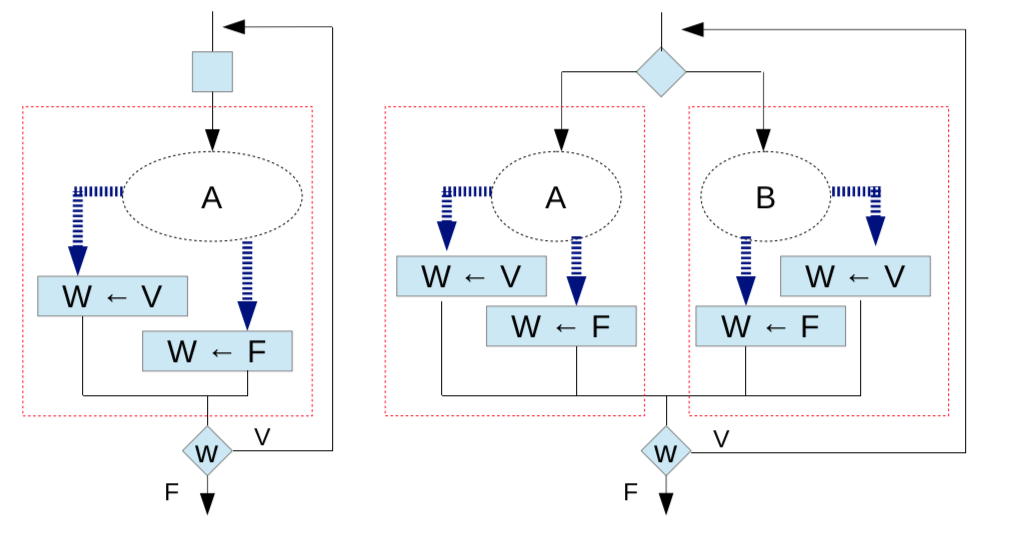
breakorcontinue) have a place but that Dijkstra has largely won the war. The Böhm-Jacopini theorem had little to do with it (beyond providing a response to those programmers who claimed that gotos were needed in an absolute sense). The success of structured programming is what convinced. – Annunciator