How would I efficiently find the min and max values of the variables in this constraint system?

Question

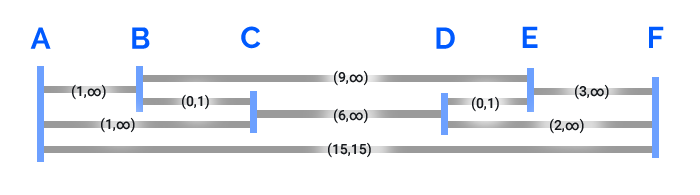
I have a system where I need to calculate the possible range of values for each variable (I don't need to find a solution to the system). Here is an illustration of an example system:

Each blue line is a node (named by the label above it), and the gray lines are the edges between the nodes. There is an initial constraint given: for example, edge BC can be any real number between 0 and 1 inclusive, and edge BE can be any number greater than or equal to 9. The nodes can't cross over other nodes. It's helpful to imagine them as metal bars that can extend and retract, pushing the blue plates around.

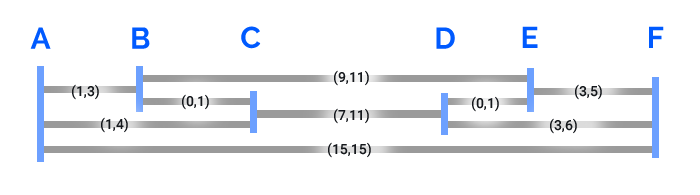
My goal is to calculate for each edge the minimum and maximum length they can be. The starting constraints set up the system, but the end result could be more constrained than them. For example, edge DF has a starting min/max of (2,∞), but you can see that it can't actually be shorter than 3, since contracting it pulls D into E, and E towards F, and EF has a minimum of 3. The end result would be this, I believe:

The caveat is I need an algorithm that can scale up to hundreds of thousands of nodes, which would be more densely connected than this example. It can't exponentially increase in running time, since I also have to run this algorithm hundreds of thousands of times.

I tried a method that gave some more constrained values, but not the most constrained values. To visualize the method, I essentially pulled all the plates over to the left as far as possible, then recorded each plates maximum position. Then I did the same, pulling them over to the right. Then, for each edge, I just find the difference between each plate's values. This method finds the maximum values very efficiently, but the problem is when you have a situation like in this example, where CD is sort of "locked" to BE by BC and DE. It can't be 6, since the system only allows it to be 2 shorter than 9. I need a way that finds the true min value of 7. My method doesn't capture that "locking" relationship: when you pull C all the way over to the left, BC is 0, and when you pull D all the way over to the right, DE is 0, but they can't both be 0 if CD is 6.

In this example, it's simple to see that CD is constrained by BE, but in practice, the system would be much denser and larger than the example, and finding such situations seems non-trivial. If the method involves searching around it locally, I'm worried it will scale poorly, but that may be the only way.

If this is modeled as a linear programming problem (AB + BC = AC, AB>1, etc), maybe there are some attributes of this system that could be taken advantage of: the fact that all the coefficients of the constraints are 1, and that there is only addition and subtraction in the constraints.

Does anyone have any suggestions on how to approach this problem? Or have any insights into what kind of run time complexity I should realistically hope for? Thanks!

Megathere

Answer 1

Okay, I think I've figured it out. Thanks to everyone who responded, it led me to some helpful research.

I was able to take advantage of the fact that I'm not running the algorithm on a different graph each time, but on the same one that is constantly being modified. I can keep the old values and update it each time, containing the updates to locally changed areas. The propagation shouldn't reach too far if the new changes aren't too drastic.

The algorithm is fairly intuitive. I was on the right track but I was missing the propagation step. It goes like this:

Look at the picture in question and imagine it as a physical system: there are blue plates with bars in between them that can contract and expand. To find the shortest a particular bar can be, I pull all of the plates all the way to the left, as much as possible. Keeping leftwards pressure on the bar's right plate, I pull its left plate towards it as much as I can. The movement propagates a change in position to all the bars connected to it. It can potentially move the right plate backwards a bit, which is fine. The energy of the movement gets consumed by the extra slack in the surrounding bars. Once the energy ripples through the system and settles down, I then record the final distance between the plates.

Finding the longest a bar can be is the same: I move the plates all the way to the left, then push the right plate away from the left as far as possible.

If I cache the positions from moving everything to the left and moving everything to the right, the values are helpful for quickly calculating the result. I can update these positions in a similar way when the graph is changed, keeping most of the work localized.

It's not technically linear, but with my data it is most of the time.

Megathere

Answer 2

Given

I need an algorithm that can scale up to hundreds of thousands of nodes, which would be more densely connected than this example. It can't exponentially increase in running time, since I also have to run this algorithm hundreds of thousands of times

you seem to be in trouble.

This looks like the following problem to me:

ICSP (Interval Constraint Satisfaction Problem). “Given a set E of equations relating a set of variables associated with interval domains. Refine the domains as far as possible without losing possible exact solutions of E, i.e., determine for each variable the minimal consistent subinterval within its domain.”

with some assumptions on E (linear inequalities). It's hard to read out what kind of implied bounds you are looking for (numerical vs. integral) and this might have a huge effect.

While this looks like a polynomial-time problem (hard to grasp the cycle/non-convergence properties without doing more research; see ref-paper; probably linked to floating-point math limitations vs. interval-arithmetic), those approaches probably won't scale for your numbers.

Take a look at

Belotti, Pietro, et al. "On feasibility based bounds tightening." (2012).

which gives some overview.

You will find a lot of keywords leading to different research-communities (Mathematical Optimization, Constraint Programming, AI) like:

• Feasibility-based bounds tightening
• bounds propagation
• bound/range reduction
• domain filtering/reduction.

There is a simple 2n LP-solving approach, but given your numbers, this will be not enough it seems, no matter if Simplex- or Interior-point methods are used.

The paper also introduces a single-LP approach, but it probably won't scale.

Depending on how important this problem is for you, how much you want to invest and what's your exact goal if a global-opt is infeasible (given some time-horizon), you might look into that paper, it's references and keywords and probably check out what's inside mathematical-optimization solvers including (links are pointing towards this core-problem):

• Couenne (which is somewhat linked to the paper; although the method implemented might be different than the paper)
• SCIP
  • (license! -> not for commercial usage)
• Clp

and others, where every one of those should include some bounds-tighetning approach (for linear equalities). In general, i would expect global-solvers like Couenne to be investing more time in this step; as the remaining optimization usually dominates this easily, compared to LP-solvers like Clp.

Caducous

Answer 3

It sounds like Satisfiability Modulo Theory will be helpful here. Give your length constraints as initial axioms (i.e. 0 <= BC <= 1, etc.), with a theory that lets you add distances (i.e. AB + BC = AC for all A,B,C), and let an SMT solver compute the constraints it can infer from that. I wouldn't be suprised if the "optimal" constraints you are looking for were found in near-linear time, since they seem to be pretty easy to infer.

Note however that SMT solvers are built with SAT in mind, which is NP-hard, so you wouldn't have any sub-exponential theoretical guarantees on running time. If what you need is actual running time to be acceptable, actual SMT solvers (with a hand-crafted stopping condition) would be my best guess, because they are very efficient in practice even though their worst-case complexity is exponential. If you also need theoretical guarantees on worst-case running time, I would suggest writing your own SMT-like proof generator and proving an upper bound on the number of non-redundant constraints that your model can generate, which also seems doable, but might turn out to be exponential.

You mentionned linear programming, and finding an instance that satisfies your constraints is indeed an LP problem. However, you are not interested here in the solution to the constraints, but in the actual optimaly-tightened constraints. This suggests that LP is not what you are looking for here (or not as-is at least). LP problems are of the form you mentionned but yield solutions that satisfy the given constraints, and it seems pretty hard to turn that back into constraints without exhaustively listing solutions, which you do not want. Satisfiability on the other hand, tries to deduce hidden constraints implied by the original constraints and hopes to find something that is not satisfiable (in which case it just returns UNSAT). If your constraints are indeed satisfiable, then the "hidden constraints" produced will be tighter than you original constraints, and you will only need to extract the subset of them that you are interested in.

That is why I would suggest digging into SMT rather than LP. Be aware though that this problem might be harder than it looks, as it seems to be possible to encode SAT in it, which would mean you'd have to pay exponential time for the worst case, but you'd perhaps be able to find approximate solutions in reasonable time, or ensure that average complexity is still acceptable.

Barnard

Answer 4

I think your problem is exactly the one of enforcing “Partial Path Consistency” on a “Simple Temporal Network”.

Simple Temporal Networks [1] are constraint networks with decision variables t_i (they correspond to your nodes/labels) and constraints of the form: L_ij <= t_j-t_i <= U_ij (where L_ij and U_ij are known bounds between some pairs of nodes, for instance in your example: 6<=D-C<=+oo). And the problem is to find the tightest bounds for each arc (so for each t_j-t_i) that is compatible with the constraints.

These problems have been heavily studied in temporal reasoning and scheduling.

In particular, your problem is polynomial. A simple method is to run a Floyd-Warshall algorithm to compute an all-pairs shortest path, as shown in [1]. But it will run in O(n^3) which is probably too expensive for you. There also exist more efficient algorithms, like for instance the one proposed in [2].

[1] Dechter, R.; Meiri, I.; and Pearl, J. 1991. Temporal constraint networks. Artificial Intelligence 49(1–3):61–95.

[2] Planken L. ; de Weerdt M.; and van der Krogt R. P3C: A New Algorithm for the Simple Temporal Problem. Proceedings of the Eighteenth International Conference on Automated Planning and Scheduling (ICAPS 2008).

Of course if you are only interested in the consistency of the constraint network, or in finding a feasible value for your nodes satisfying the constraints, the problem is much easier. Same thing if you only want to compute the tightest possible bounds for the nodes (as opposed to the arcs).

Crooked