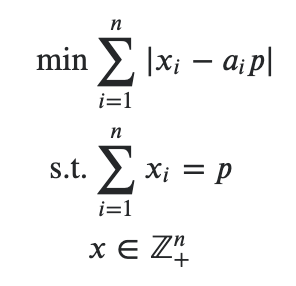I am working on a project where I need to breakdown an integer value according to an array of percentage values. My end array must contain integer value and the sum of the array must be equal to the initial integer.
Below is a fake example. We have a list of cars with some "potentials" and we need to allocate this potential to a specific postal code. the postal code allocation is dictated by some sellout information.
SELLOUTS_PER_P_CODE is dictating the weight to be put for each postal code allocation. For example, for the first car (car 1), there is a lot of weight for p_code_3 and less for p_code_2 and even less for p_code_1 so the allocation should be respectively for car 1 p_code_1=1, p_code_2=2, p_code_3=4.
Bellow is the mathematical form of the problem.
Here I am implementing this formulation using pyomo however it doesn't produce the expected result. The model doesn't take into consideration the weight factor from SELLOUTS_PER_P_CODE
from pyomo.environ import *
from pprint import pprint
def distribute(total, weights):
scale = float(sum(weights.values())) / total
return {k: v / scale for k, v in weights.items()}
Cars = ["car 1", "car 2", "car 3"]
Locations = ["p_code_1", "p_code_2", "p_code_3"]
POTENTIALS = {"car 1": 7, "car 2": 2, "car 3": 14}
SELLOUTS = {"p_code_1": 0.2, "p_code_2": 0.3, "p_code_3": 0.5}
SELLOUTS_PER_P_CODE = {}
for car in Cars:
pot = POTENTIALS[car]
scaled_sellout = distribute(pot, SELLOUTS)
t = {(car, p_code): v for p_code, v in scaled_sellout.items()}
SELLOUTS_PER_P_CODE.update(t)
pprint(SELLOUTS_PER_P_CODE)
model = ConcreteModel(name="Breakdown Potential to Postal Code")
model.Cars = Set(initialize=Cars)
model.Locations = Set(initialize=Locations)
model.a = Param(model.Cars, model.Locations, initialize=SELLOUTS_PER_P_CODE)
model.p = Param(model.Cars, initialize=POTENTIALS)
model.X_pos = Var(model.Cars, model.Locations, within=NonNegativeIntegers)
model.X_neg = Var(model.Cars, model.Locations, within=NonNegativeIntegers)
def objective_rule(model):
return sum(
(model.X_pos[i, j] - model.a[i, j] * model.p[i])
- (model.X_neg[i, j] - model.a[i, j] * model.p[i])
for i in model.Cars
for j in model.Locations
)
model.objective = Objective(rule=objective_rule, sense=minimize)
def sum_maintained_rule(model, i):
return (
sum(model.X_pos[i, j] for j in model.Locations)
+ sum(model.X_neg[i, j] for j in model.Locations)
== model.p[i]
)
model.sum_maintained = Constraint(model.Cars, rule=sum_maintained_rule)
def pyomo_postprocess(options=None, instance=None, results=None):
model.pprint()
if __name__ == "__main__":
opt = SolverFactory("glpk")
results = opt.solve(model)
results.write()
print("\nDisplaying Solution\n" + "-" * 80)
pyomo_postprocess(None, model, results)
And finally here is the incorrect output. Notice X_neg and X_pos for the output allocation.
Displaying Solution
--------------------------------------------------------------------------------
5 Set Declarations
Cars : Dim=0, Dimen=1, Size=3, Domain=None, Ordered=False, Bounds=None
['car 1', 'car 2', 'car 3']
Locations : Dim=0, Dimen=1, Size=3, Domain=None, Ordered=False, Bounds=None
['p_code_1', 'p_code_2', 'p_code_3']
X_neg_index : Dim=0, Dimen=2, Size=9, Domain=None, Ordered=False, Bounds=None
Virtual
X_pos_index : Dim=0, Dimen=2, Size=9, Domain=None, Ordered=False, Bounds=None
Virtual
a_index : Dim=0, Dimen=2, Size=9, Domain=None, Ordered=False, Bounds=None
Virtual
2 Param Declarations
a : Size=9, Index=a_index, Domain=Any, Default=None, Mutable=False
Key : Value
('car 1', 'p_code_1') : 1.4000000000000001
('car 1', 'p_code_2') : 2.1
('car 1', 'p_code_3') : 3.5
('car 2', 'p_code_1') : 0.4
('car 2', 'p_code_2') : 0.6
('car 2', 'p_code_3') : 1.0
('car 3', 'p_code_1') : 2.8000000000000003
('car 3', 'p_code_2') : 4.2
('car 3', 'p_code_3') : 7.0
p : Size=3, Index=Cars, Domain=Any, Default=None, Mutable=False
Key : Value
car 1 : 7
car 2 : 2
car 3 : 14
2 Var Declarations
X_neg : Size=9, Index=X_neg_index
Key : Lower : Value : Upper : Fixed : Stale : Domain
('car 1', 'p_code_1') : 0 : 7.0 : None : False : False : NonNegativeIntegers
('car 1', 'p_code_2') : 0 : 0.0 : None : False : False : NonNegativeIntegers
('car 1', 'p_code_3') : 0 : 0.0 : None : False : False : NonNegativeIntegers
('car 2', 'p_code_1') : 0 : 2.0 : None : False : False : NonNegativeIntegers
('car 2', 'p_code_2') : 0 : 0.0 : None : False : False : NonNegativeIntegers
('car 2', 'p_code_3') : 0 : 0.0 : None : False : False : NonNegativeIntegers
('car 3', 'p_code_1') : 0 : 14.0 : None : False : False : NonNegativeIntegers
('car 3', 'p_code_2') : 0 : 0.0 : None : False : False : NonNegativeIntegers
('car 3', 'p_code_3') : 0 : 0.0 : None : False : False : NonNegativeIntegers
X_pos : Size=9, Index=X_pos_index
Key : Lower : Value : Upper : Fixed : Stale : Domain
('car 1', 'p_code_1') : 0 : 0.0 : None : False : False : NonNegativeIntegers
('car 1', 'p_code_2') : 0 : 0.0 : None : False : False : NonNegativeIntegers
('car 1', 'p_code_3') : 0 : 0.0 : None : False : False : NonNegativeIntegers
('car 2', 'p_code_1') : 0 : 0.0 : None : False : False : NonNegativeIntegers
('car 2', 'p_code_2') : 0 : 0.0 : None : False : False : NonNegativeIntegers
('car 2', 'p_code_3') : 0 : 0.0 : None : False : False : NonNegativeIntegers
('car 3', 'p_code_1') : 0 : 0.0 : None : False : False : NonNegativeIntegers
('car 3', 'p_code_2') : 0 : 0.0 : None : False : False : NonNegativeIntegers
('car 3', 'p_code_3') : 0 : 0.0 : None : False : False : NonNegativeIntegers
1 Objective Declarations
objective : Size=1, Index=None, Active=True
Key : Active : Sense : Expression
None : True : minimize : X_pos[car 1,p_code_1] - 9.8 - (X_neg[car 1,p_code_1] - 9.8) + X_pos[car 1,p_code_2] - 14.700000000000001 - (X_neg[car 1,p_code_2] - 14.700000000000001) + X_pos[car 1,p_code_3] - 24.5 - (X_neg[car 1,p_code_3] - 24.5) + X_pos[car 2,p_code_1] - 0.8 - (X_neg[car 2,p_code_1] - 0.8) + X_pos[car 2,p_code_2] - 1.2 - (X_neg[car 2,p_code_2] - 1.2) + X_pos[car 2,p_code_3] - 2.0 - (X_neg[car 2,p_code_3] - 2.0) + X_pos[car 3,p_code_1] - 39.2 - (X_neg[car 3,p_code_1] - 39.2) + X_pos[car 3,p_code_2] - 58.800000000000004 - (X_neg[car 3,p_code_2] - 58.800000000000004) + X_pos[car 3,p_code_3] - 98.0 - (X_neg[car 3,p_code_3] - 98.0)
1 Constraint Declarations
sum_maintained : Size=3, Index=Cars, Active=True
Key : Lower : Body : Upper : Active
car 1 : 7.0 : X_pos[car 1,p_code_1] + X_pos[car 1,p_code_2] + X_pos[car 1,p_code_3] + X_neg[car 1,p_code_1] + X_neg[car 1,p_code_2] + X_neg[car 1,p_code_3] : 7.0 : True
car 2 : 2.0 : X_pos[car 2,p_code_1] + X_pos[car 2,p_code_2] + X_pos[car 2,p_code_3] + X_neg[car 2,p_code_1] + X_neg[car 2,p_code_2] + X_neg[car 2,p_code_3] : 2.0 : True
car 3 : 14.0 : X_pos[car 3,p_code_1] + X_pos[car 3,p_code_2] + X_pos[car 3,p_code_3] + X_neg[car 3,p_code_1] + X_neg[car 3,p_code_2] + X_neg[car 3,p_code_3] : 14.0 : True
11 Declarations: Cars Locations a_index a p X_pos_index X_pos X_neg_index X_neg objective sum_maintained