You can calculate it using python Decimal built-in module to control how many decimals (https://docs.python.org/2/library/decimal.html) you are going to use.
a = 1/7
len(str(a))-2
Out[1] 17
using Decimal:
from decimal import *
getcontext().prec = 90 #90 decimals precision
a = Decimal(1) / Decimal(7)
len(str(a))-2
Out[2] 90
basically:
n = 100000
Euler_Mascheroni = -Decimal(log(Decimal(n))) + sum([Decimal(1)/Decimal(i) for i in range(1,n)])
Euler_Mascheroni
Out[3] Decimal('0.577210664893199330073570099082905499710324918344701101627529415938181982282214')
finally, you can "arbitrarily" increase precision:
from decimal import *
from math import log
def Euler_Mascheroni(n,nth_decimals = 80):
getcontext().prec = nth_decimals
SUM = Decimal(0)
for i in range(1,n):
SUM+=Decimal(1)/Decimal(i)
return -Decimal(log(Decimal(n))) + SUM
Euler_Mascheroni(100000000,nth_decimals = 120)
which gives:
Decimal('0.5772156599015311156682000509495086978690376512201034388184221886576113026091829254475798266636558124658249350393045066')
Answering comment from @Stef
EM = Decimal(0.57721566490153286060651209008240243104215933593992)#reference taken from wikipedia
n = 100000000
Decimal(log(Decimal(n)))
getcontext().prec = 100
SUM = Decimal(0)
for i in range(1,n):
SUM+=Decimal(1)/Decimal(i)
EM - (SUM-Decimal(log(Decimal(n))))
will give
Decimal('5.00000174 ... 85E-9')

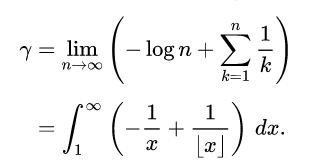
decimalmodule is the way to go. – Heroinfractionsmodule if you want to compute the value yourself. This would alleviate the need to pick a specific decimal precision. – Knudson