Check polygon intersection in R: sf::intersects incorrectly returns TRUE result while rgeos::gIntersects correctly returns FALSE

Question

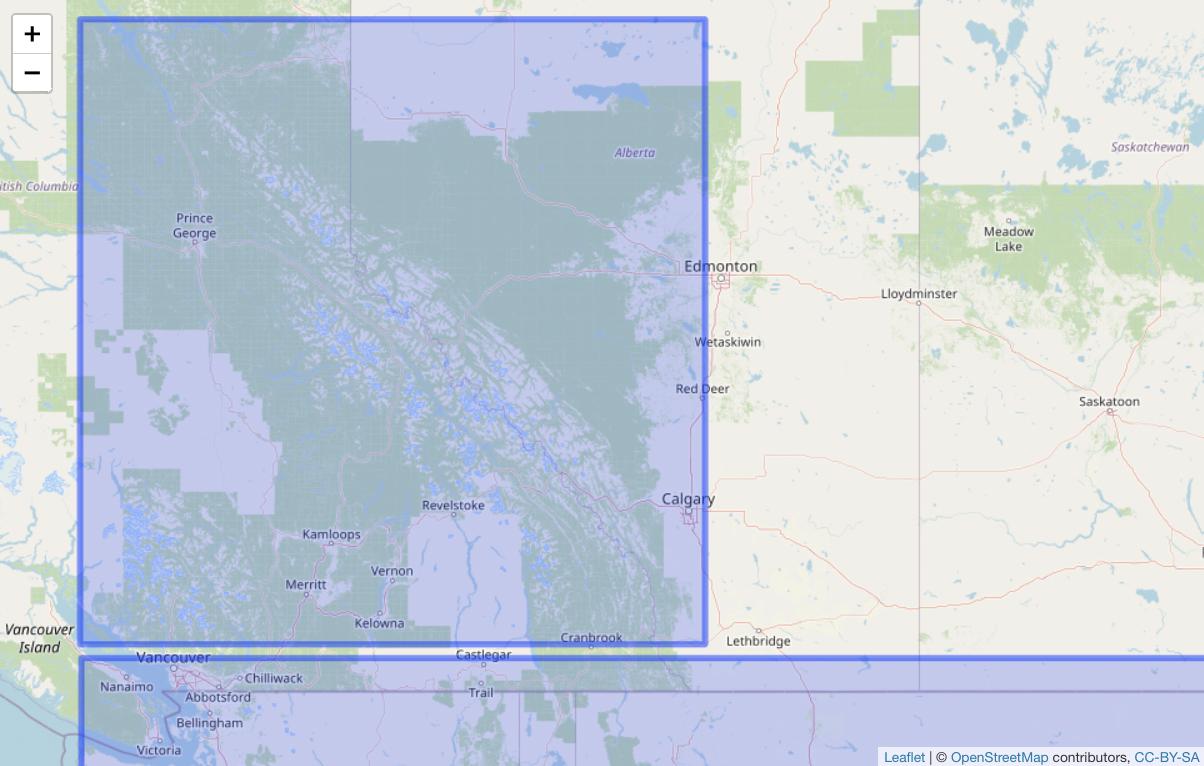
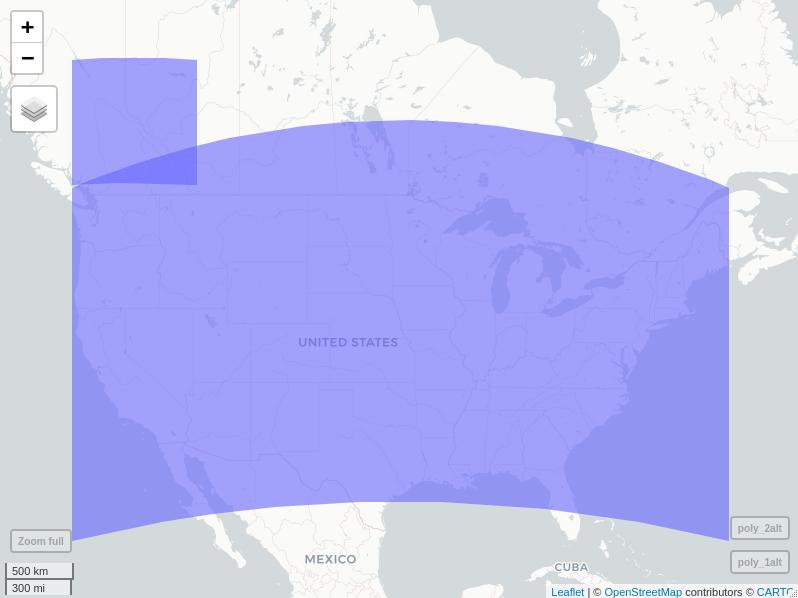
I'm trying to check whether two polygons intersect in R. When plotting, they clearly do not. When checking the intersection, rgeos::gIntersects() currently returns FALSE, while sf::intersects() returns TRUE. I imagine this is due to the polygons being (1) large and (2) close together, so something about when on a flat surface they don't appear to intersect but on a sphere they would appear to intersect?

Ideally I could keep my workflow all in sf -- but I'm wondering if there's a way to use sf::intersects() (or another sf function) that will return FALSE here?

Here's an example:

library(sf)
library(rgeos)
library(leaflet)
library(leaflet.extras)

#### Make Polygons
poly_1 <- c(xmin = -124.75961, ymin = 49.53330, xmax = -113.77328, ymax = 56.15249) %>% 
  st_bbox() %>%
  st_as_sfc()
st_crs(poly_1) <- 4326

poly_2 <- c(xmin = -124.73214, ymin = 25.11625, xmax = -66.94889, ymax = 49.38330) %>% 
  st_bbox() %>%
  st_as_sfc()
st_crs(poly_2) <- 4326

#### Plotting
# Visually, the polygons do not intersect
leaflet() %>%
  addTiles() %>%
  addPolygons(data = poly_1) %>%
  addPolygons(data = poly_2)

#### Check Intersection
# returns FALSE
gIntersects(poly_1 %>% as("Spatial"), 
            poly_2 %>% as("Spatial"))

# returns TRUE
st_intersects(poly_1,
              poly_2,
              sparse = F)

Here's the polygons, which visually do not intersect.

Polynuclear

Answer 1

This is an interesting problem, with the root cause being difference between planar (on a flat surface) and spherical (on a globe) geometry.

On a plane - which is a simplified approach that GEOS takes - the four corners of a polygon are connected by four straight lines, the sum of angles is 360° degrees etc. Geometry works as Euclid taught ages ago.

But, and this is crucial, this is not how the world works. On a globe the four connections of polygon are not straight lines but great circles. Or rather they are straight when drawn on a globe, and curved when rolled flat one a planar surface (such as a map or your computer screen).

Because an example is more than a 1000 words consider this piece of code:

library(sf)
library(dplyr)

# make polygons
poly_1 <- c(xmin = -124.75961, ymin = 49.53330, xmax = -113.77328, ymax = 56.15249) %>% 
  st_bbox() %>%
  st_as_sfc()
st_crs(poly_1) <- 4326

poly_2 <- c(xmin = -124.73214, ymin = 25.11625, xmax = -66.94889, ymax = 49.38330) %>% 
  st_bbox() %>%
  st_as_sfc()
st_crs(poly_2) <- 4326

# this is what you *think* you see (and what GEOS sees, being planar) 
# = four corners connected by straight lines
# & no intersecton
mapview::mapview(list(poly_1, poly_2))

# this is what you *should* see (and what {s2} sees, being spherical)
# = four corners connected by great circles
# & an obvious intersection around the lower right corner of the small polygon
poly_1alt <- st_segmentize(poly_1, units::set_units(1, degree))
poly_2alt <- st_segmentize(poly_2, units::set_units(1, degree))

mapview::mapview(list(poly_1alt, poly_2alt))

You have two options:

• accept that your thinking about polygons was wrong, and embrace spherical, i.e. {s2} logic.

This should be in theory the correct approach, but somewhat counter intuitive.

• make {sf} abandon spherical approach to polygons, and force it to apply planar approach (such as GEOS uses).

This would be in theory a wrong approach, but consistent both with your planar intuition and previous behaviour of most GIS tools, including {sf} prior to version 1.0.0

# remedy (of a kind...) = force planar geometry operations

sf::sf_use_s2(FALSE)

st_intersects(poly_1, poly_2, sparse = F)
#      [,1]
# [1,] FALSE

Wester

I'd take issue with your idea that one is "correct" here. Correctness only makes sense within some greater framework and if your framework is that lat-long is a cartesian coordinate system then the great circles are wrong. I'm sure there are regulatory standards where this is true (think of borders being defined along lines of latitude, for example). – Klaipeda

@Klaipeda I definitely agree that "correctness" is a slippery term. In general we tend to think of Earth as a sphere, and laugh at the flat earthers - but this has consequences of non-Euclidean geometry that we often find difficult to work with. Even our tools are not quite consistent - like how come that segmentizing a polygon changes its shape? The points should lie on the original line from the very beginning. – Wester

This is really surprising to me, in the other direction. My "intuition" is that making a polygon with a bbox that way should result in great circles already. What is the "right" way to say, I want to fill in a "box" that curves along a particular latitude line? – Broderickbrodeur