Algorithm: Check if max flow is unique

Question

A question to the following exercise:

Let N = (V,E,c,s,t) be a flow network such that (V,E) is acyclic, and let m = |E|. Describe a polynomial- time algorithm that checks whether N has a unique maximum flow, by solving ≤ m + 1 max-flow problems. Explain correctness and running time of the algorithm

My suggestion would be the following:

run FF (Ford Fulkerson) once and save the value of the flow v(f) and the flow over all egdes f(e_i)
for each edge e_i with f(e_i)>0:
    set capacity (in this iteration) of this edge c(e_i)=f(e_i)-1 and run FF. 
    If the value of the flow is the same as in the original graph, then there exists another way to push the max flow through the network and we're done - the max flow isn't unique --> return "not unique"
    Otherwise we continue 

we're done with looping without finding another max flow of same value, that means max flow is unique -> return "unique"

Any feedback? Have I overlooked some cases where this does not work?

Fischer

Answer 1

Your question leaves a few details open, e.g., is this an integer flow graph (probably yes, although Ford-Fulkerson, if it converges, can run on other networks as well), and how exactly do you define whether two flows are different (is it enough that the function mapping edges to flows be different, or must the set of edges actually flowing something be different, which is a stronger requirement).

---

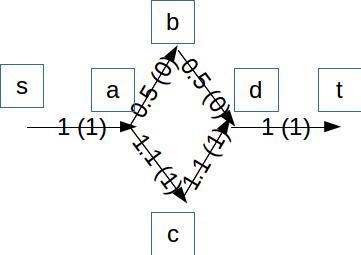
If the network is not necessarily integer flows, then, no, this will not necessarily work. Consider the following graph, where, on each edge, the number within the parentheses represents the actual flow, and the number to the left of the parentheses represents the capacity (e.g., the capacity of each of (a, c) and (c, d) is 1.1, and the flow of each is 1.):

In this graph, the flow is non-unique. It's possible to flow a total of 1 by floating 0.5 through (a, b) and (b, d). Your algorithm, however, won't find this by reducing the capacity of each of the edges to 1 below its current flow.

---

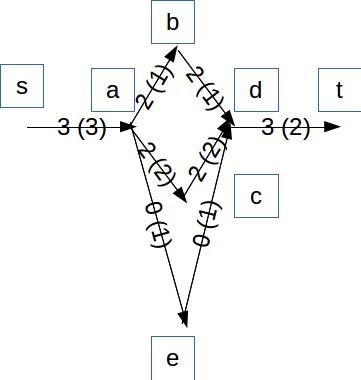
If the network is integer, it is not guaranteed to find a different set of participating edges than the current one. You can see it through the following graph:

---

Finally, though, if the network is an integer flow network, and the meaning of a different flow is simply a different function of edges to flows, then your algorithm is correct.

1. Sufficiency If your algorithm finds a different flow with the same total result, then obviously the new flow is legal, and, also, necessarily, at least one of the edges is flowing a different amount than it did before.

2. Necessity Suppose there is a different flow than the original one (with the same total value), with at least one of the edges flowing a different amount. Say that, for each edge, the flow in the alternative solution is not less than the flow in the original solution. Since the flows are different, there must be at least a single edge where the flow in the alternative solution increased. Without a different edge decreasing the flow, though, there is either a violation of the conservation of flow, or the original solution was suboptimal. Hence there is some edge e where the flow in the alternative solution is lower than in the original solution. Since it is an integer flow network, the flow must be at least 1 lower on e. By definition, though, reducing the capacity of e to at least 1 lower than the current flow, will not make the alternative flow illegal. Hence some alternative flow must be found if the capacity is decreased for e.

Genniegennifer

thank you for this detailed answer! As the two points mentioned (integer flow, meaning of different flow) are not further defined in the exercise, it should be sufficient that the algorithm works with those assumptions/simplifications made. – Fischer

@Fischer You also probably need to include in your proof a short mention that the resulting algorithm is indeed polynomial (because its time complexity is O(|E| * C), where C is the complexity of Ford-Fulkerson). – Rachele

Nice proof, but what happens if the algorithm returns False? You must prove that there is only one unique flow function in that case. – Patrilocal

Answer 2

• non integer, rational flows can be 'scaled' to integer
• changing edges capacity is risky, because some edges may be critical and are included in every max flow

there is a better runtime solution, you don't need to check every single edge. create a residual network (https://en.wikipedia.org/wiki/Flow_network). run DFS on the residual network graph, if you find a circle it means there is another max flow, wherein the flow on at least one edge is different.

Scheldt

This answer is incorrect! Suppose G consists of two edges s->v->t, where s->v has capacity 1 and v->t has capacity 2. G clearly has a unique maximum (s,t)-flow, with value 1. But the residual network of that flow has a cycle of length 2 through v and t. – Kilk