Determining High Density Region for a distribution in R

Question

Background:

Normally, R gives quantiles for well-known distributions. Out of these quantiles, the lower 2.5% up to the upper 97.5% covers 95% of the area under these distributions.

Question:

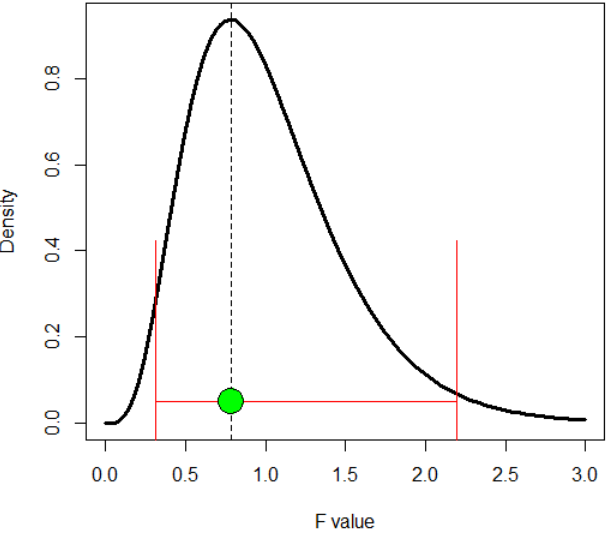
Suppose I have a F distribution (df1 = 10, df2 = 90). In R, how can I determine the 95% of the area under this distribution such that this 95% only covers the HIGH DENSITY area, not the 95% that R normally gives (see my R code Below)?

Note: Clearly, the highest density is the "mode" (dashed line in the pic below). So I guess, one must move from "mode" toward the tails.

Here is my R code:

curve(df(x, 10, 90), 0, 3, ylab = 'Density', xlab = 'F value', lwd = 3)

Mode = ( (10 - 2) / 10 ) * ( 90 / (90 + 2) )

abline(v = Mode, lty = 2)

CI = qf( c(.025, .975), 10, 90)

arrows(CI[1], .05, CI[2], .05, code = 3, angle = 90, length = 1.4, col= 'red' )

points(Mode, .05, pch = 21, bg = 'green', cex = 3)

Transform

Answer 1

Section 25.2 of DBDA2E gives complete R code for determining highest density intervals for distributions specified three ways: as cumulative density functions, as grid approximations, or as samples. For a cumulative density function, the function is called HDIofICDF(). It's in the utilities script, DBDA2E-utilities.R at the book's web site (linked above). Here's the code:

HDIofICDF = function( ICDFname , credMass=0.95 , tol=1e-8 , ... ) {
  # Arguments:
  # ICDFname is R’s name for the inverse cumulative density function
  # of the distribution.
  # credMass is the desired mass of the HDI region.
  # tol is passed to R’s optimize function.
  # Return value:
  # Highest density interval (HDI) limits in a vector.
  # Example of use: For determining HDI of a beta(30,12) distribution, type
  # > HDIofICDF( qbeta , shape1 = 30 , shape2 = 12 )
  # Notice that the parameters of the ICDFname must be explicitly named;
  # e.g., HDIofICDF( qbeta , 30 , 12 ) does not work.
  # Adapted and corrected from Greg Snow’s TeachingDemos package.
  incredMass = 1.0 - credMass
  intervalWidth = function( lowTailPr , ICDFname , credMass , ... ) {
    ICDFname( credMass + lowTailPr , ... ) - ICDFname( lowTailPr , ... )
  }
  optInfo = optimize( intervalWidth , c( 0 , incredMass ) , ICDFname=ICDFname ,
    credMass=credMass , tol=tol , ... )
  HDIlowTailPr = optInfo$minimum
  return( c( ICDFname( HDIlowTailPr , ... ) ,
    ICDFname( credMass + HDIlowTailPr , ... ) ) )
}

Indigence

Yes, it works for any icdf function, but it does assume a unimodal pdf. – Indigence

Answer 2

Have you tried this package: https://github.com/robjhyndman/hdrcde ?

Following your exemple:

library(hdrcde)
hdr.den(rf(1000,10,90),prob=95)

You can use various High Density Region and it works well for mulitmodal pdf.

hdr.den(c(rf(1000,10,90),rnorm(1000,4,1)),prob=c(50,75,95))

And

And you can even use it with multivariate distribution to visual 2D high density regions:

hdrs=c(50,75,95)
x=c(rf(1000,10,90),rnorm(1000,4,1))
y=c(rf(1000,5,50),rnorm(1000,7,1) )
par(mfrow=c(1,3))
hdr.den(x,prob=hdrs,xlab="x")
hdr.den(y,prob=hdrs,xlab="y")
hdr.boxplot.2d(x,y,prob=hdrs,shadecol="red",xlab="x",ylab="y")

Kalmick

Answer 3

Use the HDR.f function in the stat.extend package

The stat.extend package gives HDR functions for all the base distributions in R and some distributions in its extension packages. It uses methods based on the quantile functions for the distributions, and automatically adjusts for the shape of the distribution (unimodal, bimodal, etc.). Here is how to use the function to compute the HDR of interest to you.

#Load library
library(stat.extend)

#Compute HDR for an F distribution
HDR.f(cover.prob = 0.9, df1 = 10, df2 = 20)

        Highest Density Region (HDR) 
 
90.00% HDR for F distribution with 10 numerator degrees-of-freedom and 
20 denominator degrees-of-freedom 
Computed using nlm optimisation with 9 iterations (code = 3) 

[0.220947190373167, 1.99228812929142]

Densimeter