Create triangular mesh from vertex coordinates

Question

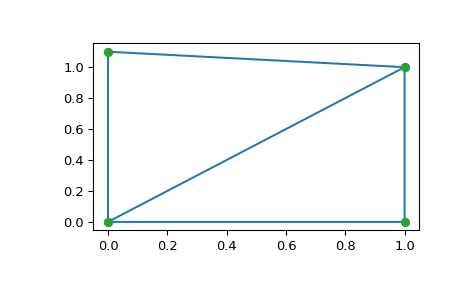
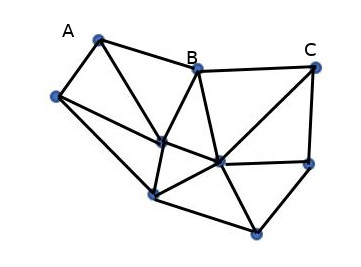
Given a set of 2d data points with coordinates x and y (left picture), is there an easy way to construct a triangular mesh on top of it (right picture)? i.e. return a list of tuples that indicates which vertices are connected. The solution is not unique, but any reasonable mesh would suffice.

Phylum

Answer 1

You can try scipy.spatial.Delaunay. From that link:

points = np.array([[0, 0], [0, 1.1], [1, 0], [1, 1]])

from scipy.spatial import Delaunay

tri = Delaunay(points)

plt.triplot(points[:,0], points[:,1], tri.simplices)

plt.plot(points[:,0], points[:,1], 'o')

plt.show()

Output:

Compton

Answer 2

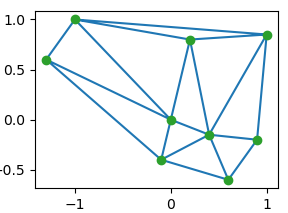
You can use scipy.spatial.Delaunay. Here is an example from the

import numpy as np
points = np.array([[-1,1],[-1.3, .6],[0,0],[.2,.8],[1,.85],[-.1,-.4],[.4,-.15],[.6,-.6],[.9,-.2]])
from scipy.spatial import Delaunay
tri = Delaunay(points)

import matplotlib.pyplot as plt
plt.triplot(points[:,0], points[:,1], tri.simplices)
plt.plot(points[:,0], points[:,1], 'o')
plt.show()

Here is the result on an input similar to yours:

The triangles are stored in the simplices attribute of the Delaunay object which reference the coordinates stored in the points attribute:

>>> tri.points
array([[-1.  ,  1.  ],
       [-1.3 ,  0.6 ],
       [ 0.  ,  0.  ],
       [ 0.2 ,  0.8 ],
       [ 1.  ,  0.85],
       [-0.1 , -0.4 ],
       [ 0.4 , -0.15],
       [ 0.6 , -0.6 ],
       [ 0.9 , -0.2 ]])
>>> tri.simplices
array([[5, 2, 1],
       [0, 3, 4],
       [2, 0, 1],
       [3, 0, 2],
       [8, 6, 7],
       [6, 5, 7],
       [5, 6, 2],
       [6, 3, 2],
       [3, 6, 4],
       [6, 8, 4]], dtype=int32)

If you are looking for which vertices are connected, there is an attribute containing that info also:

>>> tri.vertex_neighbor_vertices
(array([ 0,  4,  7, 12, 16, 20, 24, 30, 33, 36], dtype=int32), array([3, 4, 2, 1, 5, 2, 0, 5, 1, 0, 3, 6, 0, 4, 2, 6, 0, 3, 6, 8, 2, 1,
       6, 7, 8, 7, 5, 2, 3, 4, 8, 6, 5, 6, 7, 4], dtype=int32))

Addlebrained

Answer 3

I think Delanuay gives something closer to a convex hull. In OP's picture A is not connected to C, it is connected to B which is connected to C which gives a different shape.

One solution could be running Delanuay first then removing triangles whose angles exceed a certain degree, eg 90, or 100. A prelim code could look like

from scipy.spatial import Delaunay
points = [[101, 357], [198, 327], [316, 334], [ 58, 299], [162, 258], [217, 240], [310, 236], [153, 207], [257, 163]]
points = np.array(points)

tri = Delaunay(points,furthest_site=False)
newsimp = []
for t in tri.simplices:
  A,B,C = points[t[0]],points[t[1]],points[t[2]]
  e1 = B-A; e2 = C-A
  num = np.dot(e1, e2)
  denom = np.linalg.norm(e1) * np.linalg.norm(e2)
  d1 = np.rad2deg(np.arccos(num/denom))
  e1 = C-B; e2 = A-B
  num = np.dot(e1, e2)
  denom = np.linalg.norm(e1) * np.linalg.norm(e2)
  d2 = np.rad2deg(np.arccos(num/denom))
  d3 = 180-d1-d2
  degs = np.array([d1,d2,d3])
  if np.any(degs > 110): continue
  newsimp.append(t)

plt.triplot(points[:,0], points[:,1], newsimp)

which gives the shape seen above. For more complicated shapes removing large sides could be necessary too,

for t in tri.simplices:
  ...
  n1 = np.linalg.norm(e1); n2 = np.linalg.norm(e2)
  ...
  res.append([n1,n2,d1,d2,d3])

res = np.array(res)
m = res[:,[0,1]].mean()*res[:,[0,1]].std()

mask = np.any(res[:,[2,3,4]] > 110) & (res[:,0] < m) & (res[:,1] < m )

plt.triplot(points[:,0], points[:,1], tri.simplices[mask])

Beware

Ordinarily, the Delaunay gives rise to a bounding polygon that is convex (a convex hull). From time-to-time, there's been some discussion of on Stackoverflow about "alpha shapes" for the Delaunay. An alpha shape permits concavities. So you might try a search on "delaunay alpha" and see if anything that you find is applicable to your problem. – Kings

That alpha shapes approach doesn't work all the time. I think you are better off sticking to a triangulation mesh generation approach, that can help you further down the line with compsci code. This is an active area of research, how to make Delanuay work better for FEM for instance. – Beware