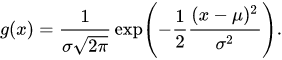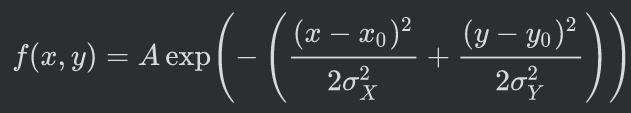How to create a normal 2d distribution in pytorch

Question

Given a tensor containing N points, represented in [x,y], I want to create a 2D gaussian distribution around each point, draw them on an empty feature map.

For example, the left image shows one given point (registered as a pixel on the feature map, whose value is set to 1). The right image adds a 2D guassian distribution around it.

How could I add such distribution for each point? Is there an API for it in pytorch?

Durwyn

Answer 1

Sampling from the multivariate normal distribution

You can use MultivariateNormal to sample from a multivariate normal.

>>> h, w = 200, 200
>>> fmap = torch.zeros(h, w)

Fill fmap with the origin points:

>>> pts = torch.rand(20, 2)
>>> pts *= torch.tensor([h, w])
>>> x, y = pts.T.long()
>>> x, y = x.clip(0, h), y.clip(0, w)

>>> fmap[x, y] = 1

Following this, we can sample from the following distribution (you can adjust the covariance matrix accordingly):

>>> sampler = MultivariateNormal(pts.T, 10*torch.eye(len(pts)))

>>> for x in range(10):
...    x, y = sampler.sample()
...    x, y = x.clip(0, h).long(), y.clip(0, w).long()
...    fmap[x, y] = 1

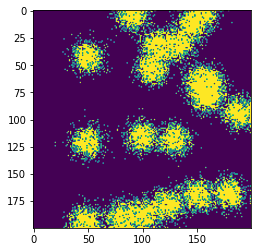
As a result, you can end up with something like:

Origin points	Normal sampling

This is not documented well enough, but you can pass the sample shape to the sample function. This allows you to sample multiple points per call, i.e. you only need one to populate your canvas.

Here is a function to draw from MultivariateNormal:

def multivariate_normal_sampler(mean, cov, k):
    sampler = MultivariateNormal(mean, cov)
    return sampler.sample((k,)).swapaxes(0,1).flatten(1)

Then you can call it as:

>>> x, y = multivariate_normal_sampler(mean=pts.T, cov=50*torch.eye(len(pts)), k=1000)

Clip the samples:

>>> x, y = x.clip(0, h-1).long(), y.clip(0, w-1).long()

Finally insert into fmap and draw:

>>> fmap[x, y] += .1

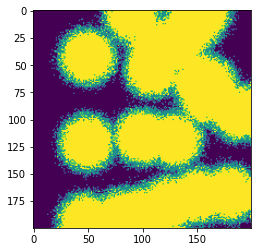
Here is an example preview:

k=1,000	k=50,000

_{The utility function is available as torch.distributions.multivariate_normal.MultivariateNormal}

---

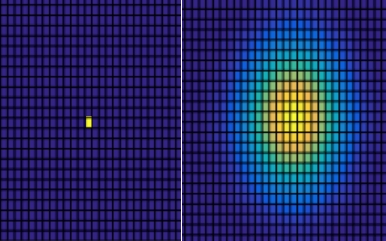
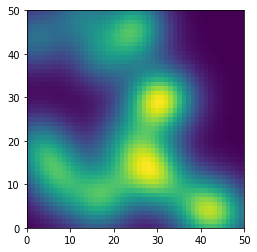
Computing the density map using the pdf

Alternatively, instead of sampling from the normal distribution, you could compute the density values based on its probability density function (pdf):

A particular example of a two-dimensional Gaussian function is:

Origin points:

>>> h, w = 50, 50
>>> x0, y0 = torch.rand(2, 20)
>>> origins = torch.stack((x0*h, y0*w)).T

Define the gaussian 2D pdf:

def gaussian_2d(x=0, y=0, mx=0, my=0, sx=1, sy=1):
    return 1 / (2*math.pi*sx*sy) * \
      torch.exp(-((x - mx)**2 / (2*sx**2) + (y - my)**2 / (2*sy**2)))

Construct the grid and accumulate the gaussians from each origin points:

x = torch.linspace(0, h, h)
y = torch.linspace(0, w, w)
x, y = torch.meshgrid(x, y)

z = torch.zeros(h, w)
for x0, y0 in origins:
  z += gaussian_2d(x, y, mx=x0, my=y0, sx=h/10, sy=w/10)

Multivariate normal distributions

_{The code to plot the grid of values is simply using matplotlib.pyplot.pcolormesh: plt.pcolormesh(x, y, z).}

Jovi

Thanks! My feature map is however not binary, could we assign float value (from 0 to 1) to each pixel near the given points? (instead of adding discrete points around) – Durwyn

use fmap[x, y] = 1 to fill all points is very elegant ! – Durwyn

Ps. To avoid the area between two close points having larger value than the points themselves, I used z= torch.max(z, gaussian_2d()) instead of z += gaussian_2d() – Durwyn