Find Faster R Computation for Iterative Matrix Computations

Question

I have the following code that lives inside an optimization routine. Hence, while it's reasonably fast, profiling shows the line producing the result called res to be the largest bottleneck in my code.

I have tried quite a few ways to improve this and have ended up with this final line:

res <- exp(X %*% log(pr.t) + mX %*% log(1 - pr.t)) %*% wts

In my problem, the elements of the matrix X are fixed and do not change over iterations. So, I can also compute, store and recycle both X and mX. What does change at each iteration are some probabilities I compute in the object pr.t.

I have tried Rcpp, but Rcpp was just as fast as this R code in my work.

I'm appealing now to this group to see if anyone sees a brilliant way to speed up the line producing the final object res. Sample code to set up the problem is below to give a reprodicible example of the real problem.

X <- matrix(sample(c(0,1), 5000, replace = TRUE), 1000, 5)
mX <- 1 - X
pr.t <- matrix(runif(75), 5, 15)
wts <- runif(15)
res <- exp(X %*% log(pr.t) + mX %*% log(1 - pr.t)) %*% wts

Petrography

Are X and mX always binary matrices? – Dalesman

Have you already experimented with optimized/parallelized BLAS, e.g. brettklamer.com/diversions/statistical/faster-blas-in-r ? – Rampage

I tried this with sparse matrices from Matrix: it doesn't seem to help in this case, even when I increase sparsity to 99%. As @Dalesman hints, an indexing-based solution might help? – Rampage

I get a factor of ~1.5 speed up by writing your code in C and a factor of ~3 speed up by writing your code in C and computing on the linear (instead of log) scale. An optimized BLAS might do better ... – Oof

@jblood94, yes, X and mX are always binary – Petrography

Answer 1

First, if nrow(X) is much larger than nrow(unique(X)), as in your example, you need only to compute the possible nrow(unique(X)) values of res and then index. This will reduce the size of the multiplications. Second, the exp, log and first two matrix multiplications can be replaced with a function that does the multiplications directly:

n <- ncol(X)
X0 <- unique(X)
mX0 <- 1 - X0 # only needed for `res2`
i <- match(X %*% 2^((n - 1):0), X0 %*% 2^((n - 1):0))
X02 <- collapse::setop(X0*n, "+", 1:n, rowwise = TRUE)
mode(X02) <- "integer"

f <- function(pr.t, wts) {
  pr.t2 <- rbind(1 - pr.t, pr.t)
  res <- pr.t2[X02[,1],]
  if (n != 1L) for (j in 2:n) res <- res*pr.t2[X02[,j],]
  (res %*% wts)[i,,drop = FALSE]
}

microbenchmark::microbenchmark(
  res = exp(X %*% log(pr.t) + mX %*% log(1 - pr.t)) %*% wts,
  res2 = (exp(X0 %*% log(pr.t) + mX0 %*% log1p(-pr.t)) %*% wts)[i,,drop = FALSE],
  res3 = f(pr.t, wts),
  check = "equal",
  unit = "relative"
)
#> Unit: relative
#>  expr       min        lq      mean    median        uq       max neval
#>   res 47.141593 44.735632 27.885564 40.779310 33.565934 7.1477733   100
#>  res2  2.088496  1.900383  1.317103  1.751724  1.483516 0.8380567   100
#>  res3  1.000000  1.000000  1.000000  1.000000  1.000000 1.0000000   100

Dalesman

Why are you using log1p(-pr.t) instead of log(1 - pr.t)? – Edibles

You should move your efforts of calculating index i also into res2 for fair comparison – Backstairs

@jblood94, this is a good working solution and I like the premise--make a big problem smaller. So to the degree that nrow(X0) << nrow(X), this reduces compute time in my real working code. As noted above, X and mX are always binary, so I'm curious if you see an additional way to exploit that. – Petrography

@ThomasIsCoding, since X is fixed, and i depends only on X, the benchmark shows the per iteration speed improvement for calculating i up front. – Dalesman

@jay.sf, log1p(-pr.t) will be slightly faster. Plus, it will maintain precision if pr.t is very small. Although, if pr.t can also get very close to 1, log1p(pr.t - 1) is safer than log(pr.t), which would negate any speed gains. – Dalesman

Sure, however check set.seed(563458); x <- -runif(1); identical(log(1 - x), log1p(-x)), might be a rounding issue but didn't go through the math. check = "identical" in benchmark might also fail. – Edibles

Sorry, I'm not seeing your point. I get TRUE for identical(log(1 - x), log1p(-x)). Try x <- 2^-54; xp <- Rmpfr::mpfr(x, 64); dput(c(log(1 - x), log1p(-x), as.numeric(log(1 - xp)))). – Dalesman

@dhc, see the updated answer for a way to further exploit having X fixed. – Dalesman

setop seems interesting, didn't know it before. Could you elaborate a bit more how it works? – Backstairs

I usually use it to operate on rows of a matrix with a vector with the same length as number of columns. It operates by reference, which makes it fast and memory efficient, but you have to take care if you don't want to overwrite the matrix. See https://mcmap.net/q/262991/-how-to-do-elementwise-multiplication-of-big-matrix-with-vector-very-fast. – Dalesman

Answer 2

I think you should reduce the number of %*% operators used in your calculation pipe, which should be the most straightforward and effective way to save time.

Code Optimization

For example, you can move your terms in the expression like below

exp(X %*% log(pr.t / (1 - pr.t)) + t(colSums(log(1 - pr.t)))[rep.int(1, nrow(X)), ]) %*% wts

where only the %*% operator is used only twice (instead of 3 as in your original scheme)

---

Benchmark

We compare your solution, @jblood94's solution, and my solution and see how the performance looks like

# pre-processing since they keep fixed during iterations
n <- ncol(X)
X0 <- unique(X)
mX0 <- 1 - X0
i <- match(X %*% 2^((n - 1):0), X0 %*% 2^((n - 1):0))

f_dhc <- function(X, pr.t, wts) {
    mX <- 1 - X
    exp(X %*% log(pr.t) + mX %*% log(1 - pr.t)) %*% wts
}

f_jblood94_1 <- function(X, pr.t, wts) {
    (exp(X0 %*% log(pr.t) + mX0 %*% log1p(-pr.t)) %*% wts)[i, , drop = FALSE]
}

f_jblood94_2 <- function(X, pr.t, wts) {
    (exp(X0 %*% log(pr.t / (1 - pr.t)) + t(colSums(log1p(-pr.t)))[rep.int(1, nrow(X0)), ]) %*% wts)[i, , drop = FALSE]
}

f_TIC1 <- function(X, pr.t, wts) {
    exp(X %*% log(pr.t / (1 - pr.t)) + t(colSums(log(1 - pr.t)))[rep.int(1, nrow(X)), ]) %*% wts
}

f_TIC2 <- function(X, pr.t, wts) {
    exp(X %*% log(pr.t / (1 - pr.t)) + outer(rep.int(1, nrow(X)), colSums(log(1 - pr.t)))) %*% wts
}

f_TIC3 <- function(X, pr.t, wts) {
    exp(X %*% log(pr.t / (1 - pr.t)) + kronecker(matrix(rep.int(1, nrow(X))), t(colSums(log(1 - pr.t))))) %*% wts
}

f_TIC4 <- function(X, pr.t, wts) {
    exp(X %*% qlogis(pr.t) + t(colSums(log1p(-pr.t)))[rep.int(1, nrow(X)), ]) %*% wts
}

mbm <- microbenchmark(
    dhc = f_dhc(X, pr.t, wts),
    jblood94_1 = f_jblood94_1(X, pr.t, wts),
    jblood94_2 = f_jblood94_2(X, pr.t, wts),
    TIC1 = f_TIC1(X, pr.t, wts),
    TIC2 = f_TIC2(X, pr.t, wts),
    TIC3 = f_TIC3(X, pr.t, wts),
    TIC4 = f_TIC4(X, pr.t, wts),
    check = "equal",
    unit = "relative"
)

• Small-size data

set.seed(0)
p <- 1000
q <- 5
r <- 15
X <- matrix(sample(c(0, 1), p * q, replace = TRUE), p, q)
pr.t <- matrix(runif(r * q), q, r)
wts <- runif(r)

and we will see

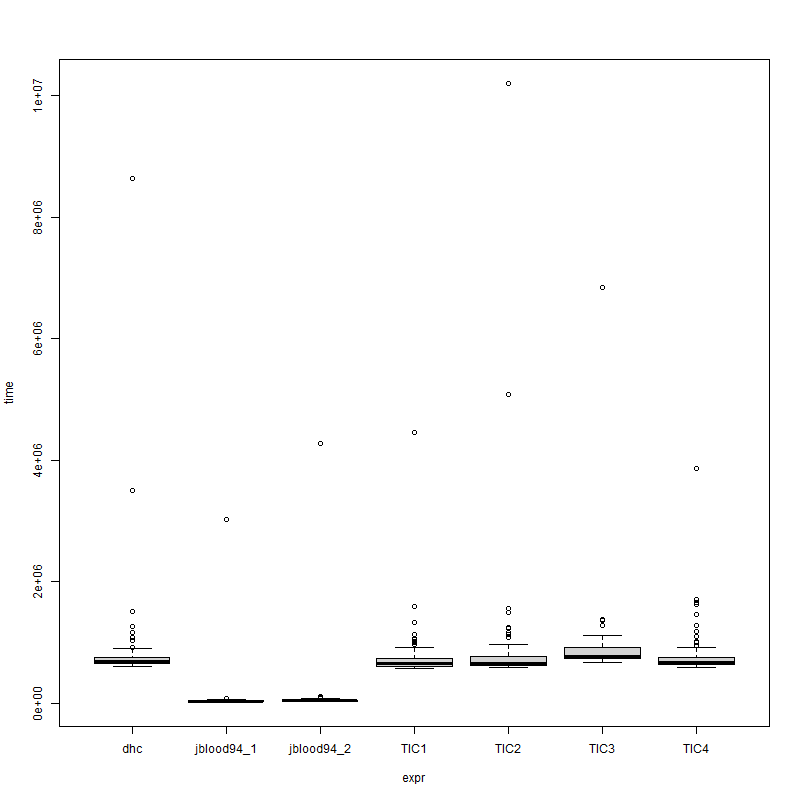
> mbm
Unit: relative
       expr       min        lq     mean    median        uq       max neval
        dhc 22.869560 22.049715 19.49625 19.354935 17.437032 20.113939   100
 jblood94_1  1.000000  1.000000  1.00000  1.000000  1.000000  1.000000   100
 jblood94_2  1.255509  1.448805  1.59287  1.521874  1.652512  1.655629   100
       TIC1 22.380653 20.909609 10.14739 18.157829 17.205723  1.243090   100
       TIC2 22.621384 21.141098 11.76505 18.266085 17.322903  3.590901   100
       TIC3 26.265694 25.490583 12.36498 22.410242 19.683481  1.743739   100
       TIC4 22.921410 21.263929 10.45764 19.084340 17.894608  1.141133   100

and plot(mbm) shows

• Big-size data

set.seed(0)
p <- 1000
q <- 1000
r <- 100
X <- matrix(sample(c(0, 1), p * q, replace = TRUE), p, q)
pr.t <- matrix(runif(r * q), q, r)
wts <- runif(r)

and we will see

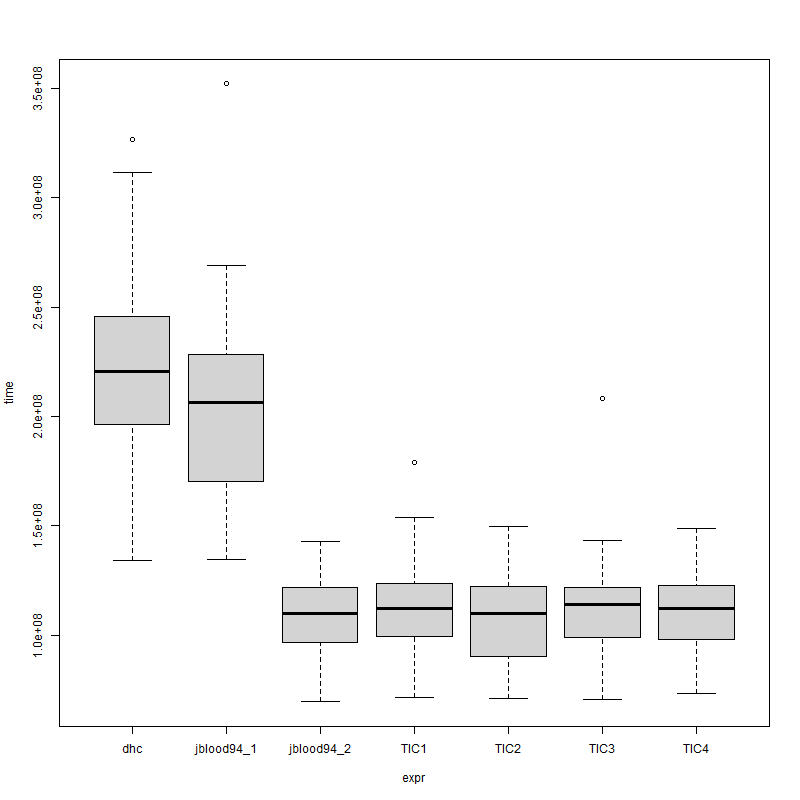
> mbm
Unit: relative
       expr       min       lq     mean   median        uq       max neval
        dhc 1.8862821 2.172686 2.030361 2.005938 2.0100325 2.1832300   100
 jblood94_1 1.8933325 1.884341 1.881695 1.875507 1.8684887 2.3552021   100
 jblood94_2 0.9776827 1.071931 1.016522 1.000148 0.9974477 0.9546140   100
       TIC1 1.0086822 1.099217 1.035331 1.018304 1.0093273 1.1968782   100
       TIC2 1.0000000 1.000000 1.000000 1.000000 1.0000000 1.0000000   100
       TIC3 0.9939343 1.095266 1.038841 1.037027 0.9967151 1.3936333   100
       TIC4 1.0297307 1.084197 1.024587 1.018200 1.0050159 0.9950423   100

and plot(mbm) shows

Backstairs

Calculation of i should not be included in the benchmark since it will be calculated only once, while the matrix multiplication is repeated over many iterations. But, really the better solution would be to combine the brilliantly reformulated matrix multiplication you propose with the size reduction provided by my answer. – Dalesman

@thomasIsCoding, your example is clearly fast. But, if I change the dimensions of p <- 1000; q <- 5; r <- 15 and run the code I get Error: Input expressions are not equivalent.. I'm staring at the code to find why now, but this is stumping me, perhaps you see why. – Petrography

@Petrography Sorry that I had a typo in f_TIC1, and it should be t(colSums(log(1 - pr.t)))[rep.int(1, nrow(X)), ] – Backstairs

For the "big-size data", the size reduction is based on the premise that nrow(X) is much larger than nrow(unique(X)). That condition goes away when the number of columns of X grows. The size of the actual data becomes very important. – Dalesman

@Dalesman yes, I see that point as well. Your approach takes full advantage of nrow(unique(X)). I built a function f_jblood94_2 to combine both yours and mine, and you can see the performance. – Backstairs

Consider also qlogis(p) which is log(p/(1-p)). – Oof

@MikaelJagan Thanks for the advice, looks more concise, but seems no big speed improvement. – Backstairs

Try (setop(exp(X0 %*% qlogis(pr.t)), "*", colprods(1 - pr.t), rowwise = TRUE) %*% wts)[i, , drop = FALSE] with the Rfast and collapse packages. – Dalesman