How to find the greatest possible euclidean distance we can achieve by moving using given set of vectors

Question

That's a problem from Polish Olympiad in Informatics, called Pionek (PIO).

Given a set of not unique vectors, find the greatest possible euclidean distance in reference to (0,0) point you can achieve by moving using vectors from the set. Every vector can be used only once. Return square of found distance.

1. For every vector [x, y] from set, we know that 10^-4 <= x,y <= 10^4

2. For n, number of vectors in set, the inequality n <= 200 000 is satisfied

3. Memory limit is 128MB

Example input:

5 -> number of vectors
2 -2 -> [x, y] vector
-2 -2
0 2
3 1
-3 1

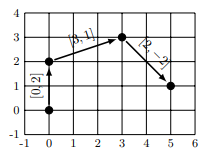
We will achieve the best result by choosing vectors [0,2], [3,1], [2, -2]. Our final destination point will be (5, 1), so the square of euclidean distance from (0,0) to (5,1) is 26, and that's valid result for this input.

I wrote below brute force solution:

#include <iostream>
#include <vector>

using namespace std;

long long solve(const vector<pair<int, int>>& points, int i, int x, int y) {
    if (i == points.size())
        return 1LL * x * x + 1LL * y * y;

    long long ans = 0;
    ans = max(solve(points, i + 1, x, y), solve(points, i + 1, x + points[i].first, y + points[i].second));
    return ans;
}

int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n;
    cin >> n;

    vector<pair<int, int>> points(n);
    for (int i = 0; i < n; ++i)
        cin >> points[i].first >> points[i].second;

    cout << solve(points, 0, 0, 0);
}

Of course, it's too slow (most of test cases require execution time below 0.5s or below 1.5s). I can use memoization, but then I exceed the memory limit.

Except above brute force, I have no idea what could I do. How can we solve it with acceptable time complexity, like O(nlogn)?

Martyrology

Sort first?!!!? – Anecdote

It would help if you described what you mean with "brute force", because that's sometimes not totally clear. – Breccia

@UlrichEckhardt The brute force solution provided here is just trying all subsets of the vectors. – Vowell

Compare the brute force solution to the sum of all vectors. (I expect it to be in the same half space.) – Loose

@AhmedAEK This problem was from a contest (so it is certainly solvable) and there is a clear O(N log N) solution. – Vowell

Note that, though perhaps obvious, for any collection of vectors, the end point is the same for all orderings of those vectors. – Galingale

Answer 1

There is one simple approach that should allow you to simplify the algorithm. The idea is that you decide for a final direction first and then discard everything that doesn't provide a net benefit.

In more detail:

1. You sort all vectors so that they increase in angle. atan2() helps you there.
2. You take the first vector and then add all following vectors until the net result decreases in length. The vectors you selected then will sweep an angle of up to 180 degrees. If this partial result is better than the one before, you store the indices as result.
3. Rotate the sequence of vectors, so that the first one is last and the second one comes first.
4. Repeat step 2 until you fully rotated through all vectors.

This of course isn't optimal yet. In order to improve it, you don't rotate the vectors (lots of copying required) but just access them in a circular way (apply modulo operator to the index). Further, you use a sliding window over the vectors. That means that once you reached the optimal end vector for a certain start vector (to get one result), you delete the start vector from the sum for the next round. This avoids having to add up all vectors by which two windows overlap.

BTW: If implemented with the two additional hacks, this should run in O(n log n) time and O(1) space. Rationale for the time: First, sorting can be done in O(n log n). Then, for the first window, you add on average O(n/2) vectors. Then, for each of the other n-1 windows, every vector will get added once and get deleted once (O(1) on average), making it O(n). Rationale for the space: You only keep the best result using one vector and the two indices for the window.

Breccia