Obtain first significant digits of a number using variable-precision arithmetic

Question

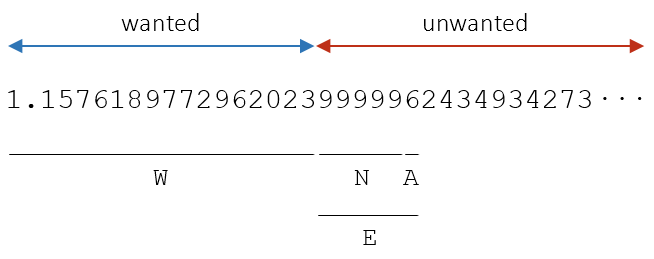
Assume you want to know the first W significant digits of a number, say pi, using vpa. Simply calling vpa with that many digits does not work. Consider the following example with W = 35:

>> disp(vpa(sym('pi'), 35))
3.1415926535897932384626433832795029

The reason why this doesn't work is rounding. Specifically, the above result appears to indicate that the 35-th significant digit of pi is nine, when actually it is an eight that was rounded up:

>> disp(vpa(sym('pi'), 36))
3.14159265358979323846264338327950288

---

From the above, it would appear that a solution is to ask for one extra decimal and throw it away, so that the last surviving decimal doesn't have rounding issues. But this does not work in general either, because rounding can cause carry. See this example in Matlab:

>> disp(vpa(sym('pi'), 79))
3.141592653589793238462643383279502884197169399375105820974944592307816406286209
>> disp(vpa(sym('pi'), 80))
3.141592653589793238462643383279502884197169399375105820974944592307816406286209
>> disp(vpa(sym('pi'), 81))
3.141592653589793238462643383279502884197169399375105820974944592307816406286209
>> disp(vpa(sym('pi'), 82))
3.141592653589793238462643383279502884197169399375105820974944592307816406286208999
>> disp(vpa(sym('pi'), 83))
3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986

or in Octave:

>> disp(vpa(sym('pi'), 79))
3.141592653589793238462643383279502884197169399375105820974944592307816406286209
>> disp(vpa(sym('pi'), 80))
3.1415926535897932384626433832795028841971693993751058209749445923078164062862090
>> disp(vpa(sym('pi'), 81))
3.14159265358979323846264338327950288419716939937510582097494459230781640628620900
>> disp(vpa(sym('pi'), 82))
3.141592653589793238462643383279502884197169399375105820974944592307816406286208999
>> disp(vpa(sym('pi'), 83))
3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986

As can be seen,

• Increasing the number of required decimals from 79 to 80 or 81 in vpa gives the same answer in Matlab, because rounding and carry make the last digits zero and Matlab trims trailing zeros.
• Octave doesn't trim, so it shows those zeros, but they are still incorrect.

Thus, both in Matlab and in Octave, correctly obtaining the first 79 significant digits requires that at least three extra digits be asked for in this case.

---

The above examples illustrate that

• The last digits of vpa may be off because of rounding;
• It doesn't always suffice to ask for one extra digit;
• The number of extra digits required to avoid rounding issues can be arbitrarily large. This happens when there is a long run of nines right after the wanted digits.

So, is there a way to obtain the first W significant digits of a number with guarantee that they are correct, i.e not affected by rounding issues?

Skill

Answer 1

First off, it doesn't seem possible to predict when vpa will round away or towards zero. The following results are not consistent with "round half away from zero", "round half to even", or any of the usual rules:

>> disp(vpa(sym('0.135'),2))
0.14
>> disp(vpa(sym('0.125'),2))
0.12
>> disp(vpa(sym('0.115'),2))
0.11

Octave's results are also inconsistent, and different from Matlab's:

>> disp(vpa(sym('0.135'),2))
0.14
>> disp(vpa(sym('0.125'),2))
0.13
>> disp(vpa(sym('0.115'),2))
0.11

This impredictability doesn't really affect the answer, but it forces it to be phrased in more generic terms, without assuming any specific rounding rule.

---

Let W be the wanted number of digits. All digits beyond that will be referred to as unwanted. Let N be the (possibly zero) number of initial nines in the unwanted part, and let A = 1 if the first unwanted digit that is not nine causes the preceding digit to be rounded away from zero, and A = 0 otherwise. The figure illustrates this.

From the observations in the question, there are four possible cases. In the following examples the number of wanted digits is W = 3, and Matlab is used.

1. N = 0, A = 0: no extra digits are required.

   >> disp(vpa(sym('0.12345'),3)) % works: first 3 digits are correct
   0.123
   

2. N = 0, A = 1: one extra digit is required to correctly obtain the first W = 3 digits:

   >> disp(vpa(sym('0.12378'),3)) % doesn't work
   0.124
   >> disp(vpa(sym('0.12378'),4)) % works: first 3 digits are correct
   0.1238
   

3. N > 0, A = 0: N extra digits are required:

   >> disp(vpa(sym('0.123994'),3)) % doesn't work
   0.124
   >> disp(vpa(sym('0.123994'),4)) % doesn't work
   0.124
   >> disp(vpa(sym('0.123994'),5)) % works: first 3 digits are correct
   0.12399
   

4. N > 0, A = 1: N+1 extra digits are required:

   >> disp(vpa(sym('0.123997'),3)) % doesn't work
   0.124
   >> disp(vpa(sym('0.123997'),4)) % doesn't work
   0.124
   >> disp(vpa(sym('0.123997'),5)) % doesn't work
   0.124
   >> disp(vpa(sym('0.123997'),6)) % works: first 3 digits are correct
   0.123997
   

Let E denote the amount of extra digits that need to be asked from vpa to ensure that the first W digits are correct. Then the four cases above can be summarized by the rule E = N + A.

In practice both N and A are unknown. Therefore, a possible approach is to try E = 1 and keep increasing E until the last obtained digit is not a (possibly trimmed) 0. Then, discarding the last E digits gives the desired result. This approach uses E = max(1, N+A); that is, the number of extra digits is the minimum possible except that one extra digit is used when no extra digits are actually required (case 1 above).

The code below implements this for real or imaginary numbers, with output possibly using scientific notation. Complex numbers are not supported (the number of digits is more difficult to find from the output string).

s = sym('pi'); % number in symbolic form
W = 79; % number of wanted digits
E = 0; % initiallize
done = false;
while ~done
    E = E+1;
    x = char(vpa(s, W+E));
    y = regexprep(x, '^[+-]?0*|\.0*', ''); % remove sign, leading zeros,
        % decimal point and zeros right after the point; if present
    y = regexprep(y, '\D.*$', ''); % remove exponent and imaginary unit,
        % if present
    num_digits = numel(y); % get number of significant digits in x: 
    done = num_digits==W+E && x(end)~='0'; % the second condition is only
        % required in Octave, but it doesn't harm to keep it in Matlab too
end
c = find(~ismember(x, ['0':'9' '+-.']), 1);
if c % there is an exponent or/and imaginary unit
    result = [x(1:c-1-E) x(c:end)]; % discard last E digits before
        % exponent or imaginary unit
else
    result = x(1:end-E); % discard last E digits
end

Skill

I believe this only works under the assumption that there are more digits (which of course isn't a problem for e.g. pi) – Brioche

What do you mean by "more digits"? There are always more digits, even if they are all zero :-) For example, using s = sym('1.2'); W = 20; correctly produces result = '1.2000000000000000000' ` – Skill

Yes, I meant after the trailing zeros had been cut off :D. I agree, that it produces the correct results, but only because of numerical inaccuracies. e.g. your example with s = sym('1.2'); only terminates because it encounters a 1 at some point in the expansion. 1.25 have an exact hexadecimal expansion and will thus not terminate – Brioche

Answer 2

The problem occurs because Matlab uses guard digits to increase precision as described by Matlab:

The number of digits that you specify using the vpa function or the digits function is the guaranteed number of digits. Internally, the toolbox can use a few more digits than you specify. These additional digits are called guard digits.

To solve the problem, we have to turn the use of guard digits off. (Un)fortunately, Matlab does not allow the user to specify the number of guard digits, this is something which is "calculated" internally. However, John D'Errico has written a High precision floating point arithmetic class (HPF), where you can specify the number of guard digits yourself.

DefaultNumberOfDigits 100 0
DefaultDecimalBase 1

which will set the default number of digits to 100 with 0 guard digits and store the migits in "tuples" of 1. If we now go back to the Pi example, we get

pie = hpf('pi',79)
pie = 3.141592653589793238462643383279502884197169399375105820974944592307816406286208

pie = hpf('pi',80)
pie = 3.1415926535897932384626433832795028841971693993751058209749445923078164062862089

pie = hpf('pi',81)
pie = 3.14159265358979323846264338327950288419716939937510582097494459230781640628620899

pie = hpf('pi',82)
pie = 3.141592653589793238462643383279502884197169399375105820974944592307816406286208998 

NOTE: This is a solution which solves the rounding problem. There are still the standard problem when you start to use the numbers for calculations. E.g. having the number 5 with 100 digits precision, does not give you sqrt(5) with 100 digits precision. This is basically why we have guard digits, they add precision "without" telling us.

Brioche

I'm not sure I follow. Are you saying that specifying 0 guard digits guarantees that the output digits are correct. i.e. no rounding up? Also, what is a "tuble"? – Skill

If there are no guard digits, then there is nothing to round up. The HPF class represents numbers as a vector of n digit numbers (called migits) where n is DefaultDecimalBase, e.g. 8 digits of 1.2 with n=4 and zero guard digits is represented as [1200, 0000]; thus if you only asked for 7 digits then it would overwright your choice of 0 guard digits and use 1 (to make the total divisible by 4). Thus by putting n=1 it is a bit slower (the migits would be [1,2,0,0,0,0,0,0]), but we have full control over the number of guard digits. – Brioche

As for correctness then it fails, whenever you start to calculate with the numbers, without guard digits the precision deteriorates quickly e.g. having the number 5 with 100 digits will not ensure that you also have 100 digits of sqrt(5) – Brioche

Thanks for the explanation. This doesn't exactly answer my question because HPF is floating-point with a fixed number of significant digits, not variable-precision (symbolic) arithmetic. But it's quite interesting! – Skill

You are welcome. Apparently, my brain chose not to read the "variable-precision" :) – Brioche