Simple Linear Regression using Keras

Question

I have been trying to implement a simple linear regression model using neural networks in Keras in hopes to understand how do we work in Keras library. Unfortunately, I am ending up with a very bad model. Here is the implementation:

from pylab import *
from keras.models import Sequential
from keras.layers import Dense

#Generate dummy data
data = data = linspace(1,2,100).reshape(-1,1)
y = data*5

#Define the model
def baseline_model():
   model = Sequential()
   model.add(Dense(1, activation = 'linear', input_dim = 1))
   model.compile(optimizer = 'rmsprop', loss = 'mean_squared_error', metrics = ['accuracy'])
   return model


#Use the model
regr = baseline_model()
regr.fit(data,y,epochs =200,batch_size = 32)
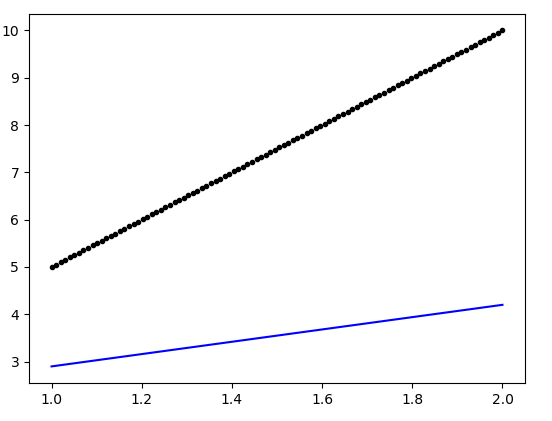
plot(data, regr.predict(data), 'b', data,y, 'k.')

The generated plot is as follows:

Can somebody point out the flaw in the above definition of the model (which could ensure a better fit)?

Arquebus

Answer 1

You should increase the learning rate of optimizer. The default value of learning rate in RMSprop optimizer is set to 0.001, therefore the model takes a few hundred epochs to converge to a final solution (probably you have noticed this yourself that the loss value decreases slowly as shown in the training log). To set the learning rate import optimizers module:

from keras import optimizers

# ...
model.compile(optimizer=optimizers.RMSprop(lr=0.1), loss='mean_squared_error', metrics=['mae'])

Either of 0.01 or 0.1 should work fine. After this modification you may not need to train the model for 200 epochs. Even 5, 10 or 20 epochs may be enough.

Also note that you are performing a regression task (i.e. predicting real numbers) and 'accuracy' as metric is used when you are performing a classification task (i.e. predicting discrete labels like category of an image). Therefore, as you can see above, I have replaced it with mae (i.e. mean absolute error) which is also much more interpretable than the value of loss (i.e. mean squared error) used here.

Vaudois

I have provided an data for which literally a straight line fits perfectly. Hence the expected loss should be 0. But by this computation, the loss is oscillates around 0.015. Is this an inherent problem of the model or it can be perfected to get better values? – Arquebus

@Arquebus It is due to the method of optimization of neural networks, which is gradient based and gradual, and also due to the optimizer used. I guess since your case is a simple one you may get better results using a less sophisticated optimizer such as simple stochastic gradient method, i.e. optimizers.SGD() with a learning rate of lr=0.1. I guess after 200 epochs you would reach a loss of around 1e-4 or 1e-5 by using SGD. But as the optimization process is gradual and step by step, rather than definite, don't expect to reach an exact loss of zero. – Vaudois

Answer 2

The below code best fits for your data.

Take a look at this.

from pylab import *
from keras.models import Sequential
from keras.layers import Dense
import matplotlib.pyplot as plt
%matplotlib inline

​# Generate dummy data

data = data = linspace(1,2,100).reshape(-1,1)
y = data*5

​ # Define the model

def baseline_model():
    global num_neurons
    model = Sequential()
    model.add(Dense(num_neurons, activation = 'linear', input_dim = 1))
    model.add(Dense(1 , activation = 'linear'))
    model.compile(optimizer = 'rmsprop', loss = 'mean_squared_error')
    return model

set num_neurons in first dense layer

** You may change it later

num_neurons = 17

​ ​#Use the model

regr = baseline_model()
regr.fit(data,y,epochs =200, verbose = 0)
plot(data, regr.predict(data), 'bo', data,y, 'k-')

the first plot with num_neurons = 17 , is good fit.

But even we can explore more.

click on the links below to see the plots

Plot for num_neurons = 12

Plot for num_neurons = 17

Plot for num_neurons = 19

Plot for num_neurons = 20

You can see that , as we increase the num of neurons

our model is becoming more intelligent. and best fit.

I hope you got it.

Thank you

Seamus

Im using TF2. This seems to work better for me than the accepted answer. – Brahear

I hope u got it. – Seamus

Answer 3

Interesting problem, so I plugged the dataset into a model-builder framework I wrote. The framework has two callbacks: EarlyStopping callback for 'loss' and Tensorboard for analysis. I removed the 'metric' attribute from the model compile - unnecessary, and should be 'mae' anyways.

@mathnoob123 model as written and learning rate(lr) = 0.01 had a loss=1.2623e-06 in 2968 epochs

BUT the same model replacing the RMSprop optimizer with Adam was most accurate with loss=1.22e-11 in 2387 epochs.

The best compromise I found was @mathnoob123 model using lr=0.01 results in loss=1.5052e-4 in 230 epochs. This is better than @Kunam's model with 20 nodes in the first dense layer with lr=0.001: loss=3.1824e-4 in 226 epochs.

Now I'm going to look at randomizing the label dataset (y) and see what happens....

Brahear