How to implement adaptive step size Runge-Kutta Cash-Karp?

Question

Trying to implement an adaptive step size Runge-Kutta Cash-Karp but failing with this error:

home/anaconda/lib/python3.6/site-packages/ipykernel_launcher.py:15: RuntimeWarning: divide by zero encountered in double_scalars from ipykernel import kernelapp as app

The ODE i am trying to solve (and using in the example below, transformed from higher order to system of 1st order ODEs) is the following:

Here is the implementation I am using:

def rkck(f, x, y, h, tol):
    #xn = x + h
    err = 2 * tol
    while (err > tol):
        xn = x + h
        k1 = h*f(x,y)
        k2 = h*f(x+(1/5)*h,y+((1/5)*k1)) 
        k3 = h*f(x+(3/10)*h,y+((3/40)*k1)+((9/40)*k2))
        k4 = h*f(x+(3/5)*h,y+((3/10)*k1)-((9/10)*k2)+((6/5)*k3))
        k5 = h*f(x+(1/1)*h,y-((11/54)*k1)+((5/2)*k2)-((70/27)*k3)+((35/27)*k4))
        k6 = h*f(x+(7/8)*h,y+((1631/55296)*k1)+((175/512)*k2)+((575/13824)*k3)+((44275/110592)*k4)+((253/4096)*k5))
        yn4 = y + ((37/378)*k1)+((250/621)*k3)+((125/594)*k4)+((512/1771)*k6)
        yn5 = y + ((2825/27648)*k1)+((18575/48384)*k3)+((13525/55296)*k4)+((277/14336)*k5)+((1/4)*k6)
        err = yn4[-1]-yn5[-1]
        if (err != 0):
            h = 0.8 * h * (tol/err)**(1/float(5))
        yn = yn4
    return xn, yn

def integrate_sStepControl(f, t0, y0, tend, h, tol):
    T = [t0]
    Y = [y0]
    t = t0
    y = y0 
    while (t < tend):
        h = min(h, tend-t)
        t, y = rkck(f, t, y, h, tol)
        T.append(t)
        Y.append(y)
    return np.array(T), np.array(Y)

def f_1(t,y): 
    return np.array([ y[1], -y[0]-(y[0])**3 ])

Y0_f1 = np.array([1.0,1.0])


# Execution
h = 0.05
tv, yv = integrate_sStepControl(f=f_1, t0=0.0, y0=Y0_f1, tend=100.0, h=h, tol=1.0E-05)
print("[ %20.15f, %20.15f]"%(yv[-1,0], yv[-1,1]) )
plt.plot(tv, yv)

Getting the error above, but it gets plotted. Don't know what I am doing wrong here :-/

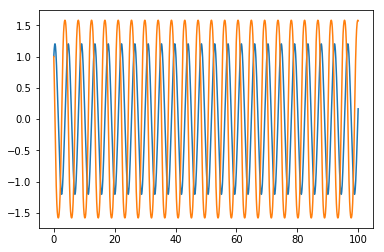
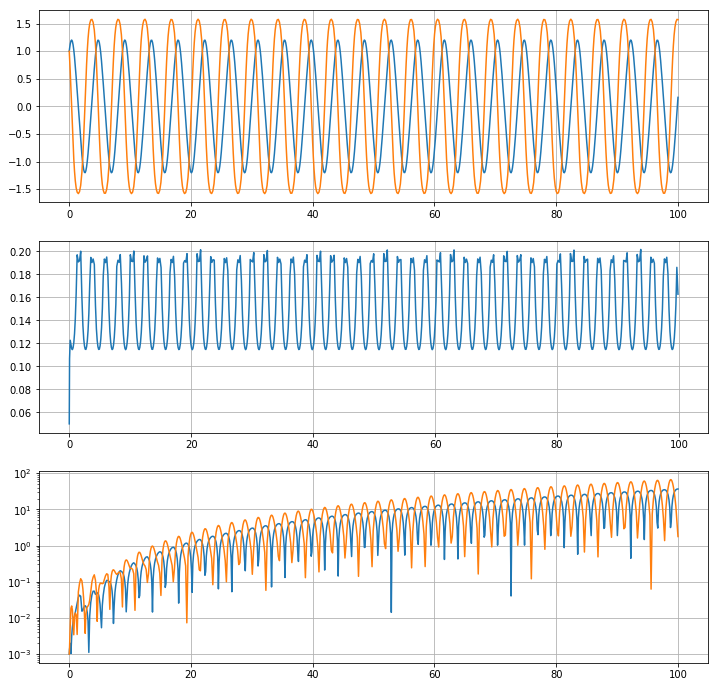
EDIT: Added check for err == 0

Stamina

Done! Thank you! – Stamina

You could put in a check for err == 0 before trying to divide by it. – Microelectronics

Okay. But besides that, what do you think of the implementation? Is it right? – Stamina

If err == 0 then you don't need to calculate h because the while loop will exit and h won't be needed any more. As for the implementation, I don't know, but a good start would be to check the result against a known result. – Microelectronics

You do not pass the computed value of h back to the main loop, so this computation is thrown away. You also need to avoid negative values of err, you can have both by setting err=1e-40+norm(y4-y5). // Please indicate cross-postings of the question to avoid duplicated answers. – Gerick

Answer 1

You need to actually pass back the computed new step size h so that it can be used in the main loop for the first step.

The error should be computed as norm. Add some small number to avoid division by zero.

The leading error term is C*h^5 for the 4th order method. This has to be compared to the desired local error tol*h. In total that results in a 4th root to compute the optimal h. Taking the 5th root provides some kind of dampening, however the effect on the global error is not quite straight-forward.

def rkck(f, x, y, h, tol):
    #xn = x + h
    err = 2 * tol
    while (err > tol):
        xn = x + h
        k1 = h*f(x,y)
        k2 = h*f(x+(1/5)*h,y+((1/5)*k1)) 
        k3 = h*f(x+(3/10)*h,y+((3/40)*k1)+((9/40)*k2))
        k4 = h*f(x+(3/5)*h,y+((3/10)*k1)-((9/10)*k2)+((6/5)*k3))
        k5 = h*f(x+(1/1)*h,y-((11/54)*k1)+((5/2)*k2)-((70/27)*k3)+((35/27)*k4))
        k6 = h*f(x+(7/8)*h,y+((1631/55296)*k1)+((175/512)*k2)+((575/13824)*k3)+((44275/110592)*k4)+((253/4096)*k5))
        dy4 = ((37/378)*k1)+((250/621)*k3)+((125/594)*k4)+((512/1771)*k6)
        dy5 = ((2825/27648)*k1)+((18575/48384)*k3)+((13525/55296)*k4)+((277/14336)*k5)+((1/4)*k6)
        err = 1e-2*tol+max(abs(dy4-dy5))
        # h = 0.95 * h * (tol/err)**(1/5)
        h = 0.8 * h * (tol*h/err)**(1/4)
        yn = y+dy4
    return xn, yn, h

def integrate_sStepControl(f, t0, y0, tend, h, tol):
    T = [t0]
    Y = [y0]
    t = t0
    y = y0 
    while (t < tend):
        h = min(h, tend-t)
        t, y, h = rkck(f, t, y, h, tol)
        T.append(t)
        Y.append(y)
    return np.array(T), np.array(Y)

With that your example gives the following plots for solutions, time steps and error/tol

Gerick

Thank you so much for this answer! Very detailled and couldn't get better! You really helped me understand my error! Don't know how I can thank you more for what you're doing for the scientific community here! – Stamina

According to the en.wikipedia.org/wiki/… chapter about adaptive Runge Kutta, repeating a step if error is too small or too big is mentioned. So, I wonder if your option here is standard or if there is more to the story. – Enure

err = 1e-2*tol+max(abs(dy4-dy5)) What does a 1-ary max function do? – Enure

The case of repeating if the error is too large is realized by the loop in rkck. Using this kind of extremely adapted step size computation rarely leads to a step size that is much too small. Such a lower bound would be needed if one used the older strategy of fixed factors for the increase or decrease of the step size. // Note that if v is a numpy array, then abs(v) is also a numpy array, so that the max is not really unary. – Gerick