Understanding convolutional layers shapes

Question

I've been reading about convolutional nets and I've programmed a few models myself. When I see visual diagrams of other models it shows each layer being smaller and deeper than the last ones. Layers have three dimensions like 256x256x32. What is this third number? I assume the first two numbers are the number of nodes but I don't know what the depth is.

Natatory

Answer 1

TLDR; 256x256x32 refers to the layer's output shape rather than the layer itself.

---

There are many articles and posts out there explaining how convolution layers work. I'll try to answer your question without going into too many details, just focusing on shapes.

Assuming you are working with 2D convolution layers, your input and output will both be three-dimensional. That is, without considering the batch which would correspond to a 4th axis... Therefore, the shape of a convolution layer input will be (c, h, w) (or (h, w, c) depending on the framework) where c is the number of channels, h is the width of the input and w the width. You can see it as a c-channel hxw image. The most intuitive example of such input is the input of the first convolution layer of your convolutional neural network: most likely an image of size hxw with c channels for example c=1 for greyscale or c=3 for RGB...

What's important is that for all pixels of that input, the values on each channel gives additional information on that pixel. Having three channels will give each pixel ('pixel' as in position in the 2D input space) a richer content than having a single. Since each pixel will be encoded with three values (three channels) vs. a single one (one channel). This kind of intuition about what channels represent can be extrapolated to a higher number of channels. As we said an input can have c channels.

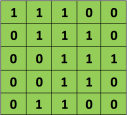
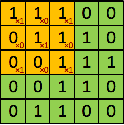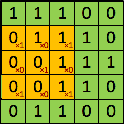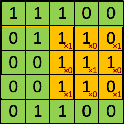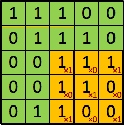
Now going back to convolution layers, here is a good visualization. Imagine having a 5x5 1-channel input. And a convolution layer consisting of a single 3x3 filter (i.e. kernel_size=3)

	input	filter	convolution	output
shape	(1, 5, 5)	(3, 3)		(3,3)
representation

Now keep in mind the dimension of the output will depend on the stride and padding of the convolution layer. Here the shape of the output is the same as the shape of the filter, it does not necessarily have to be! Take an input shape of (1, 5, 5), with the same convolution settings, you would end up with a shape of (4, 4) (which is different from the filter shape (3, 3).

Also, something to note is that if the input had more than one channel: shape (c, h, w), the filter would have to have the same number of channels. Each channel of the input would convolve with each channel of the filter and the results would be averaged into a single 2D feature map. So you would have an intermediate output of (c, 3, 3), which after averaging over the channels, would leave us with (1, 3, 3)=(3, 3). As a result, considering a convolution with a single filter, however many input channels there are, the output will always have a single channel.

From there what you can do is assemble multiple filters on the same layer. This means you define your layer as having k 3x3 filters. So a layer consists k filters. For the computation of the output, the idea is simple: one filter gives a (3, 3) feature map, so k filters will give k (3, 3) feature maps. These maps are then stacked into what will be the channel dimension. Ultimately, you're left with an output shape of... (k, 3, 3).

Let k_h and k_w, be the kernel height and kernel width respectively. And h', w' the height and width of one outputted feature map:

	input	layer	output
shape	(c, h, w)	(k, c, k_h, k_w)	(k, h', w')
description	c-channel hxw feature map	k filters of shape (c, k_h, k_w)	k-channel h'xw' feature map

---

Back to your question:

Layers have 3 dimensions like 256x256x32. What is this third number? I assume the first two numbers are the number of nodes but I don't know what the depth is.

Convolution layers have four dimensions, but one of them is imposed by your input channel count. You can choose the size of your convolution kernel, and the number of filters. This number will determine is the number of channels of the output.

256x256 seems extremely high and you most likely correspond to the output shape of the feature map. On the other hand, 32 would be the number of channels of the output, which... as I tried to explain is the number of filters in that layer. Usually speaking the dimensions represented in visual diagrams for convolution networks correspond to the intermediate output shapes, not the layer shapes.

As an example, take the VGG neural network:

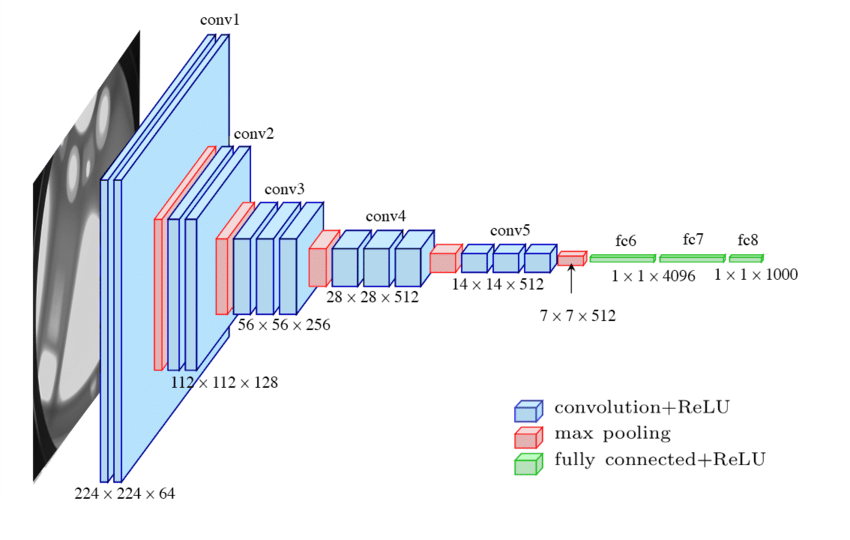_{Very Deep Convolutional Networks for Large-Scale Image Recognition}

Input shape for VGG is (3, 224, 224), knowing that the result of the first convolution has shape (64, 224, 224) you can determine there is a total of 64 filters in that layer.

As it turns out the kernel size in VGG is 3x3. So, here is a question for you: knowing there is a single bias parameter per filter, how many total parameters are in VGG's first convolution layer?

Oho

"256x256 seems extremely high", it looks to me just like the input image size :) Not so high. – Prepuce

OP seemed to have suggested it corresponds to the filter size "Layers have 3 dimensions like 256x256x32". So I was actually referring to a kernel size of 256x256 being extremely high. But of course, it corresponds to a feature map, not a kernel. – Oho

Answer 2

Sorry for the short answer, but when you have a digital image, you have 2 dimensions and then you often have 3 for the colors. The convolutional filter looks into parts of the picture with lower height/width dimensions and much more depth channels (in your case 32) to get more information. This is then fed into the neural network to learn.

Honoria

Answer 3

I created the example in PyTorch to demonstrate the output you had:

import torch
import torch.nn as nn

bs=16
x = torch.randn(bs, 3, 256, 256)
c = nn.Conv2d(3,32,kernel_size=5,stride=1,padding=2)
out = c(x)
print(out.shape, out.shape[1])

Out:

torch.Size([16, 32, 256, 256]) 32

It's a real tensor inside. It may help.

You can play with a lot of convolution parameters.

Prepuce