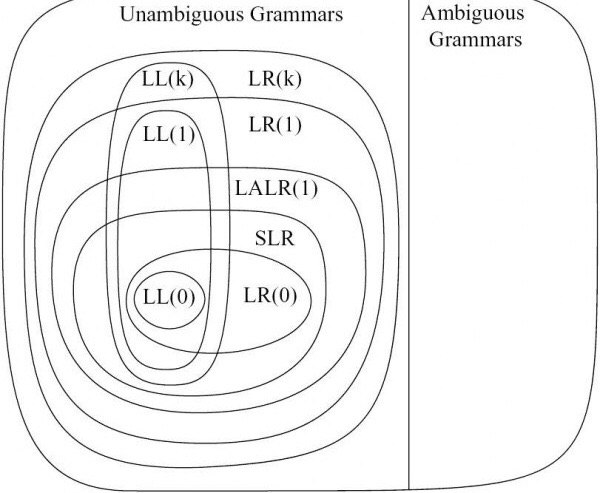
Adding on top of the above answers, the difference in between the individual parsers in the class of bottom-up LR parsers is whether they result in shift/reduce or reduce/reduce conflicts when generating the parsing tables. The less it will have the conflicts, the more powerful will be the grammar (LR(0) < SLR(1) < LALR(1) < CLR(1)).
For example, consider the following expression grammar:
E → E + T
E → T
T → F
T → T * F
F → ( E )
F → id
It's not LR(0) but SLR(1). Using the following code, we can construct the LR0 automaton and build the parsing table (we need to augment the grammar, compute the DFA with closure, compute the action and goto sets):
from copy import deepcopy
import pandas as pd
def update_items(I, C):
if len(I) == 0:
return C
for nt in C:
Int = I.get(nt, [])
for r in C.get(nt, []):
if not r in Int:
Int.append(r)
I[nt] = Int
return I
def compute_action_goto(I, I0, sym, NTs):
#I0 = deepcopy(I0)
I1 = {}
for NT in I:
C = {}
for r in I[NT]:
r = r.copy()
ix = r.index('.')
#if ix == len(r)-1: # reduce step
if ix >= len(r)-1 or r[ix+1] != sym:
continue
r[ix:ix+2] = r[ix:ix+2][::-1] # read the next symbol sym
C = compute_closure(r, I0, NTs)
cnt = C.get(NT, [])
if not r in cnt:
cnt.append(r)
C[NT] = cnt
I1 = update_items(I1, C)
return I1
def construct_LR0_automaton(G, NTs, Ts):
I0 = get_start_state(G, NTs, Ts)
I = deepcopy(I0)
queue = [0]
states2items = {0: I}
items2states = {str(to_str(I)):0}
parse_table = {}
cur = 0
while len(queue) > 0:
id = queue.pop(0)
I = states[id]
# compute goto set for non-terminals
for NT in NTs:
I1 = compute_action_goto(I, I0, NT, NTs)
if len(I1) > 0:
state = str(to_str(I1))
if not state in statess:
cur += 1
queue.append(cur)
states2items[cur] = I1
items2states[state] = cur
parse_table[id, NT] = cur
else:
parse_table[id, NT] = items2states[state]
# compute actions for terminals similarly
# ... ... ...
return states2items, items2states, parse_table
states, statess, parse_table = construct_LR0_automaton(G, NTs, Ts)
where the grammar G, non-terminal and terminal symbols are defined as below
G = {}
NTs = ['E', 'T', 'F']
Ts = {'+', '*', '(', ')', 'id'}
G['E'] = [['E', '+', 'T'], ['T']]
G['T'] = [['T', '*', 'F'], ['F']]
G['F'] = [['(', 'E', ')'], ['id']]
Here are few more useful function I implemented along with the above ones for LR(0) parsing table generation:
def augment(G, S): # start symbol S
G[S + '1'] = [[S, '$']]
NTs.append(S + '1')
return G, NTs
def compute_closure(r, G, NTs):
S = {}
queue = [r]
seen = []
while len(queue) > 0:
r = queue.pop(0)
seen.append(r)
ix = r.index('.') + 1
if ix < len(r) and r[ix] in NTs:
S[r[ix]] = G[r[ix]]
for rr in G[r[ix]]:
if not rr in seen:
queue.append(rr)
return S
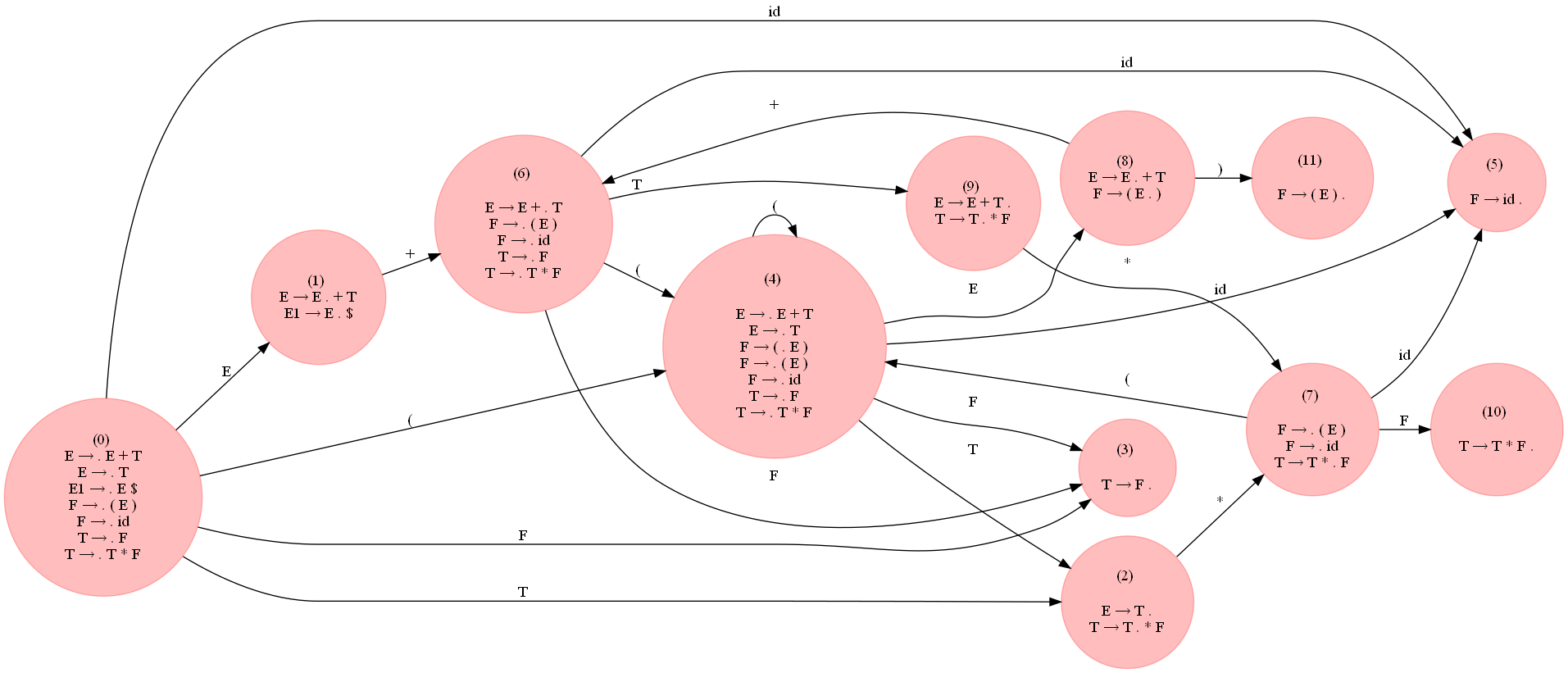
The following figure (expand it to view) shows the LR0 DFA constructed for the grammar using the above code:
![enter image description here]()
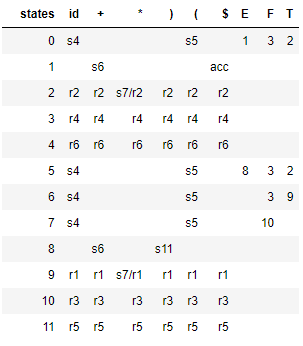
The following table shows the LR(0) parsing table generated as a pandas dataframe, notice that there are couple of shift/reduce conflicts, indicating that the grammar is not LR(0).
![enter image description here]()
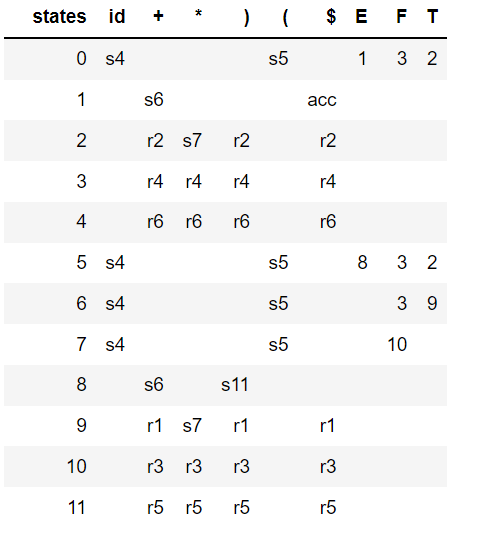
SLR(1) parser avoids the above shift / reduce conflicts by reducing only if the next input token is a member of the Follow Set of the nonterminal being reduced. The following parse table is generated by SLR:
![enter image description here]()
The following animation shows how an input expression is parsed by the above SLR(1) grammar:
![enter image description here]()
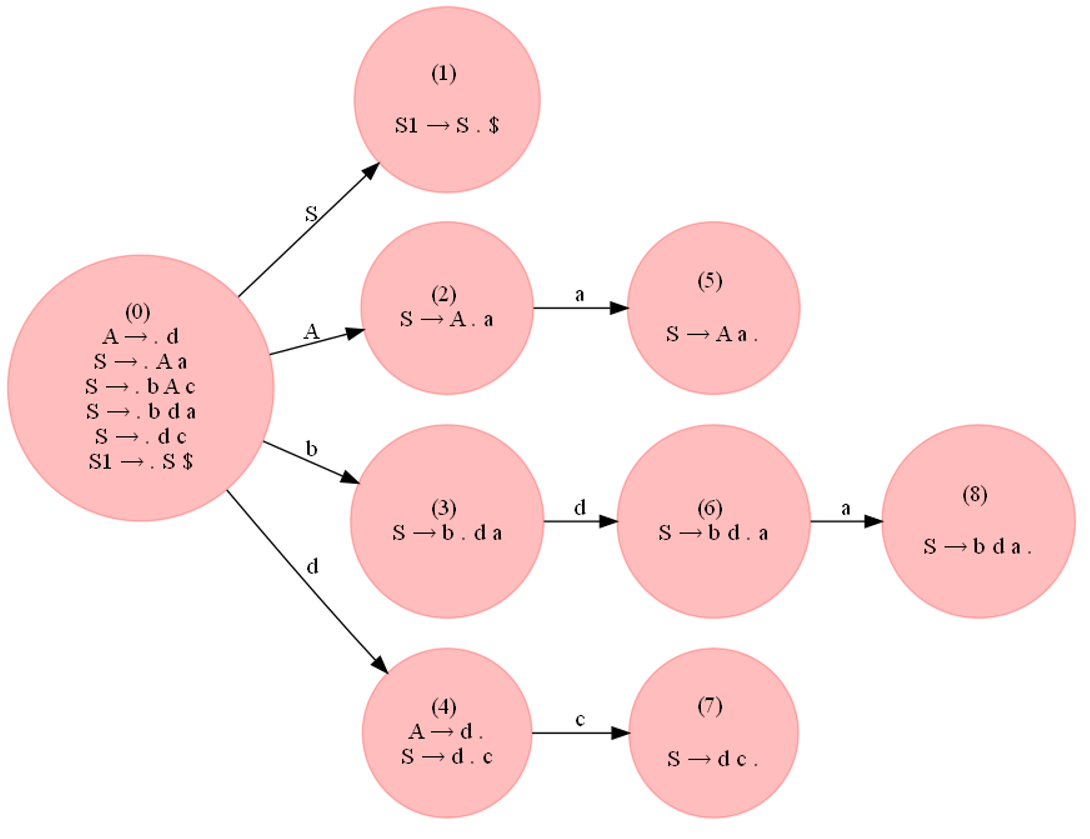
The grammar from the question is not LR(0) as well:
#S --> Aa | bAc | dc | bda
#A --> d
G = {}
NTs = ['S', 'A']
Ts = {'a', 'b', 'c', 'd'}
G['S'] = [['A', 'a'], ['b', 'A', 'c'], ['d', 'c'], ['b', 'd', 'a']]
G['A'] = [['d']]
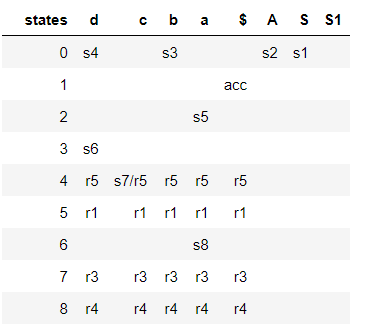
as can be seen from the next LR0 DFA and the parsing table:
![enter image description here]()
there is a shift / reduce conflict again:
![enter image description here]()
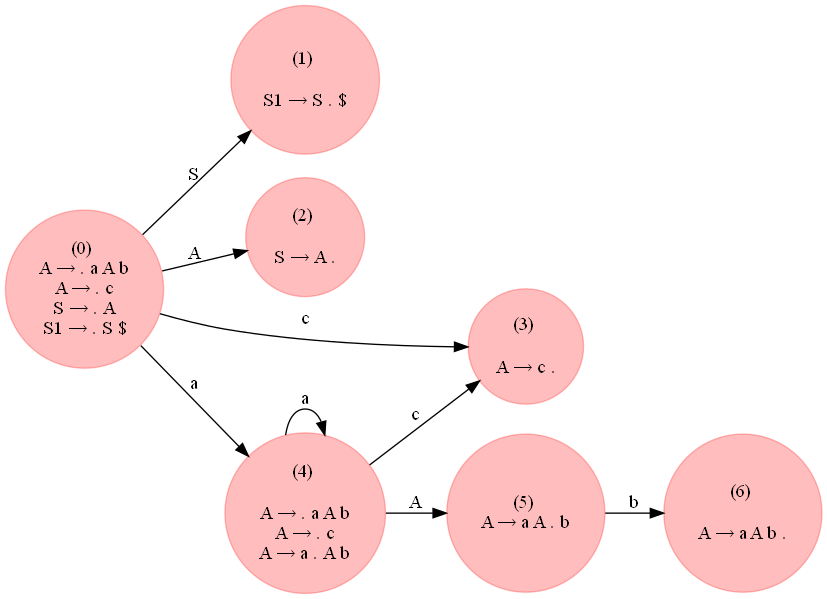
But, the following grammar which accepts the strings of the form a^ncb^n, n >= 1 is LR(0):
A → a A b
A → c
S → A
# S --> A
# A --> a A b | c
G = {}
NTs = ['S', 'A']
Ts = {'a', 'b', 'c'}
G['S'] = [['A']]
G['A'] = [['a', 'A', 'b'], ['c']]
![enter image description here]()
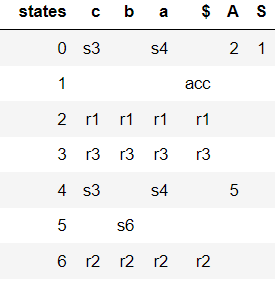
As can be seen from the following figure, there is no conflict in the parsing table generated.
![enter image description here]()
Here is how the input string a^2cb^2 can be parsed using the above LR(0) parse table, using the following code:
def parse(input, parse_table, rules):
input = 'aaacbbb$'
stack = [0]
df = pd.DataFrame(columns=['stack', 'input', 'action'])
i, accepted = 0, False
while i < len(input):
state = stack[-1]
char = input[i]
action = parse_table.loc[parse_table.states == state, char].values[0]
if action[0] == 's': # shift
stack.append(char)
stack.append(int(action[-1]))
i += 1
elif action[0] == 'r': # reduce
r = rules[int(action[-1])]
l, r = r['l'], r['r']
char = ''
for j in range(2*len(r)):
s = stack.pop()
if type(s) != int:
char = s + char
if char == r:
goto = parse_table.loc[parse_table.states == stack[-1], l].values[0]
stack.append(l)
stack.append(int(goto[-1]))
elif action == 'acc': # accept
accepted = True
df2 = {'stack': ''.join(map(str, stack)), 'input': input[i:], 'action': action}
df = df.append(df2, ignore_index = True)
if accepted:
break
return df
parse(input, parse_table, rules)
The next animation shows how the input string a^2cb^2 is parsed with LR(0) parser using the above code:
![enter image description here]()