How i get the PreOrder,InOrder,PostOrder to work?
Here are my current code and implementation, see InOrder(),PreOrder(),PostOrder(). I have a reference from Geek4Geek (https://www.geeksforgeeks.org/tree-traversals-inorder-preorder-and-postorder/).
When i do a print(bst.InOrder()) it return None?
import os
import pygraphviz as pgv
from collections import deque
from IPython.display import Image, display
class BST:
root=None
def get(self,key):
p = self.root
while p is not None:
if p.key == key:
return p.val
elif p.key > key: #if the key is smaller than current node, then go left (since left are all the small ones)
p = p.left
else: # else if key is bigger than current node, go to right (since right are all the big ones)
p = p.right
return None
def put(self, key, val):
self.root = self.put2(self.root, key, val)
def put2(self, node, key, val):
if node is None:
#key is not in tree, create node and return node to parent
return Node(key, val)
if key < node.key:
# key is in left subtree
node.left = self.put2(node.left, key, val)
elif key > node.key:
# key is in right subtree
node.right = self.put2(node.right, key, val)
else:
node.val = val
return node
# draw the graph
def drawTree(self, filename):
# create an empty undirected graph
G=pgv.AGraph('graph myGraph {}')
# create queue for breadth first search
q = deque([self.root])
# breadth first search traversal of the tree
while len(q) != 0:
node = q.popleft()
G.add_node(node, label=node.key+":"+str(node.val))
if node.left is not None:
# draw the left node and edge
G.add_node(node.left, label=node.left.key+":"+str(node.left.val))
G.add_edge(node, node.left)
q.append(node.left)
if node.right is not None:
# draw the right node and edge
G.add_node(node.right, label=node.right.key+":"+str(node.right.val))
G.add_edge(node, node.right)
q.append(node.right)
# render graph into PNG file
G.draw(filename,prog='dot')
display(Image(filename))
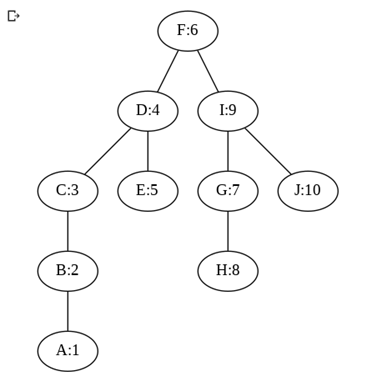
def createTree(self):
self.put("F",6)
self.put('I',9)
self.put("J",10)
self.put("G",7)
self.put("H",8)
# left side of F:6
self.put("D",4)
self.put("C",3)
self.put("B",2)
self.put("A",1)
self.put("E",5)
def createBalancedTree(self):
self.put("F",6)
self.put("A",1)
self.put("B",2)
self.put("C",3)
self.put("D",4)
self.put("E",5)
self.put("G",7)
self.put("H",8)
self.put('I',9)
self.put("J",10)
def find(self, key):
p = self.root
while p is not None:
if p.key == key:
return p
elif p.key > key:
p = p.left
else:
p = p.right
return
def size(self,key):
return self.size2(self.find(key)) #using the find function which gives the node instead
def size2(self, subtree):
if not subtree: #if given key is not found in entire tree (means not a node in this tree)
return 0
else:
return 1 + self.size2(subtree.left) + self.size2(subtree.right)
def depth(self,key):
p = self.root # set the default node as Root, since we start from Root then top-bottom approach.
if p is not None:
if p.key == key: # if key is root, then return 0 (cus at Root, there is no depth)
return 0
elif p.key > key: # if Key is smaller than current node, then search in the left side
return self.depth2(p.left,key,0)
else: # if key is bigger than current node, search the right side
return self.depth2(p.right,key,0)
def depth2(self,node,key,counter):
# lets say you put a depth(Z), at depth(), it wouldt know Z exits or not, so it will call depth2() to find out. In depth2(), It will check 'Z' throughtout node.key>key and node.key<key..
# still cannot find after all the iteration, then it will return None
if node is not None:
if node.key > key:
return self.depth2(node.left,key,counter+1)
elif node.key < key:
return self.depth2(node.right,key,counter+1)
elif node.key == key:
return counter + 1 # this code will only run when you find your key. So example you do depth(E), it will start from F, then D, then found E. In total 2
else:
return None
def height(self,key):
x = self.root
if x == key:
return 0
else:
return self.height2(self.find(key))
def height2(self,subtree):
if not subtree:
return -1 #Key is not a node in the tree
else:
return max(self.height2(subtree.left), self.height2(subtree.right)) + 1
def InOrder(self):
if self == self.root:
InOrder(self.left)
print(self.key)
InOrder(self.right)
#def PreOrder(self):
#def PostOrder(self):
class Node:
left = None
right = None
key = 0
val = 0
def __init__(self, key, val):
self.key = key
self.val = val
What should I do get the print to work?

sizemethod ignores its argument. It does always exactly the same. When called recursively, how could it stop? – Luster