What's the best way to find lines on a very poor quality image, knowing the angle of these lines?

Question

i'm trying to find theses two horizontal lines with the Houghlines transform. As you can see, the picture is very noisy ! Currently my workflow looks like this :

• crop the image

• blur it

• low the noise (for that, I invert the image, and then substract the blured image to the inverted one)

• open it and dilate it with an "horizontal kernel" (kernel_1 = np.ones((10,1), np.uint8)

• threshold

• Houglines

the results are not as good as expected... is there a better strategy, knowing that I will always serach for horizontal lines (hence, abs(theta) will always be closed to 0 or pi)

Montemontefiascone

Answer 1

the issue is the noise and the faint signal. you can subdue the noise with averaging/integration, while maintaining the signal because it's replicated along a dimension (signal is a line).

your approach using a very wide but narrow kernel can be extended to simply integrating along the whole image.

1. rotate the image so the suspected line is aligned with an axis (let's say horizontal)
2. sum up all pixels of one scanline (horizontal line), np.sum(axis=1) or mean, either way mind the data type. working with floats is convenient.
3. work with the 1-dimensional series of values.

this will not tell you how long the line is, only that it's there and potentially spanning the whole width.

edit: since my answer got a reaction, I'll elaborate as well:

I think you can lowpass that to get the "gray" baseline, then subtract ("difference of gaussians"). that should give you a nice signal.

import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
import scipy.ndimage

im = cv.imread("0gczo.png", cv.IMREAD_GRAYSCALE) / np.float32(255)
relief = im.mean(axis=1)
smoothed = scipy.ndimage.gaussian_filter(relief, sigma=2.0)
baseline = scipy.ndimage.gaussian_filter(relief, sigma=10.0)
difference = smoothed - baseline
std = np.std(difference)
level = 2
outliers = (difference <= std * -level)
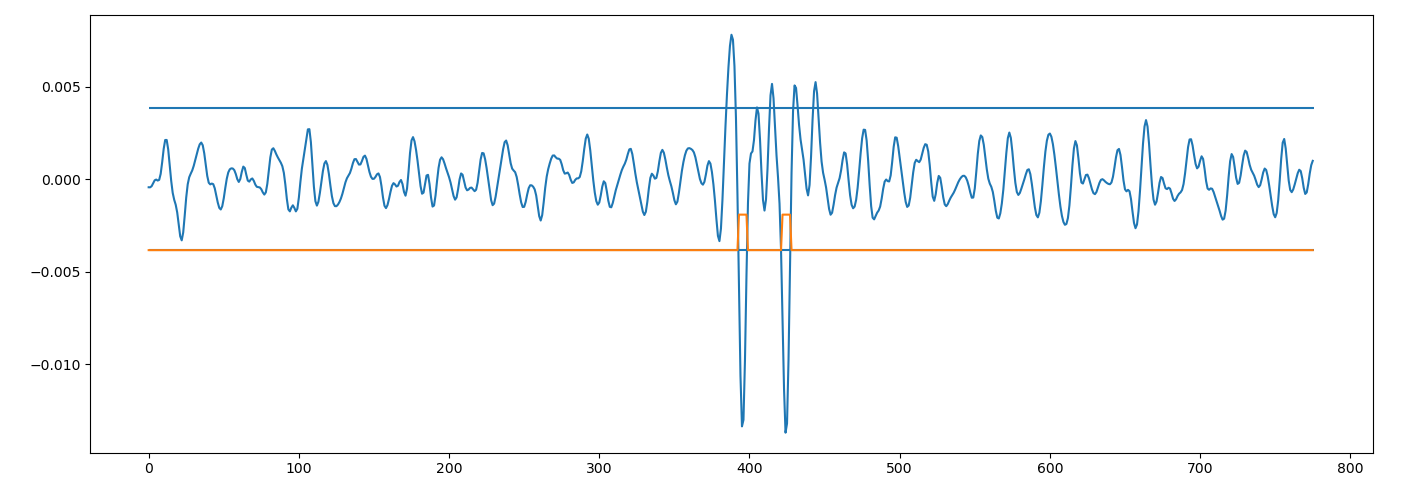
plt.plot(difference)
plt.hlines([std * +level, std * -level], xmin=0, xmax=len(relief))
plt.plot(std * -level + outliers * std)
plt.show()
# where those peaks are:
edgemap = np.diff(outliers.astype(np.int8))
(edges,) = edgemap.nonzero()
print(edges)           # [392 398 421 427]
print(edgemap[edges])  # [ 1 -1  1 -1]

Recapitulation

Sometimes, the simplest solution is the hardest to find, thanks a lot ahahah – Montemontefiascone

Answer 2

Much the same as Christoph's answer, but just wanted to share a processed image which I can't do in the comments.

I just took the mean across the rows with np.mean(axis=1) and normalised the result. Hopefully you can see the two dark bands corresponding to your lines.

Punt