Why does numpy.dot behave in this way?

Question

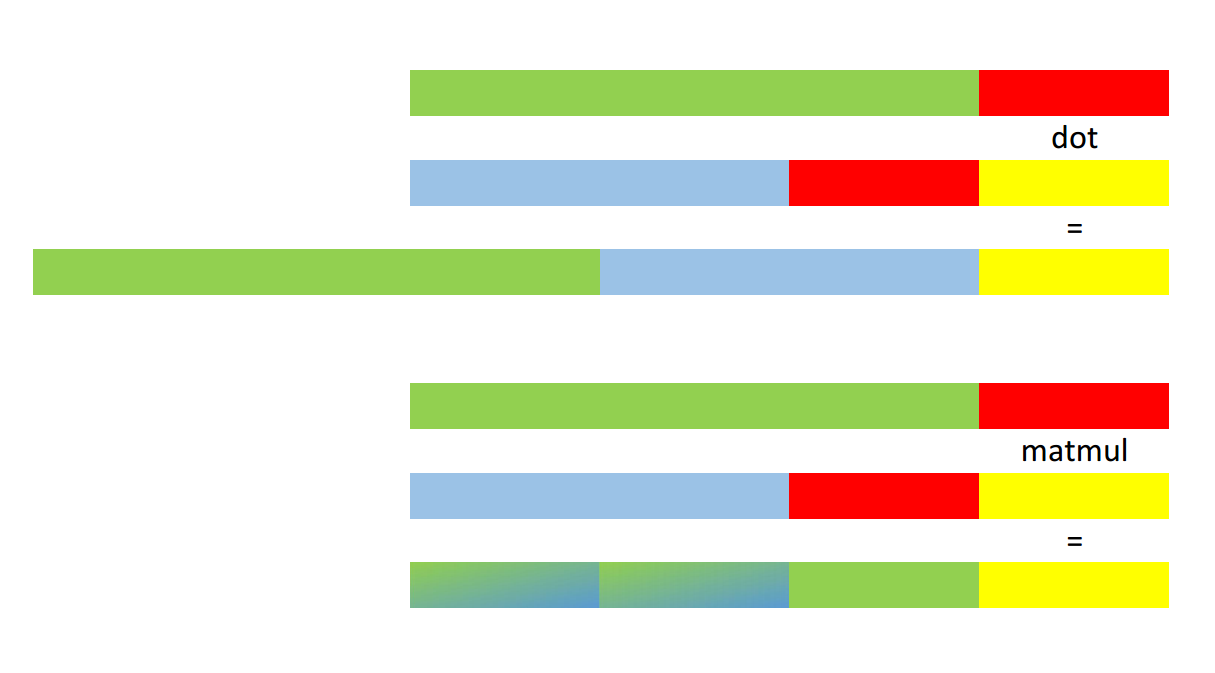
I'm trying to understand why numpy's dot function behaves as it does:

M = np.ones((9, 9))
V1 = np.ones((9,))
V2 = np.ones((9, 5))
V3 = np.ones((2, 9, 5))
V4 = np.ones((3, 2, 9, 5))

Now np.dot(M, V1) and np.dot(M, V2) behave as expected. But for V3 and V4 the result surprises me:

>>> np.dot(M, V3).shape
(9, 2, 5)
>>> np.dot(M, V4).shape
(9, 3, 2, 5)

I expected (2, 9, 5) and (3, 2, 9, 5) respectively. On the other hand, np.matmul does what I expect: the matrix multiply is broadcast over the first N - 2 dimensions of the second argument and the result has the same shape:

>>> np.matmul(M, V3).shape
(2, 9, 5)
>>> np.matmul(M, V4).shape
(3, 2, 9, 5)

So my question is this: what is the rationale for np.dot behaving as it does? Does it serve some particular purpose, or is it the result of applying some general rule?

Shanitashank

this is actually explained in the numpy docs for dot and matmul – Rodrigorodrigue

Answer 1

From the docs for np.dot:

For 2-D arrays it is equivalent to matrix multiplication, and for 1-D arrays to inner product of vectors (without complex conjugation). For N dimensions it is a sum product over the last axis of a and the second-to-last of b:

dot(a, b)[i,j,k,m] = sum(a[i,j,:] * b[k,:,m])

For np.dot(M, V3),

(9, 9), (2, 9, 5) --> (9, 2, 5)

For np.dot(M, V4),

(9, 9), (3, 2, 9, 5) --> (9, 3, 2, 5)

The strike-through represents dimensions that are summed over, and are therefore not present in the result.

---

In contrast, np.matmul treats N-dimensional arrays as 'stacks' of 2D matrices:

The behavior depends on the arguments in the following way.

• If both arguments are 2-D they are multiplied like conventional matrices.
• If either argument is N-D, N > 2, it is treated as a stack of matrices residing in the last two indexes and broadcast accordingly.

The same reductions are performed in both cases, but the order of the axes is different. np.matmul essentially does the equivalent of:

for ii in range(V3.shape[0]):
    out1[ii, :, :] = np.dot(M[:, :], V3[ii, :, :])

and

for ii in range(V4.shape[0]):
    for jj in range(V4.shape[1]):
        out2[ii, jj, :, :] = np.dot(M[:, :], V4[ii, jj, :, :])

Phuongphycology

Here is another example: a1 = np.random.rand(3,4); a2 = np.random.rand(10, 4, 1); A = (a1 @ a2); B = np.array([a1 @ a2[i,:,0] for i in range(10)]); assert A.shape == B.shape; assert np.allclose(A.squeeze(), B) – Brisling

Answer 2

From the documentation of numpy.matmul:

matmul differs from dot in two important ways.

• Multiplication by scalars is not allowed.
• Stacks of matrices are broadcast together as if the matrices were elements.

In conclusion, this is the standard matrix-matrix multiplication you would expect.

On the other hand, numpy.dot is only equivalent to the matrix-matrix multiplication for two-dimensional arrays. For larger dimensions, ...

it is a sum product over the last axis of a and the second-to-last of b:

dot(a, b)[i,j,k,m] = sum(a[i,j,:] * b[k,:,m])

[source: documentation of numpy.dot]

This resembles the inner (dot) product. In case of vectors, numpy.dot returns the dot product. Arrays are considered collections of vectors, and the dot product of them is returned.

Fess

Answer 3

For the why :

dot and matmult are both generalizations of 2D*2D matrix multiplication. But they are a lot of possible choices, according to mathematics properties, broadcasting rules, ...

The choices are for dot and matmul are very different:

For dot, some dimensions (green here) are dedicated to the first array , others (blue) for the second.

matmul need an alignement of stacks regarding to broadcasting rules.

Numpy is born in an image analysis context, and dot can manage easily some tasks by a out=dot(image(s),transformation(s)) way. (see the dot docs in early version of numpy book, p92).

As an illustration :

from pylab import *
image=imread('stackoverflow.png')

identity=eye(3)
NB=ones((3,3))/3
swap_rg=identity[[1,0,2]]
randoms=[rand(3,3) for _ in range(6)]

transformations=[identity,NB,swap_rg]+randoms
out=dot(image,transformations)

for k in range(9): 
    subplot(3,3,k+1)
    imshow (out[...,k,:])

The modern matmul can do the same thing as the old dot, but the stack of matrix must be take in account. (matmul(image,transformations[:,None]) here).

No doubt that it is better in other contexts.

Salvatoresalvay

Answer 4

The equivalent einsum expressions are:

In [92]: np.einsum('ij,kjm->kim',M,V3).shape
Out[92]: (2, 9, 5)
In [93]: np.einsum('ij,lkjm->lkim',M,V4).shape
Out[93]: (3, 2, 9, 5)

Expressed this way, the dot equivalent, 'ij,lkjm->ilkm', looks just as natural as the 'matmul' equivalent, 'ij,lkjm->lkim'.

Hesperides