Circle/rectangle collision response

Question

So I built some time ago a little Breakout clone, and I wanted to upgrade it a little bit, mostly for the collisions. When I first made it I had a basic "collision" detection between my ball and my brick, which in fact considered the ball as another rectangle. But this created an issue with the edge collisions, so I thought I would change it. The thing is, I found some answers to my problem:

for example this image

and the last comment of this thread : circle/rect collision reaction but i could not find how to compute the final velocity vector.

So far I have :

- Found the closest point on the rectangle,
- created the normal and tangent vectors,

And now what I need is to somehow "divide the velocity vector into a normal component and a tangent component; negate the normal component and add the normal and tangent components to get the new Velocity vector" I'm sorry if this seems terribly easy but I could not get my mind around that ... code :

function collision(rect, circle){
  var NearestX = Max(rect.x, Min(circle.pos.x, rect.x + rect.w));
  var NearestY = Max(rect.y, Min(circle.pos.y, rect.y + rect.w));

  var dist = createVector(circle.pos.x - NearestX, circle.pos.y - NearestY);
  var dnormal = createVector(- dist.y, dist.x);
//change current circle vel according to the collision response
}

Thanks !

EDIT: Also found this but I didn't know if it is applicable at all points of the rectangle or only the corners.

Throb

I'm not sure what sort of rect object you are using, but I have a feeling that in your calculation of NearestY, you want the height rather than the width, like rect.h rather than rect.w? – Willms

Answer 1

Best explained with a couple of diagrams:

Have angle of incidence = angle of reflection. Call this value θ.

Have θ = normal angle - incoming angle.

atan2 is the function for computing the angle of a vector from the positive x-axis.

Then the code below immediately follows:

function collision(rect, circle){
  var NearestX = Max(rect.x, Min(circle.pos.x, rect.x + rect.w));
  var NearestY = Max(rect.y, Min(circle.pos.y, rect.y + rect.h));

  var dist = createVector(circle.pos.x - NearestX, circle.pos.y - NearestY);
  var dnormal = createVector(- dist.y, dist.x);

  var normal_angle = atan2(dnormal.y, dnormal.x);
  var incoming_angle = atan2(circle.vel.y, circle.vel.x);
  var theta = normal_angle - incoming_angle;
  circle.vel = circle.vel.rotate(2*theta);
}

Another way of doing it is to get the velocity along the tangent and then subtracting twice this value from the circle velocity.

Then the code becomes

function collision(rect, circle){
  var NearestX = Max(rect.x, Min(circle.pos.x, rect.x + rect.w));
  var NearestY = Max(rect.y, Min(circle.pos.y, rect.y + rect.h));

  var dist = createVector(circle.pos.x - NearestX, circle.pos.y - NearestY);
  var tangent_vel = dist.normalize().dot(circle.vel);
  circle.vel = circle.vel.sub(tangent_vel.mult(2));
}

Both of the code snippets above do basically the same thing in about the same time (probably). Just pick whichever one you best understand.

Also, as @arbuthnott pointed out, there's a copy-paste error in that NearestY should use rect.h instead of rect.w.

Edit: I forgot the positional resolution. This is the process of moving two physics objects apart so that they're no longer intersecting. In this case, since the block is static, we only need to move the ball.

function collision(rect, circle){
  var NearestX = Max(rect.x, Min(circle.pos.x, rect.x + rect.w));
  var NearestY = Max(rect.y, Min(circle.pos.y, rect.y + rect.h));    
  var dist = createVector(circle.pos.x - NearestX, circle.pos.y - NearestY);

  if (circle.vel.dot(dist) < 0) { //if circle is moving toward the rect
    //update circle.vel using one of the above methods
  }

  var penetrationDepth = circle.r - dist.mag();
  var penetrationVector = dist.normalise().mult(penetrationDepth);
  circle.pos = circle.pos.sub(penetrationVector);
}

Andrel

Thanks for that answer I'll definitely try this out ! And for the rect.w/rect.h, this is not a copy paste error, in my case my "rectangles" are in fact squares, so only 1 value is enough, and i kept rect.w ! – Throb

Ok so as far as i've tested (meaning the 1st method), it works well, thank you very much ! I have another problem though, in the game i have multiple rectangles/squares/tiles next to the other, and when the ball hits an intersection, it goes in between the tiles, and glitches inside all the near intersections, any idea how to fix it ? Maybe add conditions about following/preceding tiles for the calculation ? – Throb

Ah, I forgot the positional resolution. See edited answer. This usually ends up still being jittery in places but it's usually a lot better. – Andrel

Thanks for the edit, although for some reasons in my case the positional resolution made things worse (multiple collisions detected, not good when counting points ...) so i just removed the last 3 lines and it works like a charm ! :) Many thanks !! – Throb

Hmm, there's a mistake (or details missing) in the second code block, right? tangent_vel is a dot product (i.e. a number), and it is subtracted from the circle's velocity vector. – Mycenae

Answer 2

Bat and Ball collision

The best way to handle ball and rectangle collision is to exploit the symmetry of the system.

Ball as a point.

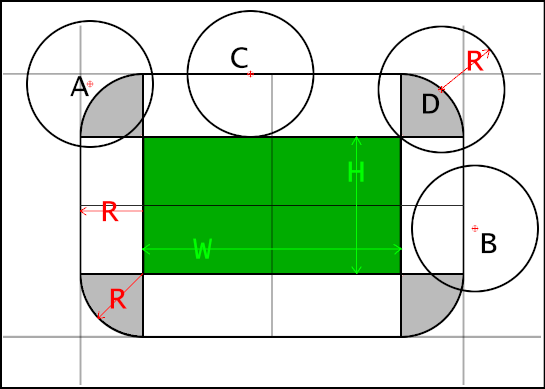
First the ball, it has a radius r that defines all the points r distance from the center. But we can turn the ball into a point and add to the rectangle the radius. The ball is now just a single point moving over time, which is a line.

The rectangle has grown on all sides by radius. The diagram shows how this works.

The green rectangle is the original rectangle. The balls A,B are not touching the rectangle, while the balls C,D are touching. The balls A,D represent a special case, but is easy to solve as you will see.

All motion as a line.

So now we have a larger rectangle and a ball as a point moving over time (a line), but the rectangle is also moving, which means over time the edges will sweep out areas which is too complicated for my brain, so once again we can use symmetry, this time in relative movement.

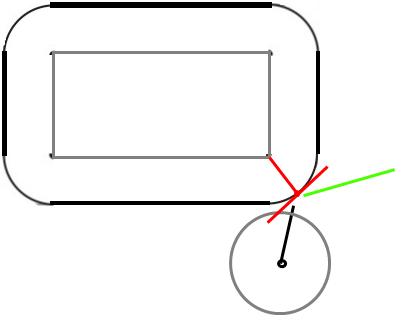
From the bat's point of view it is stationary while the ball is moving, and from the ball, it is still while the bat is moving. They both see each other move in the opposite directions.

As the ball is now a point, making changes to its movement will only change the line it travels along. So we can now fix the bat in space and subtract its movement from the ball. And as the bat is now fixed we can move its center point to the origin, (0,0) and move the ball in the opposite direction.

At this point we make an important assumption. The ball and bat are always in a state that they are not touching, when we move the ball and/or bat then they may touch. If they do make contact we calculate a new trajectory so that they are not touching.

Two possible collisions

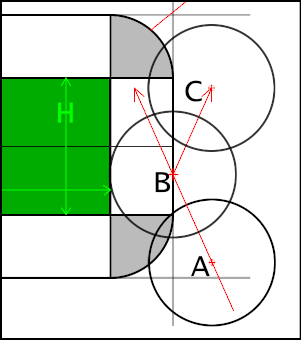
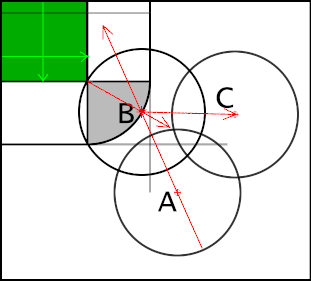
There are now two possible collision cases, one where the ball hits the side of the bat, and one where the ball hits the corner of the bat.

The next images show the bat at the origin and the ball relative to the bat in both motion and position. It is travelling along the red line from A to B then bounces off to C

Ball hits edge

Ball hits corner

As there is symmetry here as well which side or corner is hit does not make any difference. In fact we can mirror the whole problem depending on which size the ball is from the center of the bat. So if the ball is left of the bat then mirror its position and motion in the x direction, and the same for the y direction (you must keep track of this mirror via a semaphore so you can reverse it once the solution is found).

Code

The example does what is described above in the function doBatBall(bat, ball) The ball has some gravity and will bounce off of the sides of the canvas. The bat is moved via the mouse. The bats movement will be transferred to the ball, but the bat will not feel any force from the ball.

const ctx = canvas.getContext("2d");
const mouse  = {x : 0, y : 0, button : false}
function mouseEvents(e){
	mouse.x = e.pageX;
	mouse.y = e.pageY;
	mouse.button = e.type === "mousedown" ? true : e.type === "mouseup" ? false : mouse.button;
}
["down","up","move"].forEach(name => document.addEventListener("mouse" + name, mouseEvents));
								
// short cut vars 
var w = canvas.width;
var h = canvas.height;
var cw = w / 2;  // center 
var ch = h / 2;
const gravity = 1;


// constants and helpers
const PI2 = Math.PI * 2;
const setStyle = (ctx,style) => { Object.keys(style).forEach(key=> ctx[key] = style[key] ) };

// the ball
const ball = {
    r : 50,
    x : 50,
    y : 50,
    dx : 0.2,
    dy : 0.2,
    maxSpeed : 8,
    style : {
        lineWidth : 12,
        strokeStyle : "green",
    },
    draw(ctx){
        setStyle(ctx,this.style);
        ctx.beginPath();
        ctx.arc(this.x,this.y,this.r-this.style.lineWidth * 0.45,0,PI2);
        ctx.stroke();
    },
    update(){
        this.dy += gravity;
        var speed = Math.sqrt(this.dx * this.dx + this.dy * this.dy);
        var x = this.x + this.dx;
        var y = this.y + this.dy;
        
        if(y > canvas.height - this.r){
             y = (canvas.height - this.r) - (y - (canvas.height - this.r));
             this.dy = -this.dy;
        }
        if(y < this.r){
             y = this.r - (y - this.r);
             this.dy = -this.dy;
        }
        if(x > canvas.width - this.r){
             x = (canvas.width - this.r) - (x - (canvas.width - this.r));
             this.dx = -this.dx;
        }
        if(x < this.r){
             x = this.r - (x - this.r);
             this.dx = -this.dx;
        }
        
        this.x = x;
        this.y = y;
        if(speed > this.maxSpeed){  // if over speed then slow the ball down gradualy
            var reduceSpeed = this.maxSpeed + (speed-this.maxSpeed) * 0.9; // reduce speed if over max speed
            this.dx = (this.dx / speed) * reduceSpeed;
            this.dy = (this.dy / speed) * reduceSpeed;
        }
        
        
    }
}
const ballShadow = { // this is used to do calcs that may be dumped
    r : 50,
    x : 50,
    y : 50,
    dx : 0.2,
    dy : 0.2,
}
// Creates the bat
const bat = {
    x : 100,
    y : 250,
    dx : 0,
    dy : 0,
    width : 140,
    height : 10,
    style : {
        lineWidth : 2,
        strokeStyle : "black",
    },
    draw(ctx){
        setStyle(ctx,this.style);
        ctx.strokeRect(this.x - this.width / 2,this.y - this.height / 2, this.width, this.height);
    },
    update(){
        this.dx = mouse.x - this.x;
        this.dy = mouse.y - this.y;        
        var x = this.x + this.dx;
        var y = this.y + this.dy;
        x < this.width / 2  && (x = this.width / 2);
        y < this.height / 2  && (y = this.height / 2);
        x > canvas.width - this.width / 2  && (x = canvas.width  - this.width / 2);
        y > canvas.height - this.height / 2  && (y = canvas.height - this.height / 2);        
        this.dx = x - this.x;
        this.dy = y - this.y;
        this.x = x;
        this.y = y;
        
    }
}

//=============================================================================
// THE FUNCTION THAT DOES THE BALL BAT sim.
// the ball and bat are at new position
function doBatBall(bat,ball){
    var mirrorX = 1;
    var mirrorY = 1;

    const s = ballShadow; // alias
    s.x = ball.x;
    s.y = ball.y;
    s.dx = ball.dx;
    s.dy = ball.dy;
    s.x -= s.dx;
    s.y -= s.dy;

    // get the bat half width height
    const batW2 = bat.width / 2;
    const batH2 = bat.height / 2;  

    // and bat size plus radius of ball
    var batH = batH2 + ball.r;
    var batW = batW2 + ball.r;

    // set ball position relative to bats last pos
    s.x -= bat.x;
    s.y -= bat.y;
    
    // set ball delta relative to bat
    s.dx -= bat.dx;
    s.dy -= bat.dy;
    
    // mirror x and or y if needed
    if(s.x < 0){
        mirrorX = -1;
        s.x = -s.x;
        s.dx = -s.dx;
    }
    if(s.y < 0){
        mirrorY = -1;
        s.y = -s.y;
        s.dy = -s.dy;
    }
    
    
    // bat now only has a bottom, right sides and bottom right corner
    var distY = (batH - s.y); // distance from bottom 
    var distX = (batW - s.x); // distance from right

    if(s.dx > 0 && s.dy > 0){ return }// ball moving away so no hit

    var ballSpeed = Math.sqrt(s.dx * s.dx + s.dy * s.dy); // get ball speed relative to bat

    // get x location of intercept for bottom of bat
    var bottomX = s.x +(s.dx / s.dy) * distY;

    // get y location of intercept for right of bat
    var rightY = s.y +(s.dy / s.dx) * distX;

    // get distance to bottom and right intercepts
    var distB = Math.hypot(bottomX - s.x, batH - s.y);
    var distR = Math.hypot(batW - s.x, rightY - s.y);
    var hit = false;

    if(s.dy < 0 && bottomX <= batW2 && distB <= ballSpeed && distB < distR){  // if hit is on bottom and bottom hit is closest
        hit = true;     
        s.y = batH - s.dy * ((ballSpeed - distB) / ballSpeed);
        s.dy = -s.dy;
    }
    if(! hit && s.dx < 0 && rightY <= batH2 && distR <= ballSpeed && distR <= distB){ // if hit is on right and right hit is closest
        hit = true;     
        s.x =  batW  - s.dx * ((ballSpeed - distR) / ballSpeed);;
        s.dx = -s.dx;
    }
    if(!hit){  // if no hit may have intercepted the corner. 
        // find the distance that the corner is from the line segment from the balls pos to the next pos
        const u = ((batW2 - s.x) * s.dx + (batH2 - s.y) * s.dy)/(ballSpeed * ballSpeed);
        
        // get the closest point on the line to the corner
        var cpx = s.x + s.dx * u;
        var cpy = s.y + s.dy * u;
        
        // get ball radius squared
        const radSqr = ball.r * ball.r;
        
        // get the distance of that point from the corner squared
        const dist  = (cpx - batW2) * (cpx - batW2) + (cpy - batH2) * (cpy - batH2);
        
        // is that distance greater than ball radius
        if(dist > radSqr){ return }  // no hit

        // solves the triangle from center to closest point on balls trajectory
        var d = Math.sqrt(radSqr - dist) / ballSpeed;

        // intercept point is closest to line start
        cpx -= s.dx * d;
        cpy -= s.dy * d;
        
        // get the distance from the ball current pos to the intercept point
        d = Math.hypot(cpx - s.x,cpy - s.y);
        
        // is the distance greater than the ball speed then its a miss
        if(d > ballSpeed){  return  } // no hit return
        
        s.x = cpx;  // position of contact
        s.y = cpy;        
        
        // find the normalised tangent at intercept point 
        const ty = (cpx - batW2) / ball.r;
        const tx = -(cpy - batH2) / ball.r;
        
        // calculate the reflection vector
        const bsx = s.dx / ballSpeed;   // normalise ball speed
        const bsy = s.dy / ballSpeed;
        const dot = (bsx * tx + bsy * ty) * 2;
        
        // get the distance the ball travels past the intercept
        d = ballSpeed - d;
        
        // the reflected vector is the balls new delta (this delta is normalised)
        s.dx = (tx * dot - bsx); 
        s.dy = (ty * dot - bsy);
        
        // move the ball the remaining distance away from corner
        s.x += s.dx * d;
        s.y += s.dy * d;        
        
        // set the ball delta to the balls speed
        s.dx *= ballSpeed;
        s.dy *= ballSpeed;
        hit = true;
    }
    
    // if the ball hit the bat restore absolute position
    if(hit){
        // reverse mirror
        s.x *= mirrorX;
        s.dx *= mirrorX;
        s.y *= mirrorY;
        s.dy *= mirrorY;

        // remove bat relative position
        s.x += bat.x;
        s.y += bat.y;
        
        // remove bat relative delta
        s.dx += bat.dx;
        s.dy += bat.dy;
        
        // set the balls new position and delta
        ball.x = s.x;
        ball.y = s.y;
        ball.dx = s.dx;
        ball.dy = s.dy;
    }
    
}





// main update function
function update(timer){

    if(w !== innerWidth || h !== innerHeight){
      cw = (w = canvas.width = innerWidth) / 2;
      ch = (h = canvas.height = innerHeight) / 2;
    }
      
  
    
    ctx.setTransform(1,0,0,1,0,0); // reset transform
    ctx.globalAlpha = 1;           // reset alpha
    ctx.clearRect(0,0,w,h);
    
    // move bat and ball
    bat.update();
    ball.update();
    
    // check for bal bat contact and change ball position and trajectory if needed
    doBatBall(bat,ball);        

    // draw ball and bat
    bat.draw(ctx);
    ball.draw(ctx);
   
    requestAnimationFrame(update);

}
requestAnimationFrame(update);

canvas { position : absolute; top : 0px; left : 0px; }
body {font-family : arial; }

Use the mouse to move the bat and hit the ball.
<canvas id="canvas"></canvas>

Flaws with this method.

It is possible to trap the ball with the bat such that there is no valid solution, such as pressing the ball down onto the bottom of the screen. At some point the balls diameter is greater than the space between the wall and the bat. When this happens the solution will fail and the ball will pass through the bat.

In the demo there is every effort made to not loss energy, but over time floating point errors will accumulate, this can lead to a loss of energy if the sim is run without some input.

As the bat has infinite momentum it is easy to transfer a lot of energy to the ball, to prevent the ball accumulating to much momentum I have added a max speed to the ball. if the ball moves quicker than the max speed it is gradually slowed down until at or under the max speed.

On occasion if you move the bat away from the ball at the same speed, the extra acceleration due to gravity can result in the ball not being pushed away from the bat correctly.

Quartermaster

I really like this explanation, although I think OP's method of finding the collision point was far simpler. – Andrel

@Andrel Thanks, and Doh I overkilled this answer. Also ran short on time when writing and hacked the corner collision intercept as I went, ended up doing a circle ray intercept then find the reflection, will fix it when i get a chance. What I did not see is that the OP was not after a ball and moving bat, but rather a ball and brick (bricks dont move) so my answer is way overkill (unless the bricks start moving), i was thinking of even adding spin to the ball collision (glad I skipped that).Oh well keeps my geometry maths in practice. – Quartermaster

@Quartermaster I am also looking for what OP was originally looking for. Is it possible we could get a modified version of this with the wall not moving? – Roue

Update: I ported your pure JS example into P5JS (editor.p5js.org/Lathryx/sketches/Brcf0Et0K) and made the walls reduce the velocity of the ball to counteract the issue with the "bat" having "infinite velocity". I'm currently working on a game and I've been looking for a circle-rectangle collision that accurately calculates the corner edge cases, as this is what I have right now: editor.p5js.org/Lathryx/sketches/WfnQgurCR Your answer here is the closest I've seen to this, so I'm trying to reimplement your idea into my physics. Let me know your thoughts! – Roue

Answer 3

Correction of an idea shared above, with adjusting velocity after collision using tangental velocity.

bounciness - constant defined to represent lost force after collision

nv = vector                            # normalized vector from center of cricle to collision point        (normal)
pv = [-vector[1], vector[0]]           # normalized vector perpendicular to nv                             (tangental)
n = dot_product(nv, circle.vel)        # normal vector length
t = dot_product(pv, circle.vel)        # tangental_vector length
new_v = sum_vectors(multiply_vector(t*bounciness, pv), multiply_vector(-n*self.bounciness, nv))            # new velocity vector
circle.velocity = new_v

Selfservice