How to compute perplexity using KenLM?

Question

Let's say we build a model on this:

$ wget https://gist.githubusercontent.com/alvations/1c1b388456dc3760ffb487ce950712ac/raw/86cdf7de279a2b9bceeb3adb481e42691d12fbba/something.txt
$ lmplz -o 5 < something.txt > something.arpa

From the perplexity formula (https://web.stanford.edu/class/cs124/lec/languagemodeling.pdf)

Applying the sum of inverse log formula to get the inner variable and then taking the nth root, the perplexity number is unusually small:

>>> import kenlm
>>> m = kenlm.Model('something.arpa')

# Sentence seen in data.
>>> s = 'The development of a forward-looking and comprehensive European migration policy,'
>>> list(m.full_scores(s))
[(-0.8502398729324341, 2, False), (-3.0185394287109375, 3, False), (-0.3004383146762848, 4, False), (-1.0249041318893433, 5, False), (-0.6545327305793762, 5, False), (-0.29304179549217224, 5, False), (-0.4497605562210083, 5, False), (-0.49850910902023315, 5, False), (-0.3856896460056305, 5, False), (-0.3572353720664978, 5, False), (-1.7523181438446045, 1, False)]
>>> n = len(s.split())
>>> sum_inv_logs = -1 * sum(score for score, _, _ in m.full_scores(s))
>>> math.pow(sum_inv_logs, 1.0/n)
1.2536033936438895

Trying again with a sentence not found in the data:

# Sentence not seen in data.
>>> s = 'The European developement of a forward-looking and comphrensive society is doh.'
>>> sum_inv_logs = -1 * sum(score for score, _, _ in m.full_scores(s))
>>> sum_inv_logs
35.59524390101433
>>> n = len(s.split())
>>> math.pow(sum_inv_logs, 1.0/n)
1.383679905428275

And trying again with totally out of domain data:

>>> s = """On the evening of 5 May 2017, just before the French Presidential Election on 7 May, it was reported that nine gigabytes of Macron's campaign emails had been anonymously posted to Pastebin, a document-sharing site. In a statement on the same evening, Macron's political movement, En Marche!, said: "The En Marche! Movement has been the victim of a massive and co-ordinated hack this evening which has given rise to the diffusion on social media of various internal information"""
>>> sum_inv_logs = -1 * sum(score for score, _, _ in m.full_scores(s))
>>> sum_inv_logs
282.61719834804535
>>> n = len(list(m.full_scores(s)))
>>> n
79
>>> math.pow(sum_inv_logs, 1.0/n)
1.0740582373271952

Although, it is expected that the longer sentence has lower perplexity, it's strange that the difference is less than 1.0 and in the range of decimals.

Is the above the right way to compute perplexity with KenLM? If not, does anyone know how to computer perplexity with the KenLM through the Python API?

Latvia

Answer 1

See https://github.com/kpu/kenlm/blob/master/python/kenlm.pyx#L182

import kenlm

model=kenlm.Model("something.arpa") 
per=model.perplexity("your text sentance")

print(per)

Fantinlatour

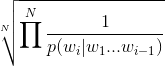
Might not be optimal for all perplexity computation but yes the python wrapper for kenlm has the sentence perplexity pre-coded. – Latvia

Answer 2

The perplexity formula is:

But that's taking the raw probability, so in code:

 import numpy as np
 import kenlm
 m = kenlm.Model('something.arpa')
 # Because the score is in log base 10, so:
 product_inv_prob = np.prod([math.pow(10.0, score) for score, _, _ in m.full_scores(s)])
 n = len(list(m.full_scores(s)))
 perplexity = math.pow(product_inv_prob, 1.0/n)

Or using the log (base 10) prob directly:

 sum_inv_logprob = -1 * sum(score for score, _, _ in m.full_scores(s))
 n = len(list(m.full_scores(s)))
 perplexity = math.pow(10.0, sum_inv_logs / n)

Source: https://www.mail-archive.com/[email protected]/msg15341.html

Latvia

Answer 3

Just want to comment on alvas's answer that

sum_inv_logprob = sum(score for score, _, _ in m.full_scores(s))

Should actually be:

sum_inv_logprob = -1.0 * sum(score for score, _, _ in m.full_scores(s))

Semiconscious

Answer 4

you can simply use

import numpy as np
import kenlm
m = kenlm.Model('something.arpa')
ppl = m.perplexity('something')

Heartstrings

What's the difference with the answer from @Basant Kumar ? https://mcmap.net/q/1872042/-how-to-compute-perplexity-using-kenlm – Dekaliter