Testing whether a line segment intersects a sphere

Question

I am trying to determine whether a line segment (i.e. between two points) intersects a sphere. I am not interested in the position of the intersection, just whether or not the segment intersects the sphere surface. Does anyone have any suggestions as to what the most efficient algorithm for this would be? (I'm wondering if there are any algorithms that are simpler than the usual ray-sphere intersection algorithms, since I'm not interested in the intersection position)

Selwyn

Do you really mean a line segment or an infinite line? All answers refer to infinite lines. – Alurta

Answer 1

I don't know what the standard way of doing it is, but if you only want to know IF it intersects, here is what I would do.

General rule ... avoid doing sqrt() or other costly operations. When possible, deal with the square of the radius.

1. Determine if the starting point is inside the radius of the sphere. If you know that this is never the case, then skip this step. If you are inside, your ray will intersect the sphere.

From here on, your starting point is outside the sphere.

2. Now, imagine the small box that will fit sphere. If you are outside that box, check the x-direction, y-direction and z-direction of the ray to see if it will intersect the side of the box that your ray starts at. This should be a simple sign check, or comparison against zero. If you are outside the and moving away from it, you will never intersect it.

From here on, you are in the more complicated phase. Your starting point is between the imaginary box and the sphere. You can get a simplified expression using calculus and geometry.

The gist of what you want to do is determine if the shortest distance between your ray and the sphere is less than radius of the sphere.

Let your ray be represented by (x0 + it, y0 + jt, z0 + kt), and the centre of your sphere be at (xS, yS, zS). So, we want to find t such that it would give the shortest of (xS - x0 - it, yS - y0 - jt, zS - z0 - kt).

Let x = xS - x0, y = yX - y0, z = zS - z0, D = magnitude of the vector squared

D = x^2 -2*xit + (i*t)^2 + y^2 - 2*yjt + (j*t)^2 + z^2 - 2*zkt + (k*t)^2

D = (i^2 + j^2 + k^2)t^2 - (xi + yj + zk)*2*t + (x^2 + y^2 + z^2)

dD/dt = 0 = 2*t*(i^2 + j^2 + k^2) - 2*(xi + yj + z*k)

t = (xi + yj + z*k) / (i^2 + j^2 + k^2)

Plug t back into the equation for D = .... If the result is less than or equal the square of the sphere's radius, you have an intersection. If it is greater, then there is no intersection.

Lanell

Answer 2

If you are only interested if knowing if it intersects or not then your basic algorithm will look like this...

Consider you have the vector of your ray line, A -> B.

You know that the shortest distance between this vector and the centre of the sphere occurs at the intersection of your ray vector and a vector which is at 90 degrees to this which passes through the centre of the sphere.

You hence have two vectors, the equations of which fully completely defined. You can work out the intersection point of the vectors using linear algebra, and hence the length of the line (or more efficiently the square of the length of the line) and test if this is less than the radius (or the square of the radius) of your sphere.

But

This is the single correct answer on this post. All others are too elaborate. – Ac

Thank you for that. I've been shaking my head at the other higher-ranking answers on this page for a while. Especially ones that start with 'I don't know the standard way of doing this' when the answer I give is the standard way of doing this :-) – But

This answer gives the "aha" moment you're probably looking for. – Saddletree

No, this is not the correct answer, this is only valid for a line. The question explicitly asks for a line segment between two points. – Duvalier

Answer 3

This page has an exact solution for this problem. Essentially, you are substituting the equation for the line into the equation for the sphere, then computes the discriminant of the resulting quadratic. The values of the discriminant indicate intersection.

Consuetudinary

Thanks, I had found this equation somewhere else without much or any explanation of what it did, nice to have a little bit explanation. – Armalda

Updated to a live link. – Consuetudinary

Answer 4

Are you still looking for an answer 13 years later? Here is a complete and simple solution

Assume the following:

• the line segment is defined by endpoints as 3D vectors v1 and v2
• the sphere is centered at vc with radius r

Ne define the three side lengths of a triangle ABC as:

• A = v1-vc
• B = v2-vc
• C = v1-v2

If |A| < r or |B| < r, then we're done; the line segment intersects the sphere

After doing the check above, if the angle between A and B is acute, then we're done; the line segment does not intersect the sphere.

If neither of these conditions are met, then the line segment may or may not intersect the sphere. To find out, we just need to find H, which is the height of the triangle ABC taking C as the base. First we need φ, the angle between A and C:

φ = arccos( dot(A,C) / (|A||C|) )

and then solve for H:

sin(φ) = H/|A|
    ===> H = |A|sin(φ) = |A| sqrt(1 - (dot(A,C) / (|A||C|))^2)

and we are done. The result is

• if H < r, then the line segment intersects the sphere
• if H = r, then the line segment is tangent to the sphere
• if H > r, then the line segment does not intersect the sphere

Here that is in Python:

import numpy as np

def unit_projection(v1, v2):
    '''takes the dot product between v1, v2 after normalization'''
    u1 = v1 / np.linalg.norm(v1)
    u2 = v2 / np.linalg.norm(v2)
    return np.dot(u1, u2)

def angle_between(v1, v2):
    '''computes the angle between vectors v1 and v2'''
    return np.arccos(np.clip(unit_projection(v1, v2), -1, 1))

def check_intersects_sphere(xa, ya, za, xb, yb, zb, xc, yc, zc, radius):
    '''checks if a line segment intersects a sphere'''
    v1 = np.array([xa, ya, za])
    v2 = np.array([xb, yb, zb])
    vc = np.array([xc, yc, zc])
    A = v1 - vc
    B = v2 - vc
    C = v1 - v2

    if(np.linalg.norm(A) < radius or np.linalg.norm(B) < radius): 
        return True
    
    if(angle_between(A, B) < np.pi/2):
        return False

    H = np.linalg.norm(A) * np.sqrt(1 - unit_projection(A, C)**2)
    if(H < radius):
        return True
    if(H >= radius):
        return False

Note that I have written this so that it returns False when either endpoint is on the surface of the sphere, or when the line segment is tangent to the sphere, because it serves my purposes better.

This might be essentially what user Cruachan suggested. A comment there suggests that other answers are "too elaborate". There might be a more elegant way to implement this that uses more compact linear algebra operations and identities, but I suspect that the amount of actual compute required boils down to something like this. If someone sees somewhere to save some effort please do let us know.

---

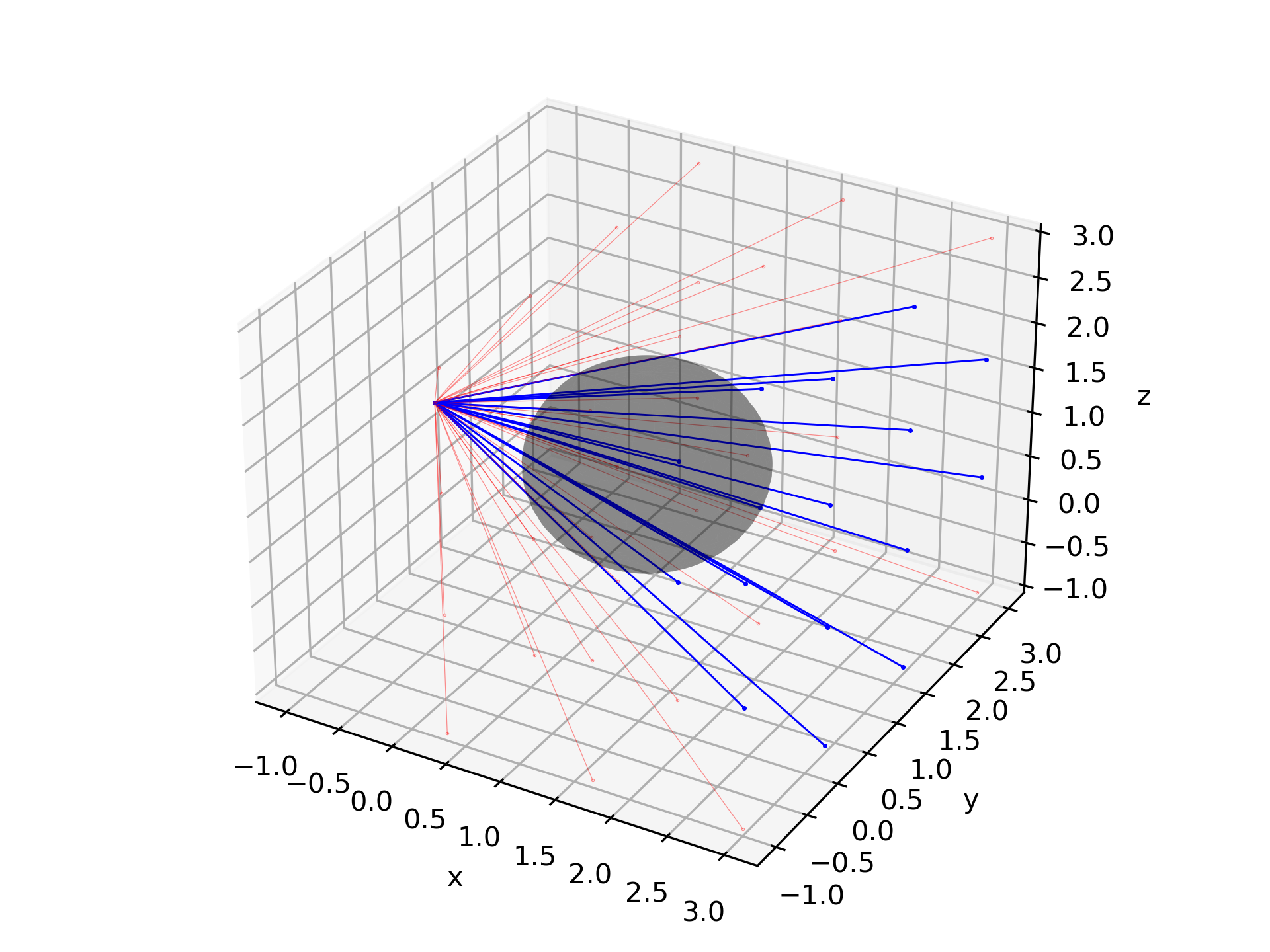
Here is a test of the code. The figure below shows several trial line segments originating from a position (-1, 1, 1) , with a unit sphere at (1,1,1). Blue line segments have intersected, red have not.

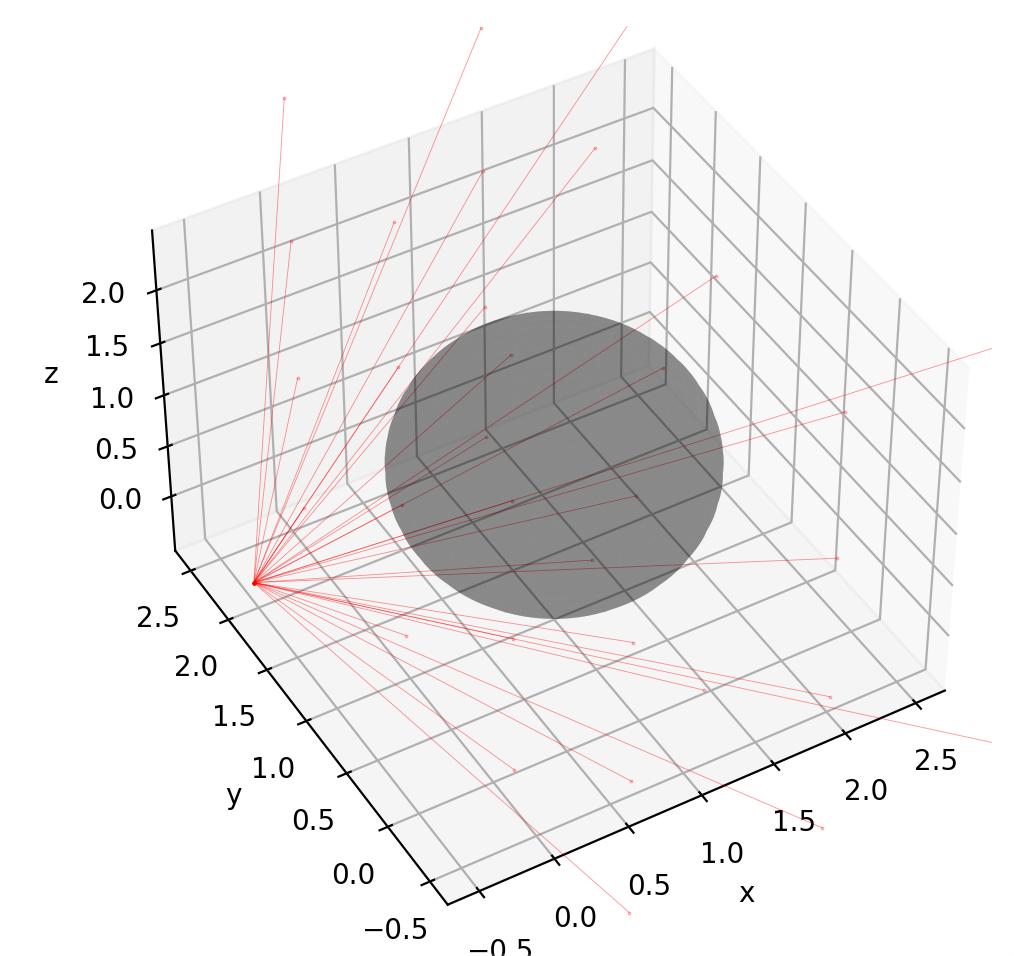
And here is another figure which verifies that line segments that stop just short of the sphere's surface do not intersect, even if the infinite ray that they belong to does:

Here is the code that generates the image:

import matplotlib.pyplot as plt
radius = 1
xc, yc, zc = 1, 1, 1
xa, ya, za = xc-2, yc, zc
nx, ny, nz = 4, 4, 4
xx = np.linspace(xc-2, xc+2, nx)
yy = np.linspace(yc-2, yc+2, ny)
zz = np.linspace(zc-2, zc+2, nz)
n = nx * ny * nz
XX, YY, ZZ = np.meshgrid(xx, yy, zz)
xb, yb, zb = np.ravel(XX), np.ravel(YY), np.ravel(ZZ)

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
for i in range(n):
    if(xb[i] == xa): continue
    intersects = check_intersects_sphere(xa, ya, za, xb[i], yb[i], zb[i], xc, yc, zc, radius)
    color = ['r', 'b'][int(intersects)]
    s = [0.3, 0.7][int(intersects)]
    ax.plot([xa, xb[i]], [ya, yb[i]], [za, zb[i]], '-o', color=color, ms=s, lw=s, alpha=s/0.7)

u = np.linspace(0, 2 * np.pi, 100)
v = np.linspace(0, np.pi, 100)
x = np.outer(np.cos(u), np.sin(v)) + xc
y = np.outer(np.sin(u), np.sin(v)) + yc
z = np.outer(np.ones(np.size(u)), np.cos(v)) + zc
ax.plot_surface(x, y, z,  rstride=4, cstride=4, color='k', linewidth=0, alpha=0.25, zorder=0)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.tight_layout()
plt.show()

Simmonds

Answer 5

If you just need to know whether it intersects, and do not need to know the intersection point, there is a way to do it without much difficulty:

fn intersects(seg: &LineSegment, sphere: &Sphere) -> bool {
    let seg_sq_mag = (seg.b.pos - seg.a.pos).sq_mag();
    
    let sq_dist_to_a = (sphere.center - seg.a.pos).sq_mag();
    let sq_dist_to_b = (sphere.center - seg.b.pos).sq_mag();

    let a_within_sphere = sq_dist_to_a <= sphere.sq_radius;
    let b_within_sphere = sq_dist_to_b <= sphere.sq_radius;
    
    let seg_within_sphere =

        // The segment is within the sphere if either endpoint is within the sphere.
        a_within_sphere ||
        b_within_sphere ||

        // If neither endpoint is within the sphere, the segment is within the sphere iff:
        // 1. The line spanned by the segment passes through the sphere.
        // 2. Two non-overlapping right triangles are formed by each of the segment's endpoints, the center of the sphere,
        //    and the closest point on the line to the sphere. We can confirm this by creating inequalities
        //    using the Pythagorean theorem. 
        {
            let sq_dist_to_line = cross(sphere.center - seg.a.pos, sphere.center - seg.b.pos).sq_mag() / seg_sq_mag;
            let line_passes_through_sphere = sq_dist_to_line <= sphere.sq_radius;
            
            line_passes_through_sphere
            && (sq_dist_to_a - sq_dist_to_line <= seg_sq_mag)
            && (sq_dist_to_b - sq_dist_to_line <= seg_sq_mag)
        };
    
    return seg_within_sphere;
}

Note that this algorithm as formulated above also returns true if the segment is entirely contained in the sphere. I found this useful, but if you do not, just make sure to return false if both endpoints are in the sphere.

v.sq_mag() computes the square magnitude of v.

Working with the square magnitude is more efficient in cases like this since it avoids the need to call sqrt.

cross(a, b) computes the cross product between a and b.

There is one division, but you could refactor to remove it quite easily if you wanted to.

I found the point-line distance formula on Wolfram. There is information there if you want to understand it: https://mathworld.wolfram.com/Point-LineDistance3-Dimensional.html

The last part about the two non-overlapping right triangles can be understood visually:

Wisp

Answer 6

you sorta have to work that the position anyway if you want accuracy. The only way to improve speed algorithmically is to switch from ray-sphere intersection to ray-bounding-box intersection.

Or you could go deeper and try and improve sqrt and other inner function calls

http://wiki.cgsociety.org/index.php/Ray_Sphere_Intersection

Hightoned