- I have the following formula to extend the mathematical expectaion of the original random walk algorithm which is already implemented in SciKit-Image segmentation.
- I tried to implement the Guided random walker algorithm mentioned in this paper by mimicking the Scikit-image implementation.
- but my implementation is not correct because of the mask Array b.
How can I implement the following mathematical expectation correctly?
My code is down.
import numpy as np
import time
import scipy
from scipy import sparse, ndimage as ndi
from scipy.sparse.linalg import cg, spsolve
from skimage import img_as_float
from distutils.version import LooseVersion as Version
import functools
if Version(scipy.__version__) >= Version('1.1'):
cg = functools.partial(cg, atol=0)
try:
from pyamg import ruge_stuben_solver
amg_loaded = True
except ImportError:
amg_loaded = False
def make_graph_edges(image):
if(len(image.shape)==2):
# print(image.shape)
n_x, n_y = image.shape
vertices = np.arange(n_x * n_y ).reshape((n_x, n_y))
edges_horizontal = np.vstack(( vertices[:, :-1].ravel(), vertices[:, 1:].ravel())) # X *(Y-1)
edges_vertical = np.vstack(( vertices[ :-1].ravel(), vertices[1: ].ravel())) #(X-1)* Y
edges = np.hstack((edges_horizontal, edges_vertical))
else:
print('image shape is: ',image.shape)
return edges
#===================================================================================
def compute_weights(image,mask,alpha, beta, eps=1.e-6):
intra_gradients = np.concatenate([np.diff(image, axis=ax).ravel()
for ax in [1, 0] ], axis=0) ** 2 # gradient ^2
# 5-Connected
inter_gradients = np.concatenate([np.diff(mask, axis=ax).ravel()
for ax in [1, 0] ], axis=0)**2
#----------------------------------------
# 1-Connected
# inter_gradients = (image - mask)**2
#----------------------------------------
# Normalize gradients
intra_gradients = (intra_gradients - np.amin(intra_gradients))/(np.amax(intra_gradients)- np.amin(intra_gradients))
inter_gradients = (inter_gradients - np.amin(inter_gradients))/(np.amax(inter_gradients)- np.amin(inter_gradients))
# All dimensions considered together in this standard deviation
#------------------------------------------------------
intra_scale_factor = -beta / (10 * image.std())
intra_weights = np.exp(intra_scale_factor * intra_gradients)
intra_weights += eps
#------------------------------------------------------
inter_scale_factor = -alpha / (10 * image.std())
inter_weights = np.exp(inter_scale_factor * inter_gradients)
inter_weights += eps
#------------------------------------------------------
return -intra_weights, inter_weights # [W_old , w_new]
#=============================================================================
def build_matrices(image, mask, alpha=90, beta=130):
edges_2D = make_graph_edges(image)
intra_weights, inter_weights = compute_weights(image=image,mask=mask,alpha=alpha ,beta=beta, eps=1.e-6 )
#================
# Matrix Laplace
#================
# Build the sparse linear system
pixel_nb = edges_2D.shape[1] # N = n_x * (n_y - 1) * + (n_x - 1) * n_y
i_indices = edges_2D.ravel() # Src - Dest
j_indices = edges_2D[::-1].ravel() # Same list in reverse order ( Dest - Src)
stacked_intra = np.hstack((intra_weights, intra_weights)) # weights (S-->D, D-->S) are same because graph is undirected
lap = sparse.coo_matrix((2*stacked_intra, (i_indices, j_indices)), shape=(pixel_nb, pixel_nb))
lap.setdiag(-2*np.ravel(lap.sum(axis=0)))
# print('Lap',lap.shape)
Laplace = lap.tocsr()
#================
# Matrix Omega
#================
# Build the sparse linear system
stacked_inter = np.hstack((inter_weights, inter_weights)) # weights (S-->D, D-->S) are same because graph is undirected
Omeg = sparse.coo_matrix((2*stacked_inter, (i_indices, j_indices)), shape=(pixel_nb, pixel_nb))
Omeg.setdiag(2*np.ravel((image-mask)**2))
# print('Omeg',Omeg.shape)
Omega = Omeg.tocsr()
#================
# Matrix A
#================
# Build the sparse linear system
weights = Omega.copy()
firstColumn = weights.sum(axis=1)/2
otherColumns = sparse.csr_matrix((weights.shape[0],weights.shape[1]-1))
Mat_A = sparse.hstack((firstColumn, otherColumns))
# print('A',Mat_A.shape)
return Laplace, Omega, Mat_A
#=============================================================================
def build_linear_system(image, labels, nlabels, beta):
"""
Build the matrix A and rhs B of the linear system to solve.
A and B are two blocks of the laplacian of the image graph.
"""
labels2 = labels.copy()
labels = labels.ravel()
indices = np.arange(labels.size) # indices of all vertices
seeds_mask = labels > 0 # Keep only lables withL_out Background
unlabeled_indices = indices[~seeds_mask] # U
seeds_indices = indices[seeds_mask] # M
lap_sparse,omega_sparse, A_sparse = build_matrices(image=image, mask=labels2,
beta=beta)
A_sparse = A_sparse.tocsr()
#-------------------------------------------------------------------------
seeds = labels[seeds_mask]
seeds_mask = sparse.csc_matrix(np.hstack([np.atleast_2d(seeds == lab).T
for lab in range(1, nlabels + 1)]))
#-------------------------------------------------------------------------
# Laplacian
#=============
rows_L = lap_sparse[unlabeled_indices, :]
lap_sparse = rows_L[:, unlabeled_indices] # size = U x U
B_L = -rows_L[:, seeds_indices] # size = N^2(U+M) x U
rhs_L = B_L.dot(seeds_mask)
#-------------------------------------------------------------------------
# Omega
#=============
rows_O = omega_sparse[unlabeled_indices, :]
omega_sparse = rows_O[:, unlabeled_indices] # size = U x U
B_O = -rows_O[:, seeds_indices] # size = N^2(U+M) x U
rhs_O = B_O.dot(seeds_mask)
#-------------------------------------------------------------------------
rows_A = A_sparse[unlabeled_indices, :]
A_sparse = rows_A[:, unlabeled_indices] # size = U x U
B_A = -rows_A[:, seeds_indices] # size = N^2(U+M) x U
rhs_A = B_A.dot(seeds_mask)
#-------------------------------------------------------------------------
return lap_sparse, omega_sparse, A_sparse, rhs_L, rhs_O, rhs_A
#=============================================================================
def solve_linear_system(lap_sparse,omega_sparse,A_sparse, B_L, B_O, B_A,tol):
if not amg_loaded:
print('"cg_mg" not available, it requires pyamg to be installed. ',
'The "cg_j" mode will be used instead.')
#-------------------------------------------------------------------------------
# Laplace
#==========
maxiter = 30
lap_sparse = lap_sparse.tocsr()
mlL = ruge_stuben_solver(lap_sparse)
ML = mlL.aspreconditioner(cycle='V')
cg_L_out_L = [
cg(lap_sparse, B_L[:, i].toarray(), tol=tol, M=ML, maxiter=maxiter)
for i in range(B_L.shape[1])]
if np.any([info > 0 for _, info in cg_L_out_L]):
print("Laplace Conjugate gradient convergence to tolerance not achieved. ",
"\nConsider decreasing beta to improve system conditionning.")
XL = np.asarray([x1 for x1, _ in cg_L_out_L])
#-------------------------------------------------------------------------------
# Omega
#==========
omega_sparse = omega_sparse.tocsr()
mlO = ruge_stuben_solver(omega_sparse)
MO = mlO.aspreconditioner(cycle='V')
maxiter = 30
B_O = np.nan_to_num(B_O)
omega_sparse = np.nan_to_num(omega_sparse)
cg_L_out_O = [
cg(omega_sparse, B_O[:, i].toarray(), tol=tol, M=MO, maxiter=maxiter)
for i in range(B_O.shape[1])]
if np.any([info > 0 for _, info in cg_L_out_O]):
print("Omega Conjugate gradient convergence to tolerance not achieved. ",
"\nConsider decreasing beta to improve system conditionning.")
XO = np.asarray([x1 for x1, _ in cg_L_out_O])
#--------------------------------------------------------------------------------
# Mat_A
#==========
A_sparse = A_sparse.tocsr()
mlA = ruge_stuben_solver(A_sparse)
MA = mlA.aspreconditioner(cycle='V')
maxiter = 30
cg_L_out_A = [
cg(A_sparse, B_A[:, i].toarray(), tol=tol, M=MA, maxiter=maxiter)
for i in range(B_A.shape[1])]
if np.any([info > 0 for _, info in cg_L_out_A]):
print("Mat_A Conjugate gradient convergence to tolerance not achieved. ",
"\nConsider decreasing beta to improve system conditionning.")
XA = np.asarray([x1 for x1, _ in cg_L_out_A])
#--------------------------------------------------------------------------------
return XL, XO, XA
#=======================================================================
def preprocess(labels):
label_values, inv_idx = np.unique(labels, return_inverse=True)
if not (label_values == 0).any():
print('Random walker only segments unlabeled areas, where ',
'\nlabels == 0. No zero valued areas in labels were ',
'\nfound. Returning provided labels.')
return labels, None, None, None, None
# If some labeled pixels are isolated inside pruned zones, prune them
# as well and keep the labels for the final L_output
null_mask = labels == 0
pos_mask = labels > 0
mask = labels >= 0
fill = ndi.binary_propagation(null_mask, mask=mask)
isolated = np.logical_and(pos_mask, np.logical_not(fill))
pos_mask[isolated] = False
# If the array has pruned zones, be sure that no isolated pixels
# exist between pruned zones (they could not be determined)
if label_values[0] < 0 or np.any(isolated):
isolated = np.logical_and(
np.logical_not(ndi.binary_propagation(pos_mask, mask=mask)),
null_mask)
labels[isolated] = -1
if np.all(isolated[null_mask]):
print('All unlabeled pixels are isolated, they could not be ',
'\ndetermined by the random walker algorithm.')
return labels, None, None, None, None
mask[isolated] = False
mask = np.atleast_2d(mask)
else:
mask = None
# Reorder label values to have consecutive integers (no gaps)
zero_idx = np.searchsorted(label_values, 0)
labels = np.atleast_2d(inv_idx.reshape(labels.shape) - zero_idx)
nlabels = label_values[zero_idx + 1:].shape[0]
inds_isolated_seeds = np.nonzero(isolated)
isolated_values = labels[inds_isolated_seeds]
return labels, nlabels, mask, inds_isolated_seeds, isolated_values
#=========================================================================
def random_walker(image, labels, beta=130, gamma=0.4, tol=1.e-3, copy=True, return_full_prob=False):
if (image.ndim !=2):
raise ValueError('For non-multichannel input, image must be of '
'dimension 2.')
if image.shape != labels.shape:
raise ValueError('Incompatible image and labels shapes.')
# image = np.atleast_2d(img_as_float(image))[..., np.newaxis]
image = img_as_float(image)#
labels_shape = labels.shape
labels_dtype = labels.dtype
if copy:
labels = np.copy(labels)
(labels, nlabels, mask,
inds_isolated_seeds, isolated_values) = preprocess(labels)
if isolated_values is None:
# No non isolated zero valued areas in labels were
# found. Returning provided labels.
if return_full_prob:
# Return the concatenation of the masks of each unique label
return np.concatenate([np.atleast_2d(labels == lab)
for lab in np.unique(labels) if lab > 0],
axis=-1)
return labels
# Build the linear system (lap_sparse, B)
lap_sparse,omega_sparse,A_sparse,B_L,B_O,B_A = build_linear_system(image,
labels, nlabels, beta)
# Solve the linear system lap_sparse X = B
# where X[i, j] is the probability that a marker of label i arrives
# first at pixel j by anisotropic diffusion.
XL, XO, XA = solve_linear_system(lap_sparse,omega_sparse,A_sparse, B_L, B_O, B_A,tol)
# Build the L_output according to return_full_prob value
# Put back labels of isolated seeds
labels[inds_isolated_seeds] = isolated_values
labels = labels.reshape(labels_shape)
#-----------------------------------------------------------------------------
if return_full_prob:
mask = labels == 0
#===========#
# Laplacian #
#===========#
L_out = np.zeros((nlabels,) + labels_shape)
for lab, (label_prob_L, prob_L) in enumerate(zip(L_out, XL), start=1):
label_prob_L[mask] = prob_L
label_prob_L[labels == lab] = 1
#===========#
# Omega #
#===========#
O_out = np.zeros((nlabels,) + labels_shape)
for lab, (label_prob_O, prob_O) in enumerate(zip(O_out, XO), start=1):
label_prob_O[mask] = prob_O
label_prob_O[labels == lab] = 1
#===========#
# Mat_A #
#===========#
A_out = np.zeros((nlabels,) + labels_shape)
for lab, (label_prob_A, prob_A) in enumerate(zip(O_out, XO), start=1):
label_prob_A[mask] = prob_O
label_prob_A[labels == lab] = 1
#-----------------------------------------------------------------------------
else:
#===========#
# Laplacian #
#===========#
XL = np.argmax(XL, axis=0) + 1
L_out = labels.astype(labels_dtype)
L_out[labels == 0] = XL
#===========#
# Omega #
#===========#
XO = np.argmax(XO, axis=0) + 1
O_out = labels.astype(labels_dtype)
O_out[labels == 0] = XO
#===========#
# Mat_A #
#===========#
XA = np.argmax(XA, axis=0) + 1
A_out = labels.astype(labels_dtype)
A_out[labels == 0] = XA
#-----------------------------------------------------------------------------
return 0.5*L_out + 0.5*gamma*A_out - 2*O_out

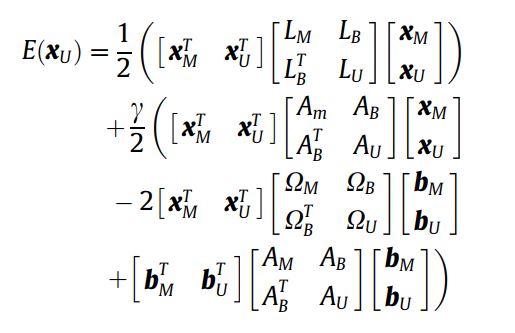
numpy.dotoperations to get the expectation you want? – CaliberXuthe unmarked labels aren't constants, they are variables which has to be minimized, and not calculated directly. – Secretive