How to minimize lasso loss function with scipy.minimize?

Question

Main issue: Why coefficients of Lasso regression are not shrunk to zero with minimization done by scipy.minimize?

I am trying to create Lasso model, using scipy.minimize. However, it is working only when alpha is zero (thus only like basic squared error). When alpha is not zero, it returns worse result (higher loss) and still none of coefficients is zero.

I know that Lasso is not differentiable, but I tried to use Powell optimizer, that should handle non-differential loss (also I tried BFGS, that should handle non-smooth). None of these optimizers worked.

For testing this, I created dataset where y is random (provided here to be reproducible), first feature of X is exactly y*.5 and other four features are random (also provided here to be reproducible). I would expect the algorithm to shrink these random coefficients to zero and keep only the first one, but it's not happening.

For lasso loss function I am using formula from this paper (figure 1, first page)

My code is following:

from scipy.optimize import minimize
import numpy as np

class Lasso:

    def _pred(self,X,w):
        return np.dot(X,w)

    def LossLasso(self,weights,X,y,alpha):
        w = weights
        yp = self._pred(X,w)
        loss = np.linalg.norm(y - yp)**2 + alpha * np.sum(abs(w))
        return loss

    def fit(self,X,y,alpha=0.0):
        initw = np.random.rand(X.shape[1]) #initial weights
        res = minimize(self.LossLasso,
                    initw,
                    args=(X,y,alpha),
                    method='Powell')
        return res

if __name__=='__main__':
    y = np.array([1., 0., 1., 0., 0., 1., 1., 0., 0., 0., 1., 0., 0., 0., 1., 0., 1.,
                  1., 1., 0.])
    X_informative = y.reshape(20,1)*.5
    X_noninformative = np.array([[0.94741352, 0.892991  , 0.29387455, 0.30517762],
                               [0.22743465, 0.66042825, 0.2231239 , 0.16946974],
                               [0.21918747, 0.94606854, 0.1050368 , 0.13710866],
                               [0.5236064 , 0.55479259, 0.47711427, 0.59215551],
                               [0.07061579, 0.80542011, 0.87565747, 0.193524  ],
                               [0.25345866, 0.78401146, 0.40316495, 0.78759134],
                               [0.85351906, 0.39682136, 0.74959904, 0.71950502],
                               [0.383305  , 0.32597392, 0.05472551, 0.16073454],
                               [0.1151415 , 0.71683239, 0.69560523, 0.89810466],
                               [0.48769347, 0.58225877, 0.31199272, 0.37562258],
                               [0.99447288, 0.14605177, 0.61914979, 0.85600544],
                               [0.78071238, 0.63040498, 0.79964659, 0.97343972],
                               [0.39570225, 0.15668933, 0.65247826, 0.78343458],
                               [0.49527699, 0.35968554, 0.6281051 , 0.35479879],
                               [0.13036737, 0.66529989, 0.38607805, 0.0124732 ],
                               [0.04186019, 0.13181696, 0.10475994, 0.06046115],
                               [0.50747742, 0.5022839 , 0.37147486, 0.21679859],
                               [0.93715221, 0.36066077, 0.72510501, 0.48292022],
                               [0.47952644, 0.40818585, 0.89012395, 0.20286356],
                               [0.30201193, 0.07573086, 0.3152038 , 0.49004217]])
    X = np.concatenate([X_informative,X_noninformative],axis=1)

    #alpha zero
    clf = Lasso()
    print(clf.fit(X,y,alpha=0.0))

    #alpha nonzero
    clf = Lasso()
    print(clf.fit(X,y,alpha=0.5))

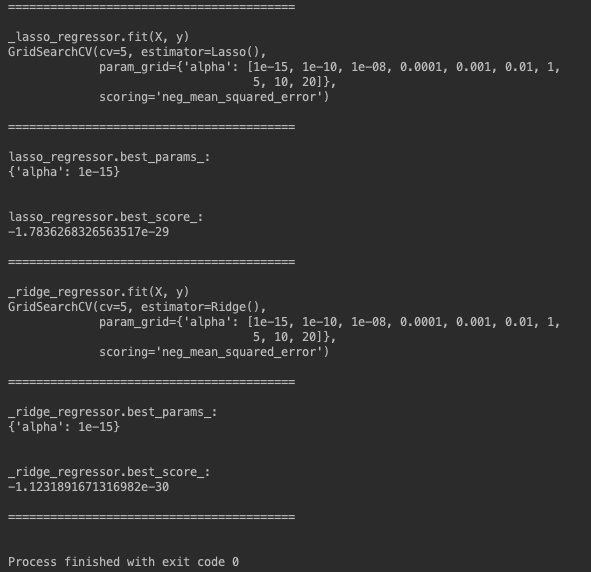
While output of alpha zero is correct:

     fun: 2.1923913945084075e-24
 message: 'Optimization terminated successfully.'
    nfev: 632
     nit: 12
  status: 0
 success: True
       x: array([ 2.00000000e+00, -1.49737205e-13, -5.49916821e-13,  8.87767676e-13,
        1.75335824e-13])

output of alpha non-zero has much higher loss and non of coefficients is zero as expected:

     fun: 0.9714385008821652
 message: 'Optimization terminated successfully.'
    nfev: 527
     nit: 6
  status: 0
 success: True
       x: array([ 1.86644474e+00,  1.63986381e-02,  2.99944361e-03,  1.64568796e-12,
       -6.72908469e-09])

Why coefficients of random features are not shrunk to zero and loss is so high?

Hush

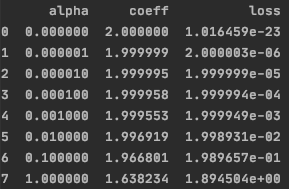
Please post a minimal reproducible example using either a public dataset or a reproducible dummy one, e.g. using scikit-learn's make_regression. – Famed

@Famed sorry, is this ok? (added raw numbers) – Hush

I guess it can do the job – Famed

Answer 1

Is this a viable option:

import numpy as np
from sklearn.linear_model import Lasso, Ridge
from sklearn.model_selection import GridSearchCV

y = np.array([1., 0., 1., 0., 0., 1., 1., 0., 0., 0., 1., 0., 0., 0., 1., 0., 1., 1., 1., 0.])
X_informative = y.reshape(20, 1) * .5

X_noninformative = np.array([[0.94741352, 0.892991  , 0.29387455, 0.30517762],
                           [0.22743465, 0.66042825, 0.2231239 , 0.16946974],
                           [0.21918747, 0.94606854, 0.1050368 , 0.13710866],
                           [0.5236064 , 0.55479259, 0.47711427, 0.59215551],
                           [0.07061579, 0.80542011, 0.87565747, 0.193524  ],
                           [0.25345866, 0.78401146, 0.40316495, 0.78759134],
                           [0.85351906, 0.39682136, 0.74959904, 0.71950502],
                           [0.383305  , 0.32597392, 0.05472551, 0.16073454],
                           [0.1151415 , 0.71683239, 0.69560523, 0.89810466],
                           [0.48769347, 0.58225877, 0.31199272, 0.37562258],
                           [0.99447288, 0.14605177, 0.61914979, 0.85600544],
                           [0.78071238, 0.63040498, 0.79964659, 0.97343972],
                           [0.39570225, 0.15668933, 0.65247826, 0.78343458],
                           [0.49527699, 0.35968554, 0.6281051 , 0.35479879],
                           [0.13036737, 0.66529989, 0.38607805, 0.0124732 ],
                           [0.04186019, 0.13181696, 0.10475994, 0.06046115],
                           [0.50747742, 0.5022839 , 0.37147486, 0.21679859],
                           [0.93715221, 0.36066077, 0.72510501, 0.48292022],
                           [0.47952644, 0.40818585, 0.89012395, 0.20286356],
                           [0.30201193, 0.07573086, 0.3152038 , 0.49004217]])
X = np.concatenate([X_informative,X_noninformative], axis=1)

_lasso = Lasso()
_lasso_parms = {'alpha': [1e-15, 1e-10, 1e-8, 1e-4, 1e-3, 1e-2, 1, 5, 10, 20]}
_lasso_regressor = GridSearchCV(_lasso, _lasso_parms, scoring='neg_mean_squared_error', cv=5)

print('_lasso_regressor.fit(X, y)')
print(_lasso_regressor.fit(X, y))

print("\n=========================================\n")
print('lasso_regressor.best_params_: ')
print(_lasso_regressor.best_params_)
print("\n")
print('lasso_regressor.best_score_: ')
print(_lasso_regressor.best_score_)
print("\n=========================================\n")

_ridge = Ridge()
_ridge_parms = {'alpha': [1e-15, 1e-10, 1e-8, 1e-4, 1e-3, 1e-2, 1, 5, 10, 20]}
_ridge_regressor = GridSearchCV(_ridge, _lasso_parms, scoring='neg_mean_squared_error', cv=5)

print('_ridge_regressor.fit(X, y)')
print(_ridge_regressor.fit(X, y))

print("\n=========================================\n")
print('_ridge_regressor.best_params_: ')
print(_ridge_regressor.best_params_)
print("\n")
print('_ridge_regressor.best_score_: ')
print(_ridge_regressor.best_score_)
print("\n=========================================\n")

and the output:

Gaiter

this shows how to do Lasso using sklearn, however, I need to create Lasso using scipy only, to be able to do some customization to loss function later – Hush

Answer 2

have you tried running the lasso loss minimize with other data sets? with the data you've provided, the regularization (l1 penalty) represents almost the entirety of the loss function's value. as you increase the alpha value, you're increasing the magnitude of the loss function many orders of magnitude above what the loss function returns with the true optimal coefficient 2.0

Provost

Thanks for the idea. However, why should this be a problem? I tried this dataset with Lasso from scikit-learn, and it was able to shrunk all the coefficients to zero, while keeping the first one 2.0. Now I am wondering why this does not work with this scipy Lasso implementation. – Hush

I'm not sure why it would work in scikit-learn and not here, but it might be a clue. You are using the Powell minimization here - did you use an equivalent algorithm in sklearn? The "informative" part of your training data is problematic - it has zero residual when the primary coefficient is 2.0. When I expanded your dataset (numpy stack) and added a random error (numpy random) the effect diminished. Try it yourself. – Provost

I believe that sklearn Lasso uses coordinate descent (at least according to user guide), which is unfortunatelly not present in scipy... – Hush