fit (triple-) gauss to data python

Question

The short version of my problem is the following: I have a histogram of some data (density of planets) which seems to have 3 peeks. Now I want to fit 3 gaussians to this histogram.

I am expecting this outcome.

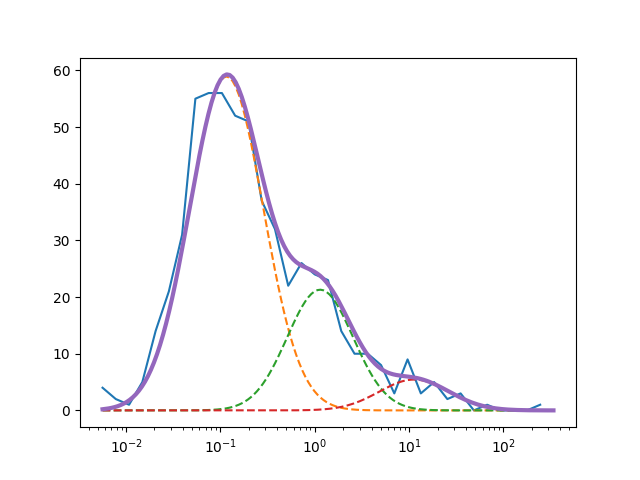
I used different methods to fit my gauss: curve_fit, least square and GaussianMixture from sklearn.mixture. With Curve_fit I get a pretty good fit

but it isn't good enough if you compare it to my expected outcome. With least square I get a "good fit"

but my gaussians are nonsense, and with GaussianMixture I don't get anywhere, because I can't really adept the codes I've seen in Examples to my problem.

At this point I have three questions:

1. Most important: How can I get a better fit for my third gaussian? I already tried to adjust the initial values for p0, but then the gaussian becomes even worst or it doesn't find the parameters at all.

2. What is wrong with my least-square Code? Why does it give me such strange gaussians? And is there a way to fix this? My Guess: Is it because least-square does everything to minimize the error between fit and actual data?

3. How would I do the whole thing with GaussianMixture? I found this post

but couldn't adapt it to my problem.

I really want to understand how to make fits properly, since I will have to do them a lot in the future. The problem is that I am not very good in statistics and just started programming in python.

Here are my three different codes:

Curvefit

import numpy as np
import math
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

hist, bin_edges = np.histogram(Density, bins=np.logspace(np.log10(MIN), np.log10(MAX), 32))

bin_centres = (bin_edges[:-1] + bin_edges[1:])/2

# Define model function to be used to fit to the data above:
def triple_gaussian(  x,*p ):
    (c1, mu1, sigma1, c2, mu2, sigma2, c3, mu3, sigma3) = p
    res =    np.divide(1,x)*c1 * np.exp( - (np.log(x) - mu1)**2.0 / (2.0 * sigma1**2.0) ) \
          +  np.divide(1,x)*c2 * np.exp( - (np.log(x) - mu2)**2.0 / (2.0 * sigma2**2.0) ) \
          +  np.divide(1,x)*c3 * np.exp( - (np.log(x) - mu3)**2.0 / (2.0 * sigma3**2.0) )
    return res

# p0 is the initial guess for the fitting coefficients (A, mu and sigma above)
p0 = [60., 1, 1., 30., 1., 1.,10., 1., 1]

coeff, var_matrix = curve_fit(triple_gaussian, bin_centres, hist, p0=p0)

# Get the fitted curve
hist_fit = triple_gaussian(bin_centres, *coeff)

c1 =coeff[0]
mu1 =coeff[1]
sigma1 =coeff[2]
c2 =coeff[3]
mu2 =coeff[4]
sigma2 =coeff[5]
c3 =coeff[6]
mu3 =coeff[7]
sigma3 =coeff[8]
x= bin_centres

gauss1= np.divide(1,x)*c1 * np.exp( - (np.log(x) - mu1)**2.0 / (2.0 * sigma1**2.0) )
gauss2= np.divide(1,x)*c2 * np.exp( - (np.log(x) - mu2)**2.0 / (2.0 * sigma2**2.0) )
gauss3= np.divide(1,x)*c3 * np.exp( - (np.log(x) - mu3)**2.0 / (2.0 * sigma3**2.0) )

plt.plot(x,gauss1, 'g',label='gauss1')
plt.plot(x,gauss2, 'b', label='gauss2')
plt.plot(x,gauss3, 'y', label='gauss3')
plt.gca().set_xscale("log")
plt.legend(loc='upper right')
plt.ylim([0,70])
plt.suptitle('Triple log Gaussian fit over all Data', fontsize=20)
plt.xlabel('log(Density)')
plt.ylabel('Number')

plt.hist(Density, bins=np.logspace(np.log10(MIN), np.log10(MAX), 32), label='all Densities')
plt.plot(bin_centres, hist, label='Test data')
plt.plot(bin_centres, hist_fit, label='Fitted data')
plt.gca().set_xscale("log") 
plt.ylim([0,70])
plt.suptitle('triple log Gaussian fit using curve_fit', fontsize=20)
plt.xlabel('log(Density)')
plt.ylabel('Number')
plt.legend(loc='upper right')
plt.annotate(Text1, xy=(0.01, 0.95), xycoords='axes fraction')
plt.annotate(Text2, xy=(0.01, 0.90), xycoords='axes fraction')
plt.savefig('all Densities_gauss')
plt.show()

Leastsquare

The fit itselfe doesn't look to bad, but the 3 gaussians are horrible. See here

    # I only have x-data, so to get according y-data I make my histogram and
 #use the bins as x-data and the numbers (hist) as y-data. 
#Density is a Dataset of 581 Values between 0 and 340.

hist, bin_edges = np.histogram(Density, bins=np.logspace(np.log10(MIN), np.log10(MAX), 32))
x = (bin_edges[:-1] + bin_edges[1:])/2
y = hist

#define tripple gaussian

def triple_gaussian(  p,x ):
    (c1, mu1, sigma1, c2, mu2, sigma2, c3, mu3, sigma3) = p
    res =    np.divide(1,x)*c1 * np.exp( - (np.log(x) - mu1)**2.0 / (2.0 * sigma1**2.0) ) \
          +  np.divide(1,x)*c2 * np.exp( - (np.log(x) - mu2)**2.0 / (2.0 * sigma2**2.0) ) \
          +  np.divide(1,x)*c3 * np.exp( - (np.log(x) - mu3)**2.0 / (2.0 * sigma3**2.0) )
    return res

def errfunc(p,x,y):
   return y-triple_gaussian(p,x)

p0=[]
p0 = [60., 0.1, 1., 30., 1., 1.,10., 10., 1.]
fit = optimize.leastsq(errfunc,p0,args=(x,y))

print('fit', fit)



plt.plot(x,y)
plt.plot(x,triple_gaussian(fit[0],x), 'r')
plt.gca().set_xscale("log")
plt.ylim([0,70])
plt.suptitle('Double log Gaussian fit over all Data', fontsize=20)
plt.xlabel('log(Density)')
plt.ylabel('Number')

c1, mu1, sigma1, c2, mu2, sigma2, c3, mu3, sigma3=fit[0]

print('c1', c1)

gauss1= np.divide(1,x)*c1 * np.exp( - (np.log(x) - mu1)**2.0 / (2.0 * sigma1**2.0) )
gauss2= np.divide(1,x)*c2 * np.exp( - (np.log(x) - mu2)**2.0 / (2.0 * sigma2**2.0) )
gauss3= np.divide(1,x)*c3 * np.exp( - (np.log(x) - mu3)**2.0 / (2.0 * sigma3**2.0) )

plt.plot(x,gauss1, 'g')
plt.plot(x,gauss2, 'b')
plt.plot(x,gauss3, 'y')
plt.gca().set_xscale("log")
plt.ylim([0,70])
plt.suptitle('Double log Gaussian fit over all Data', fontsize=20)
plt.xlabel('log(Density)')
plt.ylabel('Number')

GaussianMixture

As I said befor, I don't really understand GaussianMixture. I don't know if I have to define a triplegauss like before, or if it's enough to define the gauss, and GaussianMixture will find out that there is a triple gauss on its own. I also don't understand where I have to use which data, because when I use the bins and hist values, then the "fitted curve" are just the datapoints connected with each other. So I figured that I used the wrong data.

The parts I don't understand are #Fit GMM and #Construct function manually as sum of gaussians.

hist, bin_edges = np.histogram(Density, bins=np.logspace(np.log10(MIN), np.log10(MAX), 32))

bin_centres = (bin_edges[:-1] + bin_edges[1:])/2

plt.hist(Density, bins=np.logspace(np.log10(MIN), np.log10(MAX), 32), label='all Densities')
plt.gca().set_xscale("log") 
plt.ylim([0,70])

# Define simple gaussian
def gauss_function(x, amp, x0, sigma):
    return np.divide(1,x)*amp * np.exp(-(np.log(x) - x0) ** 2. / (2. * sigma ** 2.))

# My Data
samples = Density

# Fit GMM
gmm = GaussianMixture(n_components=3, covariance_type="full", tol=0.00001)
gmm = gmm.fit(X=np.expand_dims(samples, 1))

gmm_x= bin_centres
gmm_y= hist
# Construct function manually as sum of gaussians
gmm_y_sum = np.full_like(gmm_x, fill_value=0, dtype=np.float32)
for m, c, w in zip(gmm.means_.ravel(), gmm.covariances_.ravel(), gmm.weights_.ravel()):
    gauss = gauss_function(x=gmm_x, amp=1, x0=m, sigma=np.sqrt(c))
    gmm_y_sum += gauss / np.trapz(gauss, gmm_x) *w 

# Make regular histogram
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=[8, 5])
ax.hist(samples, bins=np.logspace(np.log10(MIN), np.log10(MAX), 32), label='all Densities')
ax.plot(gmm_x, gmm_y, color="crimson", lw=4, label="GMM")
ax.plot(gmm_x, gmm_y_sum, color="black", lw=4, label="Gauss_sum", linestyle="dashed")
plt.gca().set_xscale("log") 
plt.ylim([0,70])

# Annotate diagram
ax.set_ylabel("Probability density")
ax.set_xlabel("Arbitrary units")

# Make legend
plt.legend()

plt.show()

I hope that anyone can help me at least with one of my questions. As I said befor, if anything is missing or if you need more information please tell me.

Thanks in advance!

--Edit-- Here is my Data.

Kendallkendell

Are your Density values available by any chance? Right now it is not possible to test your code. – Lyricist

I have the Data as txt file, can I upload it somehow? – Kendallkendell

Answer 1

Having a link to actual data would be helpful, but I can make a few recommendations without the data.

First, converting x to np.log(x) is so easy that it is probably worth the effort.

Second, the definition for Gaussian doesn't normally include 1./x -- it might be a small effect, but your values of x are changing by an order of magnitude, so maybe not.

Third, you're providing the same starting value for mu for all three Gaussians. This makes the fit much harder. Try to give starting points that are closer to the actual expected values, and if possible bounds on those values.

To help address these points, you might find lmfit (https://lmfit.github.io/lmfit-py/) helpful. It will definitely make your script shorter, perhaps something like

import numpy as np
import matplotlib.pyplot as plt
from lmfit.models import GaussianModel

y, bin_edges = np.histogram(Density, bins=np.logspace(np.log10(MIN), np.log10(MAX), 32))

x = np.log((bin_edges[:-1] + bin_edges[1:])/2.0) #take log here

# build a model as a sum of 3 Gaussians
model = (GaussianModel(prefix='g1_') + GaussianModel(prefix='g2_') + 
         GaussianModel(prefix='g3_'))

# build Parameters with initial values
params = model.make_params(g1_amplitude=60, g1_center=-1.0, g1_sigma=1,
                           g2_amplitude=30, g2_center= 0.0, g1_sigma=1,
                           g2_amplitude=10, g2_center= 1.0, g1_sigma=1)

# optionally, set bound / constraints on Parameters:
params['g1_center'].max = 0

params['g2_center'].min = -1.0
params['g2_center'].max = 1.0

params['g3_center'].min = 0

# perform the actual fit
result = model.fit(y, params, x=x)

# print fit statistics and values and uncertainties for variables
print(result.fit_report())

# evaluate the model components ('g1_', 'g2_', and 'g3_')
comps = result.eval_components(result.params, x=x)

# plot the results
plt.plot(x, y, label='data')
plt.plot(x, result.best_fit, label='best fit')

plt.plot(x, comps['g1_'], label='gaussian1')
plt.plot(x, comps['g2_'], label='gaussian2')
plt.plot(x, comps['g3_'], label='gaussian3')
# other plt methods for axes and labels
plt.show()

If your model really needs (1/x) times a Gaussian, or you need a different functional form. You could use the built-in LognormalModel, one of the other built-in Models, or easily write your own model function and wrap that.

hope that helps.

Charcoal

Thanks! I get an error with lmfit: ModuleNotFoundError: No module named 'lmfit.models'; 'lmfit' is not a package do i need to install it somehow? I've never done this befor. Also: I use a log-gauss, that's why there is the (1/x) factor. I wanted to upload my data but dont know how (I have it as a .txt file) – Kendallkendell

This is getting off-topic, but yes, you need to install lmfit. Try pip install lmfit or read the docs for how to install Python modules on your system. FWIW, lmfit also has a LognormalModel. Many websites (github gists, google docs) will allow you to post data and then you can provide a link. – Charcoal

Thanks again, I couldn't fix the lmfit problem yet, so I opened a new question. Changing x to np.log(x) didn't solve my problem, and when I change mu to a different value, the solution gets even worst (what suprised me). I added a link to my Data in my Question above, I would be very happy if you could take another look at it. – Kendallkendell

Answer 2

For your specific case there is no difference between summing up three Gaussian or the mixed model, latter one only taking care that the norm is kept. Basically, I just simplified and cleaned up your version. It runs nicely, but be aware that the results depend on the number of bins quite significantly.

import matplotlib.pyplot as plt
import numpy as np
import scipy.optimize as so

data = np.loadtxt( "data.txt" )
myBins = np.logspace( np.log10( min( data ) ), np.log10( max( data ) ), 35 )

""" as we are logarithmic I calculate the bin 'centre' logarithmic as well """
xBins = np.fromiter( ( ( 10**( np.log10( x * y ) / 2. ) ) for x,y in zip( myBins[:-1], myBins[1:] ) ), np.float ) 
vals, bins = np.histogram( data, myBins )

def chunks( l, n ):
    """Yield successive n-sized chunks from l."""
    for i in range( 0, len( l ), n ):
        yield l[ i:i + n ]


"""  I use a simplified version without the 1/x """
def my_gauss( x, c, mu, sig ):
    #~ out = c * np.exp( - ( np.log( x ) - mu )**2.0 / (2.0 * sig**2.0 ) ) * np.divide( 1, x )
    out = c * np.exp( - ( np.log( x ) - mu )**2.0 / (2.0 * sig**2.0 ) )
    return out


def triple_residuals( params, xData, yData ):
    yTh = np.zeros_like( yData, dtype=np.float )
    for params in chunks( params, 3 ) :
        yTh += np.fromiter( ( my_gauss( x, *params ) for x in xData ), np.float )
    diff = yData - yTh
    return diff


sol, err = so.leastsq( triple_residuals, [ 40, -2.1, 1.1, 10, -0.1, 1.1, 10, 2.1, 1.1 ], args=( xBins, vals )  )


myxList = np.logspace( np.log10( min( data ) ), np.log10( max( data ) ), 150 )

""" for guessing start values """
#~ myg1List = np.fromiter( ( my_gauss( x, 40, -2.1, 1.1 ) for x in myxList ), np.float )
#~ myg2List = np.fromiter( ( my_gauss( x, 20, -0.1, 1.2 ) for x in myxList ), np.float )
#~ myg3List = np.fromiter( ( my_gauss( x, 10, 2.1, 1.3 ) for x in myxList ), np.float )


fig = plt.figure()
ax = fig.add_subplot( 1, 1, 1)
ax.plot( bins[:-1], vals )

""" for plotting start values """
#~ ax.plot( myxList,  myg1List )
#~ ax.plot( myxList,  myg2List )
#~ ax.plot( myxList,  myg3List )

gs = dict()
for i,params in enumerate( chunks( sol, 3) ) :
    print params
    gs[i] = np.fromiter( ( my_gauss( x, *params ) for x in myxList ), np.float )
    ax.plot( myxList,  gs[i], ls='--' )

gsAll = gs[0] + gs[1] + gs[2]
ax.plot( myxList,  gsAll, lw=3 )

ax.set_xscale('log')
plt.show()

and provides:

>>[58.91221784 -2.1544611   0.89842033]
>>[21.29816862  0.13135854  0.80339236]
>>[5.44419833 2.42596666 0.85324204]

Flattish