Fitting a local level Poisson (State Space Model)

Question

I am working through "Forecasting with Exponential Smoothing". I am stuck on exercise 16.4 on the part that states:

The data set partx contains a history of monthly sales of an automobile part. Apply a local Poisson model. Parameters should be estimated by either maximizing the likelihood or minimizing the sum of squared errors.

The local Poisson model is defined as:

where and

I have the following code, but it seems to be stuck. The optimization always returns something close to the starting values.

Am I fitting the local Poisson model correctly?

library(expsmooth)
data("partx")
S <- function(x) {
  a <- x[1]
  if(a < 0 | a > 1)
    return(Inf)
  n <- length(partx)
  lambda <- numeric(n+1)
  error <- numeric(n)
  lambda[1] <- x[2]
  for(i in 1:n) {
    error[i] <- partx[i]-rpois(1,lambda[i])
    lambda[i+1] <-   (1-a)*lambda[i] + a*partx[i]
  }
  return(sum(error^2))
}

# returns a = 0.5153971 and lambda = 5.9282414
op1 <- optim(c(0.5,5L),S, control = list(trace = 1))
# returns a = 0.5999655 and lambda = 2.1000131
op2 <- optim(c(0.5,2L),S, control = list(trace = 1))

Waugh

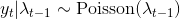
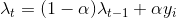
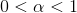
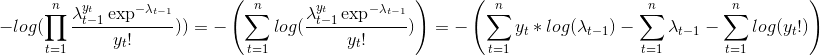
One thing I notice is that rpois(1,lambda[i]) will be doing a random draw from the poisson distribution each time. Every time you rerun the optim you get a different result unless you use set.seed. The expectation of a poisson is lambda, so my gut feeling is to instead write error[i] <- partx[i]-lambda[i], but I could be wrong. Also, you can add lower and upper values to optim for the parameter constraints e.g.op1 <- optim(c(0.5,5L), S, lower=c(0,0), upper=c(1,Inf), method = "L-BFGS-B") – Lightheaded

Answer 1

I know the book says you could use sum of squared errors or MLE but the first option seems wired due too the fact that you have to sample a poison distribution so event if you fix the parameters you would get the different sum of squared errors every time. As you don't say that you have tried the MLE approach I program it. The math is as follows:

And the code that implements it is

MLELocalPoisson = function(par,y){
  alpha = par[1]
  lambda_ini = par[2]
  n = length(y)
  vec_lambda = rep(NA, n)
  for(i in 1:n){
    if(i==1){
      vec_lambda[i] = (1-alpha)*lambda_ini+alpha*y[i]
    }else{
      vec_lambda[i] = (1-alpha)*vec_lambda[i-1]+alpha*y[i]
    }
  }
  vec_lambda = c(lambda_ini,vec_lambda[-n])
  sum_factorial = sum(sapply(y,function(x)log(factorial(x))))
  sum_lambda = sum(vec_lambda)
  sum_prod = sum(log(vec_lambda)*y)
  loglike = -sum_prod+sum_lambda+sum_factorial
  return(loglike)
}
optim(par = c(0.1,1),fn = MLELocalPoisson,y = partx, method = "L-BFGS-B",
      lower=c(1e-10,1e-10),upper = c(1,Inf),control = list(maxit = 10000))

the lower values set a 1e-10 is done so the optimization do not try c(0,0) and thus generating a loglikelihood of NaN.

EDIT

Taking a look at the poisson regression literature the usually define $\lambda = exp(x*\beta)$ and calculate the residuals as $y-exp(x*\beta)$ (have a look at). So it might be possible to do the same in this problem using the formula given by the author for $\lambda$ like this:

LocalPoisson = function(par,y,optim){
  alpha = par[1]
  lambda_ini = par[2]
  n = length(y)
  vec_lambda = rep(NA, n)
  y_hat = rep(NA, n)
  for(i in 1:n){
    if(i==1){
      vec_lambda[i] = (1-alpha)*lambda_ini+alpha*y[i]
    }else{
      vec_lambda[i] = (1-alpha)*vec_lambda[i-1]+alpha*y[i]
    }
  }
  if(optim){
    y_hat = c(lambda_ini,vec_lambda[-n])
    return(sum((y_hat-y)^2))
  } else {
    return(data.frame(y_hat = y_hat,y=y, lambda = vec_lambda))
  }

}
optim(par = c(0.1,1),fn = LocalPoisson,y = partx, optim =T,method = "L-BFGS-B",
                lower=c(1e-10,1e-10),upper = c(1,Inf),control = list(maxit = 10000))

It does not yields the same results as the MLE (and I feel more comfortable with that option but it might be a possible way to estimate the parameters).

Mats