Matlab - Gaussian mixture and Fuzzy C-means less accurate than K-means on high-dimensional data (image of 26-dimension vectors)

Question

I took the matlab code from this tutorial Texture Segmentation Using Gabor Filters.

To test clustering algorithms on the resulting multi-dimensional texture responses to gabor filters, I applied Gaussian Mixture and Fuzzy C-means instead of the K-means to compare their results (number of clusters = 2 in all of the cases):

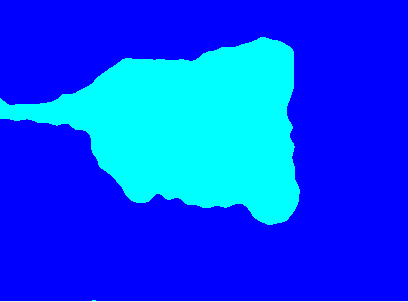
Original image:

K-means clusters:

L = kmeans(X, 2, 'Replicates', 5);

GMM clusters:

options = statset('MaxIter',1000);
gmm = fitgmdist(X, 2, 'Options', options);
L = cluster(gmm, X);

Fuzzy C-means:

[centers, U] = fcm(X, 2);
[values indexes] = max(U);

What I've found weird in this case is that K-means clusters are more accurate than those extracted using GMM and Fuzzy C-means.

Can anyone explain to me if the high-dimensionality (L x W x 26: 26 is the number of gabor filters used) of the data given as input to the GMM and the Fuzzy C-means classifiers is what's causing the clustering to be less accurate?

In other words is the GMM and the Fuzzy C-means clustering more sensitive to the dimensionality of the data, than K-means is?

Corneliacornelian

I don't have the right toolboxes for this, but here are a few observations. All methods are sensitive to initialization, but k-means is cheating by using 5 'Replicates' and higher quality initialization (k-means++). k-means is GMM under a spherical-covariance assumption, so in theory it shouldn't do much better. I think most of the discrepancy comes down to initialization. You should be able to test this by using the k-means result as initial conditions for GMM. – Konya

@Konya You might be right, running those clustering algorithms multiple times seems to yield a different result on every execution. Could you please write it as an answer to receive the bounty? – Corneliacornelian

Answer 1

Glad the comment was useful, here are my observations in answer form.

Each of these methods are sensitive to initialization, but k-means is cheating by using 5 'Replicates' and higher quality initialization (k-means++). The rest of the methods appear to be using a single random initialization.

k-means is GMM if you force spherical covariance. So in theory, it shouldn't do much better (it might do slightly better if the true covariance was in fact spherical).

I think most of the discrepancy comes down to initialization. You should be able to test this by using the k-means result as initial conditions for the other algorithms. Or as you tried, run several times using different random seeds and check if there is more variation in GMM and Fuzzy C-means than there is in k-means.

Konya