minimize byte wasted to align data between 2 headers (custom allocator)

Question

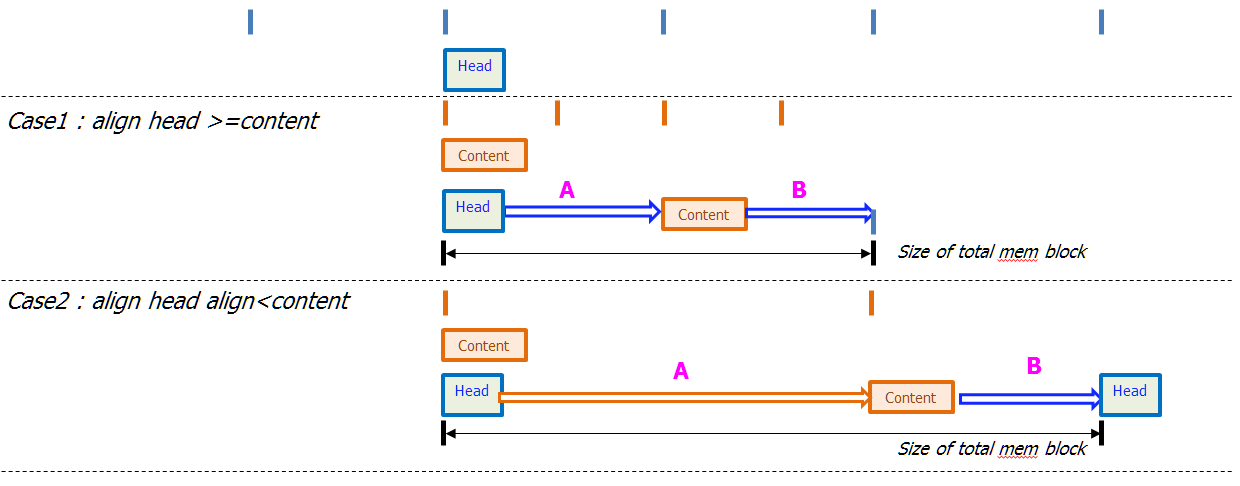
Here is a memory layout within a custom allocator :-

^ toward less address
....
Header                         [size=16     alignment=4      ] ....(1)
some waste space A             [size=A   (unknown)           ]
content                        [size="SIZE" alignment="ALIGN"] ....(2)
some waste space B             [size=B   (unknown)           ]
Header                         [size=16     alignment=4      ] ....(3)
....
v toward more address

The exact address of Header is not known beforehand.
However, I know that :-

every Header address % 4 == 0      from (1,3)
"content"%ALIGN          == 0      from (2)

Question

How to determine minimum amount of byte for A+content+B that make everything (1&2&3) always align appropriately?

I need the result of the function (A+content+B) as a parameter to query a memory block from the custom heap allocator.

//return maximum size of A+content+B that make the allocation always safe
int wasteA_content_wasteB(int SIZE,int ALIGN){
    //???
}

My progress

If I approach the problem in a more Mathematic-way :-

Header                  start at K1*4
some waste space A      
content                 start at K2*ALIGN
some waste space B       
Header                  start at K3*4
//K1 and K2 and K3 are unknown positive integer

I will get an inequality system :-

K1*4 + 16     <= K2*ALIGN
K2*ALIGN+SIZE <= K3*4

However, with my limited Math background, I don't know how to solve it.

The main difficulty is that I don't know K1 in advance.

I will know K1 only after I get that block of memory. :(

Therefore, the result of function may be a little sub-optimal (for safety at the worst-case), but I think it is acceptable.

My current workarounds

If I am very desperate, I can :-

1. query a lot more than need e.g. return ceil((SIZE+max(4,ALIGN)-1)/ALIGN)*ALIGN
2. brute force every possible combination (e.g. loop by SIZE and ALIGN) or calculate every case beforehand then cache it inside a text file.

But it is disgraceful ... I believe there is an explicit formula for this problem. (no?)

I would like an answer that shows concept & idea (show how to think).
Code is not required, but I don't mind.

---

3 years later, Passer By's answer is still useful for me. So, I will paste my interpretation here :-

Bruise

Alignment can be achieved actually by a quite simple formula. E.g. align number of bits to 8 (a full byte): nBitsA = (nBits + 7) / 8 * 8 or even simpler with bit masking: nBitsA = (nBits + 7) & ~0x7. Note that the + 7 is the trick to round up. The rest is provided for free using integer math. – Mond

I'm (really) not sure whether this is appropriate here but 1st I would try to let the compiler do the work: define a struct with the required data layout and then use sizeof and, may be, offsetof. If the defined struct is never instanced this is evaluated by the compiler completely i.e. there will be only "ready computed" constants in the binary code. – Mond

@Scheff Yes, thank! I use that ceiling trick for ::operator new/delete. – Bruise

Answer 1

Let us first assume ALIGN is a power of 2.

There are two cases, one is ALIGN <= 4 and other is ALIGN > 4.

If ALIGN <= 4, then content is always aligned with A == 0 if Header is. All that is left is to pad B until the next header is at alignment == 4. So, A + content + B == ceil(content/4)*4.

If ALIGN > 4, we would need to find consecutive bytes where content can fit in there with alignment of ALIGN.

In the worst case, Header can be located at position k*ALIGN - 12, and hence A would start at k*ALIGN + 4. To find an alignment of ALIGN, you would need A == ALIGN - 4, so A + content == ALIGN + content - 4.

What is left is to pad for the next Header. B starts at k'*ALIGN + content and hence we would require B == 4 - (content%4) since we assumed ALIGN is a power of 2 greater than 4. Thus A + content + B == ALIGN + content + (content%4) or ALIGN + ceil(content/4)*4.

Note that in this solution, the position of content is not static relative to Header.

Youngman

There are two cases <-- That is the word of wisdom, so clever. The whole solution is both accurate and complete. Thank! – Bruise