I wrote a kalman Filter implementation using the Eigen Library in C++ and also using the implementation at this link to test my filter: My prediction step looks like this:
void KalmanFilter::Predict()
{
// state Estimate = state transition matrix * previous state
// No control input present.
x = A * x;
// State Covariance Matrix = (State Transition Matrix * Previous State
Covariance matrix * (State Transition Matrix)^T ) + Process Noise
P = A * P * A.transpose() + Q;
}
while my update step is:
void KalmanFilter::Update(VectorXd z)
{
//Kalman Gain = (State Covariance Matrix * Measurement matrix.transpose) * (H*P*H^T + Measurement Noise)^-1
K = (P * H.transpose()) * (H * P * H.transpose()+ R).inverse();
//Estimated Stated = Estimated state + Kalman Gain (Measurement Innovation)
x = x + K*(z - H * x);
//State Covariance matrix = (Identity Matrix of the size of x.size * x.size) - K* H * P;
long x_size = x.size();
MatrixXd I = MatrixXd::Identity(x_size, x_size);
P = (I - K * H) * P ;
}
My initial values are:
pos_x = 0.0;
pos_y = 0.0;
pos_z = 1.0;
vel_x = 10.0;
vel_y = 0.0;
vel_z = 0.0;
acc_x = 0.0;
acc_y = 0.0;
acc_z = -9.81;
and I'm generating "fake data" by doing the following in a loop:
double c = 0.1; // Drag resistance coefficient
double damping = 0.9 ; // Damping
double sigma_position = 0.1 ; // position_noise
// Create simulated position data
for (int i = 0; i < N; i ++)
{
acc_x = -c * pow(vel_x, 2); // calculate acceleration ( Drag Resistance)
vel_x += acc_x * dt; // Integrate acceleration to give you velocity in the x axis.
pos_x += vel_x * dt; // Integrate velocity to return the position in the x axis
acc_z = -9.806 + c * pow(vel_z, 2); // Gravitation + Drag
vel_z += acc_z * dt; // z axis velocity
pos_z += vel_z * dt; // position in z axis
// generate y position here later.
if(pos_z < 0.01)
{
vel_z = -vel_z * damping;
pos_z += vel_z * dt;
}
if (vel_x < 0.1)
{
acc_x = 0.0;
acc_z = 0.0;
}
// add some noise
pos_x = pos_x + sigma_position * process_noise(generator);
pos_y = pos_y + sigma_position * process_noise(generator);
pos_z = pos_z + sigma_position * process_noise(generator);
I then run my prediction and update step by:
// Prediction Step
kalmanFilter.Predict();
// Correction Step
kalmanFilter.Update(z);
where z is a 3 x 1 vector containing pos_x, pos_y and pos_z
My State Transition Matrix A looks like this:
A << 1, 0, 0, dt, 0, 0, dt_squared, 0 , 0,
0, 1, 0, 0, dt, 0, 0, dt_squared, 0,
0, 0, 1, 0, 0, dt, 0, 0, dt_squared,
0, 0, 0, 1, 0, 0, dt, 0, 0,
0, 0, 0, 0, 1, 0, 0 , dt, 0,
0, 0, 0, 0, 0, 1, 0, 0, dt,
0, 0, 0, 0, 0, 0, 1, 0, 0,
0, 0, 0, 0, 0, 0, 0, 1, 0,
0, 0, 0, 0, 0, 0, 0, 0, 1;
where dt_squared is (dt * dt) /2;
P is
P<< 100, 0, 0, 0, 0, 0, 0, 0, 0,
0, 100, 0, 0, 0, 0, 0, 0, 0,
0, 0, 100, 0, 0, 0, 0, 0, 0,
0, 0, 0, 100, 0, 0, 0, 0, 0,
0, 0, 0, 0, 100, 0, 0, 0, 0,
0, 0, 0, 0, 0, 100, 0, 0, 0,
0, 0, 0, 0, 0, 0, 100, 0, 0,
0, 0, 0, 0, 0, 0, 0, 100, 0,
0, 0, 0, 0, 0, 0, 0, 0, 100;
and
R << 1, 0, 0,
0, 1, 0,
0, 0, 1;
and
Q = G * G.transpose()* a * a;
where G is a 9 x 1 Matrix of
G << dt_squared, dt_squared, dt_squared, dt, dt, dt, 1, 1, 1;
a = 0.1 //( acceleration process noise)
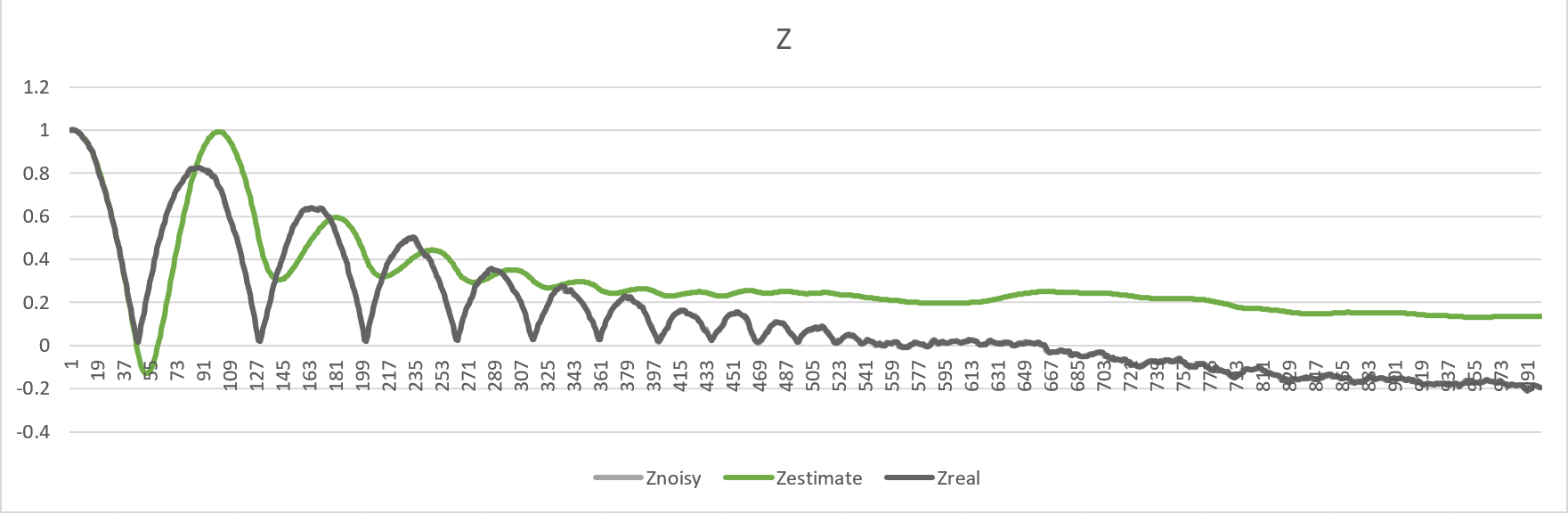
My issue is my estimated position for y and z are off and diverge from the "real" positions. If you look at the following graphs,
This is what pos_x looks like: 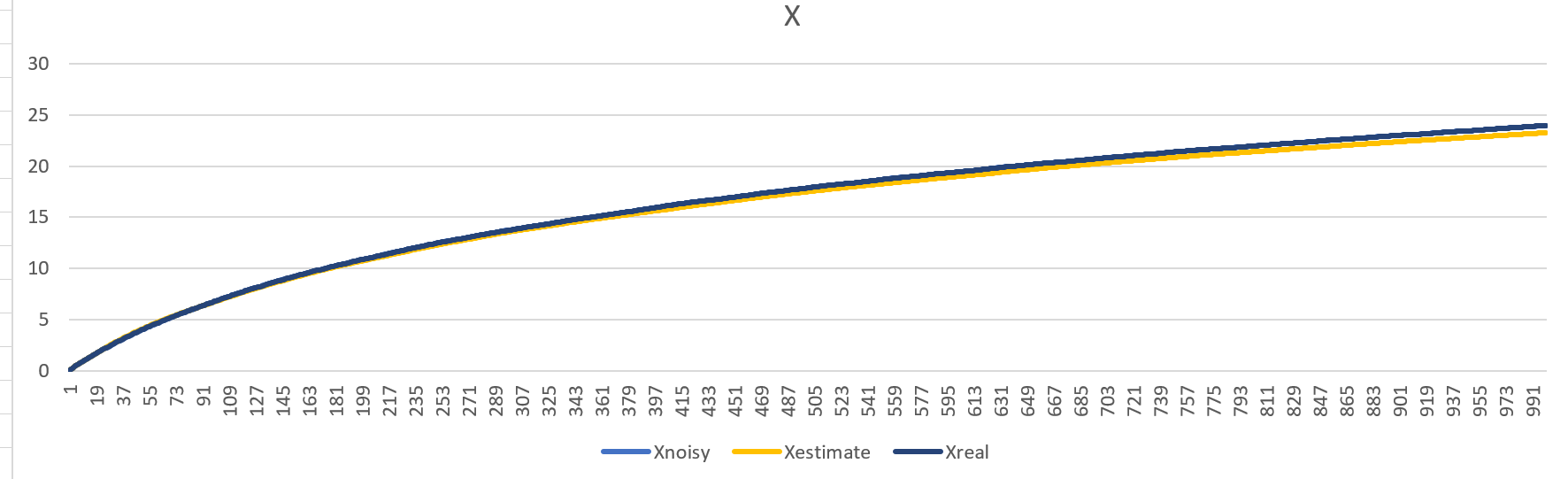
This is what pos_y looks like: 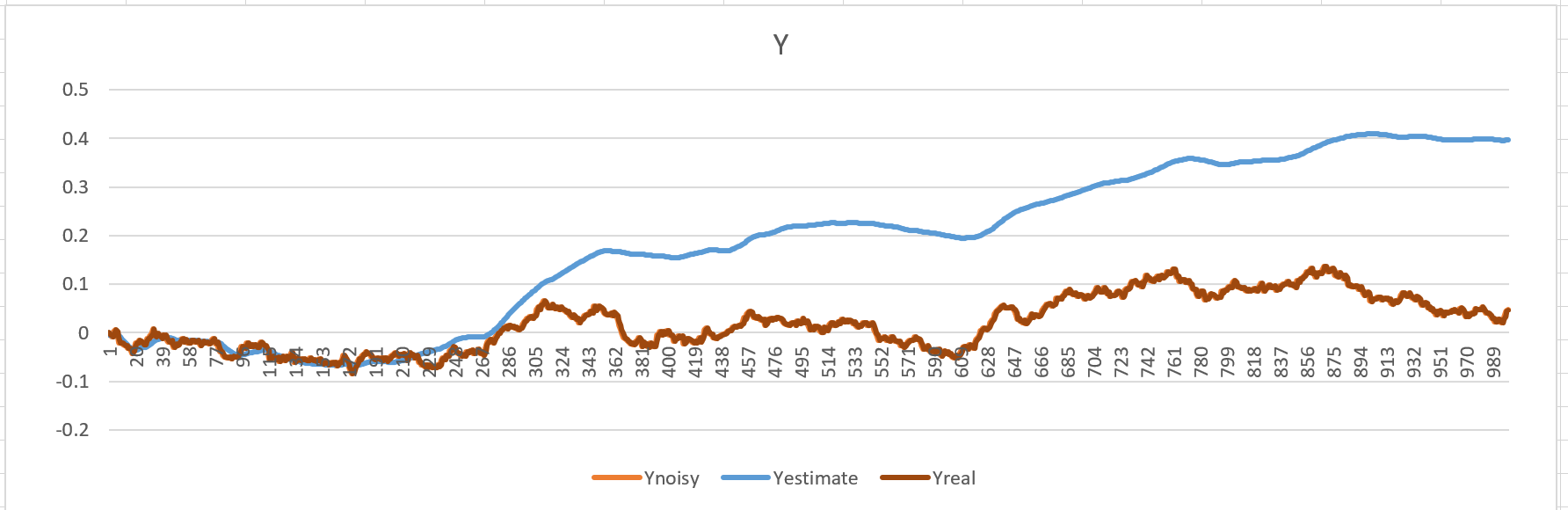
This is my first foray with Kalman filters and I'm not sure what I'm doing wrong here. My final goal would be to use this to estimate the position of a drone. Additionally, I have the following questions:
In a real life situation for a drone for example, how do you about choosing your Process Noise if you can't directly observe the process? Do you simply just pick arbitrary values?
My apologies for the long post. Any help is appreciated.