How to find the order of discrete point-set efficiently?

Question

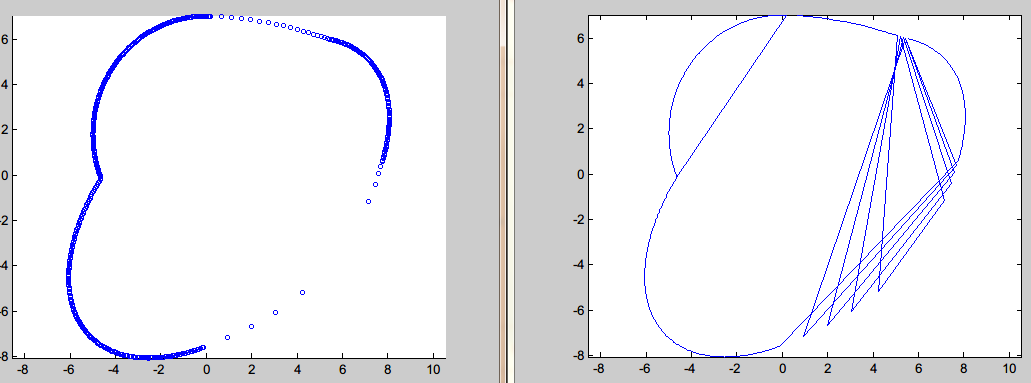
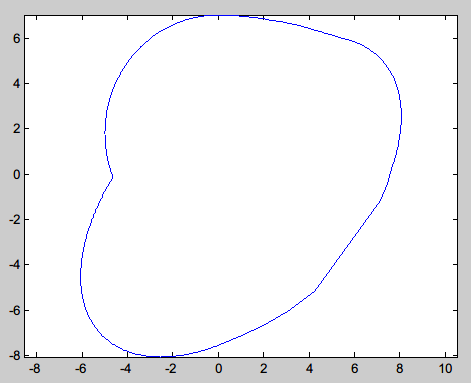
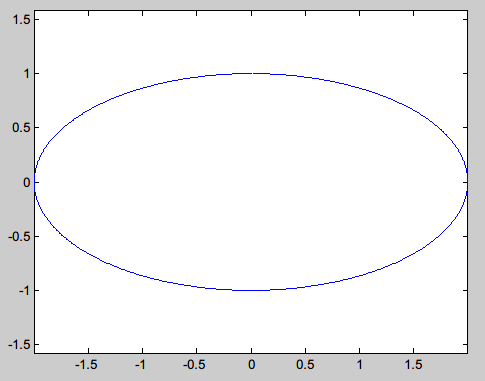
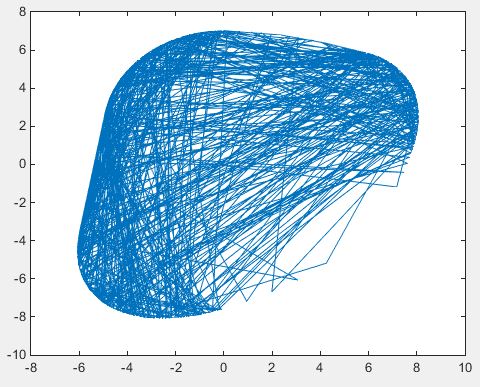
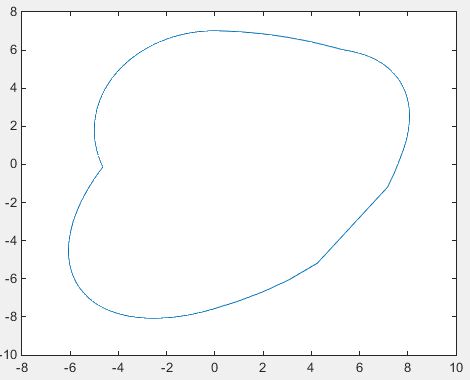
I have a series of discrete point on a plane, However, their order is scattered. Here is an instance:

To connect them with a smooth curve, I wrote a findSmoothBoundary() to achieve the smooth boundary.

Code

    function findSmoothBoundary(boundaryPointSet)
        %initialize the current point
        currentP = boundaryPointSet(1,:);
        
        %Create a space smoothPointsSet  to store the point
        smoothPointsSet = NaN*ones(length(boundaryPointSet),2);
        %delete the current point from the boundaryPointSet
        boundaryPointSet(1,:) = [];
        ptsNum = 1; %record the number of smoothPointsSet
        
        smoothPointsSet(ptsNum,:) = currentP;

        while ~isempty(boundaryPointSet)
            %ultilize the built-in knnsearch() to 
            %achieve the nearest point of current point
            nearestPidx = knnsearch(boundaryPointSet,currentP);
            currentP = boundaryPointSet(nearestPidx,:);
            ptsNum = ptsNum + 1;
            smoothPointsSet(ptsNum,:) = currentP;
            %delete the nearest point from boundaryPointSet
            boundaryPointSet(nearestPidx,:) = [];
        end
        %visualize the smooth boundary
        plot(smoothPointsSet(:,1),smoothPointsSet(:,2))
        axis equal
    end

Although findSmoothBoundary() can find the smooth boundary rightly, but its efficiency is much lower ( About the data, please see here)

---

So I would like to know:

• How to find the discrete point order effieciently?

Data

theta = linspace(0,2*pi,1000)';
boundaryPointSet= [2*sin(theta),cos(theta)];

tic;
findSmoothBoundary(boundaryPointSet)
toc;

%Elapsed time is 4.570719 seconds.

Tropho

How weird can your shape be? Can I suppose that the center of mass is included inside it? (If yes I have an answer with a computational time of approx. 0.2s with your data) – Cool

@Cool This boundary came from a serie of sections. Like this – Tropho

Answer 1

This answer is not perfect because I'll have to make a few hypothesis in order for it to work. However, for a vast majority of cases, it should works as intended. Moreover, from the link you gave in the comments, I think these hypothesis are at least weak, if not verified by definition :

1. The point form a single connected region

2. The center of mass of your points lies in the convex hull of those points

---

If these hypothesis are respected, you can do the following (Full code available at the end):

Step 1 : Calculate the center of mass of your points

Means=mean(boundaryPointSet);

Step 2 : Change variables to set the origin to the center of mass

boundaryPointSet(:,1)=boundaryPointSet(:,1)-Means(1);
boundaryPointSet(:,2)=boundaryPointSet(:,2)-Means(2);

Step3 : Convert coordinates to polar

[Angles,Radius]=cart2pol(boundaryPointSet(:,1),boundaryPointSet(:,2));

Step4 : Sort the Angle and use this sorting to sort the Radius

[newAngles,ids]=sort(Angles);
newRadius=Radius(ids);

Step5 : Go back to cartesian coordinates and re-add the coordinates of the center of mass:

[X,Y]=pol2cart(newAngles,newRadius);
X=X+Means(1);
Y=Y+means(2);

---

Full Code

%%% Find smooth boundary
fid=fopen('SmoothBoundary.txt');
A=textscan(fid,'%f %f','delimiter',',');

boundaryPointSet=cell2mat(A);

boundaryPointSet(any(isnan(boundaryPointSet),2),:)=[];

idx=randperm(size(boundaryPointSet,1));

boundaryPointSet=boundaryPointSet(idx,:);

tic

plot(boundaryPointSet(:,1),boundaryPointSet(:,2))

%% Find mean value of all parameters

Means=mean(boundaryPointSet);

%% Center values around Mean point

boundaryPointSet(:,1)=boundaryPointSet(:,1)-Means(1);
boundaryPointSet(:,2)=boundaryPointSet(:,2)-Means(2);

%% Get polar coordinates of your points

[Angles,Radius]=cart2pol(boundaryPointSet(:,1),boundaryPointSet(:,2));

[newAngles,ids]=sort(Angles);
newRadius=Radius(ids);

[X,Y]=pol2cart(newAngles,newRadius);
X=X+Means(1);
Y=Y+means(2);    
toc

figure

plot(X,Y);

Note : As your values are already sorted in your input file, I had to mess it up a bit by permutating them

Outputs :

Boundary

Elapsed time is 0.131808 seconds.

Messed Input :

Output :

Cool

Thanks a bunch. About the hypothesis 1, it holds. I will test your idea with other case tommorow:) Anyway, it's very nice to convert a boundary conection problem to a coordinates to polar. Here is also a solution with the bult-in ListCurvePathPlot of Mathematica. – Tropho

I see you accepted the answer @ShutaoTANG , does it work well for all your test cases? – Cool

Yes, @BillBokeey, I have tested your idea for many cases, like this, it works well.:) – Tropho