How to quickly get a feasible solution to a linear program in Python?

Question

Goal: Compute the intersection of two convex polytopes.

I am using scipy.spatial.HalfspaceIntersection to do this. The following image shows the resultant intersection: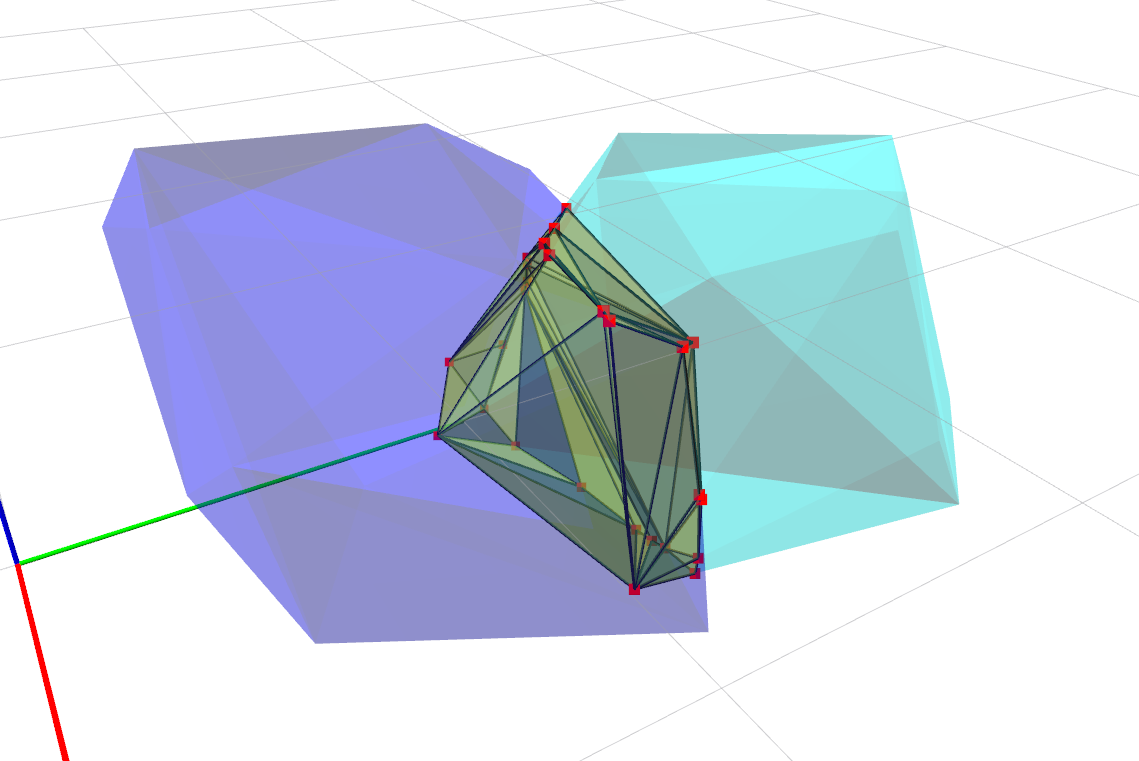

My problem: Determine an initial feasible point.

You see, the current Python implementation of scipy.spatial.HalfspaceIntersection requires an interior_point to be passed as an argument.

interior_point : ndarray of floats, shape (ndim,)
Point clearly inside the region defined by halfspaces. Also called a feasible point, it can be obtained by linear programming.

Now, at the moment, I am manually supplying the feasible point because I was just drafting a prototype to experiment with HalfspaceIntersection. But now I have reached a point where I do not want to manually specify it.

SciPy's optimization module scipy.optimize.linprog implements two general Linear Programming (LP) solvers: simplex, and interior-point. However, they seem to require a cost function. [1]

Since I want to spend the least amount of processing time as possible computing this feasible point, I was wondering how I can run any of these LP methods without a cost function, i.e., only run until the solution has reached a feasible status.

Questions:

1. Is scipy.optimize.linprog the right way to go for computing this feasible interior point?

2. If yes, how can I use either simplex or interior-point without a cost function?

3. Why does scipy.spatial.HalfspaceIntersection require an interior point to be passed as an argument in the first place? To the best of my understanding, an intersection of halfspaces is the removal of the redundant inequalities of a given set of inequalities. Why is a feasible point required for this?

Lawhorn

Zero is a cost function – Ambi

It seems that you're interested in the vertex enumeration problem. Take a look at the first pages of Some Algorithmic Problems in Polytope Theory. If you need an exact vertex, then consider using rational numbers (rather than floats). Take a look at this CGAL package. – Kolva

Answer 1

You can specify a constant cost function, like for example 0.

Here is an example:

%pylab
from scipy.optimize import linprog
A = array([[1] + 9 * [0], 9 * [0] + [1]])
b = array([1, 1])

Measuring the performance of this approach reveals that it is very efficient:

%time
res = linprog(c=zeros(A.shape[1]), A_eq=A, b_eq=b)

Output:

CPU times: user 5 µs, sys: 1 µs, total: 6 µs
Wall time: 11 µs

Moreover, according to res.nit, we were done after only 2 iterations.

The result res.x is correct:

array([ 1.,  0.,  0.,  0.,  0.,  0.,  0.,  0.,  0.,  1.])

Note that the simplex algorithm is designed to find the vertices of the polyhedron defined by the linear constraints. To my understanding, interior point-based methods do not have such a preference, although I'm not familar with the implementation behind scipy's linprog. Hence, since your requirement is that the point is "clearly inside the region defined by halfspaces", I suggest either one of the following:

• Either, pass method='interior-point' to linprog.
• Or, compute different vertices and exploit that the polyhedron is convex:
  1. Add some noise to the constant objective function (e.g., via np.random.randn)
  2. Solve multiple instances of the noise-augmented LP by varying the noise seed (np.random.seed).
  3. Finally, use the mean of your solution as the final interior point "clearly inside the region".

Since it is not clear, how large the margin of your interior point needs to be, I would expect that the second approach (noise-augmented LP) is more robust.

Padraig

Using zero as a cost function to find the feasible point causes this issue upon execution of HalfspaceIntersection(): scipy.spatial.qhull.QhullError: QH6023 qhull input error: feasible point is not clearly inside halfspace. I have ran it multiple times and it always happens: the solution lies either along an edge or in a vertex of the convex set. – Lawhorn

This lies in the nature of this approach: The solution to an LP is always a vertex or an edge. If the solution to your optimization is neither a vertex nor an edge of the polyherdron specified by the linear constraints, then your objective function is non-linear, and hence your optimization problem is not an LP. The only exception here are constant objectives, but still, many solvers will yield the corners (or edges) because they are easier to find. Have you tried passing method='interior-point'? – Padraig

If passing method='interior-point' does not help, you might also want to try (i) adding a bit noise to the constant objective function (e.g., via np.random.randn), (ii) solve multiple instances of the noise-augmented LP by varying the noise seed (np.random.seed), and (iii) finally use the mean of your solution as the final interior point, which you are looking for. This is supposed to work, because the polyhedron defined by linear equalities/inequalities is convex. – Padraig

Yes, I am aware that the nature of the LP involves this, and that a result close to the boundary still is, obviously, a feasible solution. Actually, what I am puzzled about is the reason why the HalfspaceIntersection requires this feasible point; and what does it mean to be "clearly inside the halfspace" --- I mean, how far from the boundaries is "clearly inside"... Anyway, I have switched to method='interior-point' and it solves the problem!! Any intuition why? Thank you very much! – Lawhorn

The simplex algorithm is designed to find the vertices of the polyhedron. To my understanding, interior point-based methods do not have such a preference, although I'm not familar with the implementation behind scipy's linprog. However, in accordance to what you have pointed out, it is not clear, how large the margin of the solution will be or is required to be. Hence, the second approach (noise-augmented LP) might be more robust. – Padraig

I have marked your answer as the accepted one. I think it would be beneficial for future readers to mention the suggestion for switching to interior-point method in your answer, rather than leave it only in these comments. Would appreciate it if you could add it! Thank you again. – Lawhorn