I created some data from two superposed normal distributions and then applied sklearn.neighbors.KernelDensity and scipy.stats.gaussian_kde to estimate the density function. However, using the same bandwith (1.0) and the same kernel, both methods produce a different outcome. Can someone explain me the reason for this? Thanks for help.
Below you can find the code to reproduce the issue:
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import gaussian_kde
import seaborn as sns
from sklearn.neighbors import KernelDensity
n = 10000
dist_frac = 0.1
x1 = np.random.normal(-5,2,int(n*dist_frac))
x2 = np.random.normal(5,3,int(n*(1-dist_frac)))
x = np.concatenate((x1,x2))
np.random.shuffle(x)
eval_points = np.linspace(np.min(x), np.max(x))
kde_sk = KernelDensity(bandwidth=1.0, kernel='gaussian')
kde_sk.fit(x.reshape([-1,1]))
y_sk = np.exp(kde_sk.score_samples(eval_points.reshape(-1,1)))
kde_sp = gaussian_kde(x, bw_method=1.0)
y_sp = kde_sp.pdf(eval_points)
sns.kdeplot(x)
plt.plot(eval_points, y_sk)
plt.plot(eval_points, y_sp)
plt.legend(['seaborn','scikit','scipy'])
If I change the scipy bandwith to 0.25, the result of both methods look approximately the same.

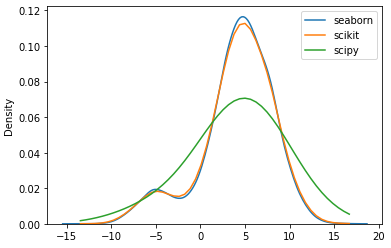
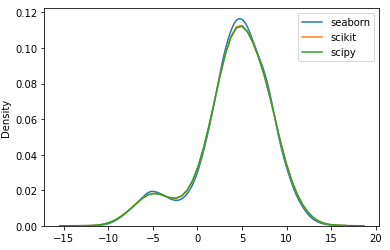
seabornusesscipy.stats.gaussian_kde(bw_method='scott', ...), which is why your results match. – Azzieb