I am working on implementing a voxel octree raycaster, and the only thing left is rearranging the data to populate the leaf level of the octree, so that the data then can be averaged to build the lower levels of the tree.
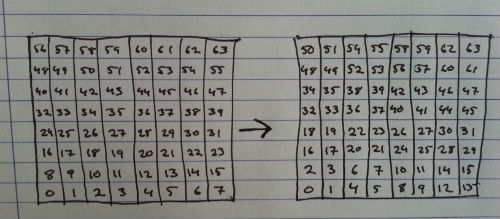
I'm thinking in 2D (quadtree) initially for convenience. I have the data ordered like in the left in the drawing, and I am currently able to rearrange it like to the right. Example is 8x8.
However, I realized that I need to order the data in node order, like in the drawing below:
In other words, I want to go from an array where the data correspond to indices like this:
[0 1 2 3 4 5 6 7 8 9 ... 63]
to an array that would have the data in this order:
[0 1 4 5 16 17 20 21 2 3 ... 63]
for an 8x8 quadtree example.
I can't figure out how to do it. My main problem is dealing with an arbitrary tree size. I could probably hard-code a set of nested loops if I knew the size beforehand, but that it obviously not a great or elegant solution. I'm thinking there might be a recursive way achieve it.
This it what my quick and dirty sketch for sorting the data in the way described in picture one. It basically works by keeping track of four positions in the original data, and then stepping these forward as the new array gets filled. As far as I have been able to tell, this works fine but is not extendable to my needs:
int w = 8;
int[] before = new int[w*w*w];
int[] after = new int[w*w*w];
for (int i=0; i<w*w*w; i++) {
before[i] = i;
}
int toFill = 0;
int front = 0;
int back = w;
int frontZ = w*w;
int backZ = w*w + w;
do {
for (int i=0; i<w/2; i++) {
for (int j=0; j<w/2; j++) {
after[toFill++] = front++;
after[toFill++] = front++;
after[toFill++] = back++;
after[toFill++] = back++;
after[toFill++] = frontZ++;
after[toFill++] = frontZ++;
after[toFill++] = backZ++;
after[toFill++] = backZ++;
}
front += w;
back += w;
frontZ += w;
backZ += w;
}
front += w*w;
back += w*w;
frontZ += w*w;
backZ += w*w;
} while (toFill < w*w*w);
for (int i=0; i<w*w*w; i++) {
println("after " + i + " " + after[i]);
}