How to Generate a Homogeneous Poisson Point Process in a circle?

Question

I would like to generate N points in a circle C of center (0,0) and of radius R=200. The points follow Poisson distribution. In other words, I would like to generate N homogeneous Poisson point process (HPPP) inside C.

I found this paper Generating Homogeneous Poisson Processes . In Section 2 there is exactly what I want. Specifically, in page 4, Algorithm 3 generates the points HPPP inside C.

I implemented this code in Python as follow:

""" Main Codes """    
import matplotlib.pyplot as plt
import numpy as np


lamb = 0.0005 # the rate
pi = np.pi # pi = 3.14...
r = 200 # the radius of the circle C
mean = lamb * pi * r ** 2 # the mean of the Poisson random variable n
n = np.random.poisson(mean) # the Poisson random variable (i.e., the number of points inside C)
u_1 = np.random.uniform(0.0, 1.0, n) # generate n uniformly distributed points 
radii = np.zeros(n) # the radial coordinate of the points
for i in range(n):
    radii[i] = r * (np.sqrt(u_1[i]))
u_2 = np.random.uniform(0.0, 1.0, n) # generate another n uniformly distributed points 
angle = np.zeros(n) # the angular coordinate of the points
for i in range(n):
    angle[i] = 2 * pi * u_2[i]

""" Plots """
fig = plt.gcf()
ax = fig.gca()
plt.xlim(-300, 300)
plt.ylim(-300, 300)
circ = plt.Circle((0, 0), radius=200, color='r', linewidth=2, fill=False)
plt.polar(angle, radii, 'bo')
ax.add_artist(circ)
plt.show()

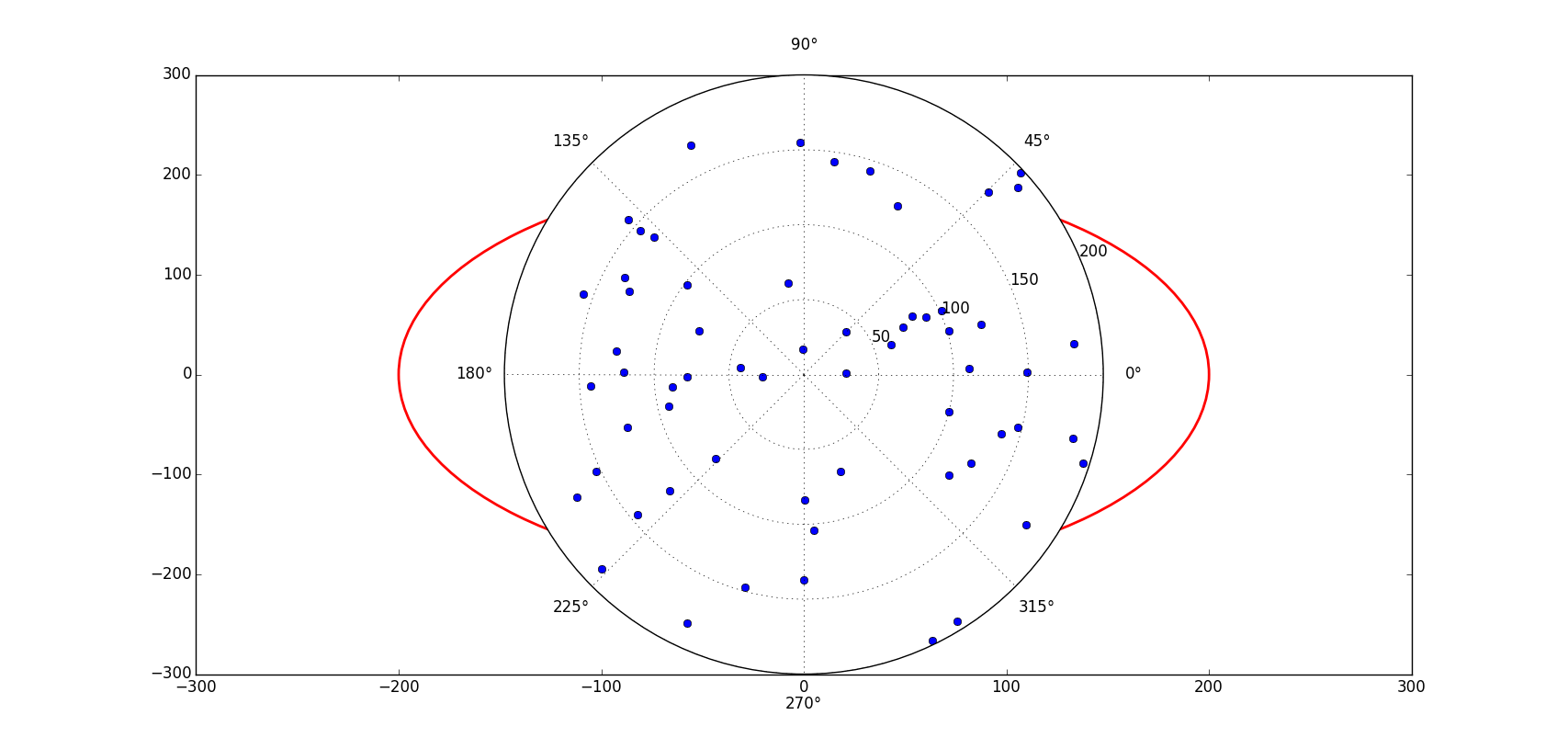
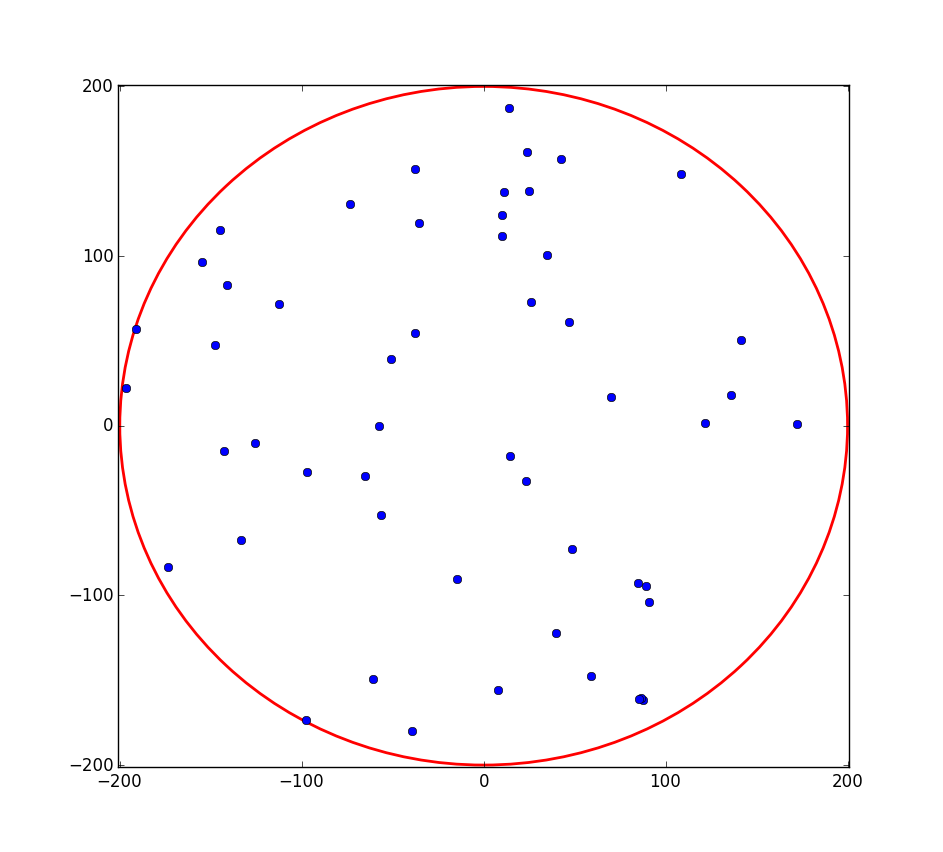
First, I cannot see the points inside the circle. Second, I don't know why the points do not generate inside the circle properly. Is there a problem in my code?

The output is given below: The circle C is in red.

Sensual

Answer 1

I found the answer. I just convert the polar coordinates to the Cartesian coordinates and then I plot with plt.plot() not with plt.polar().

# Cartesian Coordinates
x = np.zeros(n)
y = np.zeros(n)
for i in range(n):
    x[i] = radii[i] * np.cos(angle[i])
    y[i] = radii[i] * np.sin(angle[i])

plt.plot(x,y,'bo')

So I get the desired output.

Sensual

Answer 2

A few years late, but I wrote about this problem a few months ago; see this post.

For future readers, here's my code:

import numpy as np
import scipy.stats
import matplotlib.pyplot as plt

#Simulation window parameters
r=1;
xx0=0; yy0=0; #centre of disk

areaTotal=np.pi*r**2; #area of disk

#Point process parameters
lambda0=100; #intensity (ie mean density) of the Poisson process

#Simulate Poisson point process
numbPoints = scipy.stats.poisson( lambda0*areaTotal ).rvs()#Poisson number of points
theta = 2*np.pi*scipy.stats.uniform.rvs(0,1,((numbPoints,1)))#angular coordinates of Poisson points
rho = r*np.sqrt(scipy.stats.uniform.rvs(0,1,((numbPoints,1))))#radial coordinates of Poisson points

#Convert from polar to Cartesian coordinates
xx = rho * np.cos(theta)
yy = rho * np.sin(theta)

#Shift centre of disk to (xx0,yy0) 
xx=xx+xx0; yy=yy+yy0;

#Plotting
plt.scatter(xx,yy, edgecolor='b', facecolor='none', alpha=0.5 )
plt.xlabel("x"); plt.ylabel("y")
plt.axis('equal')

A sample: A realization of a Poisson point process on a disk

Lyontine