Signal fitting models in Python

Question

I have a dataset shared in the following link:

https://drive.google.com/open?id=0B2Iv8dfU4fTUSV8wMmUwVGMyRE0

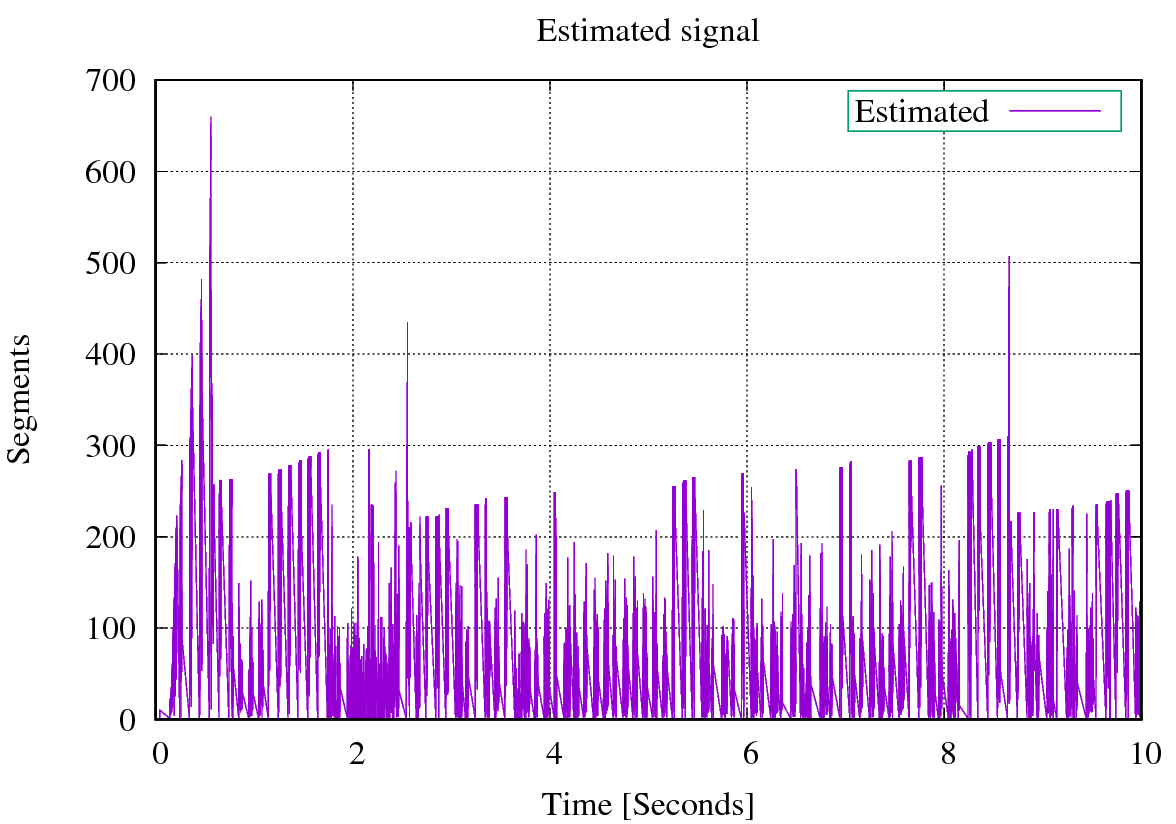
A simple plot of the estimated_data.csv file generates the following plot.

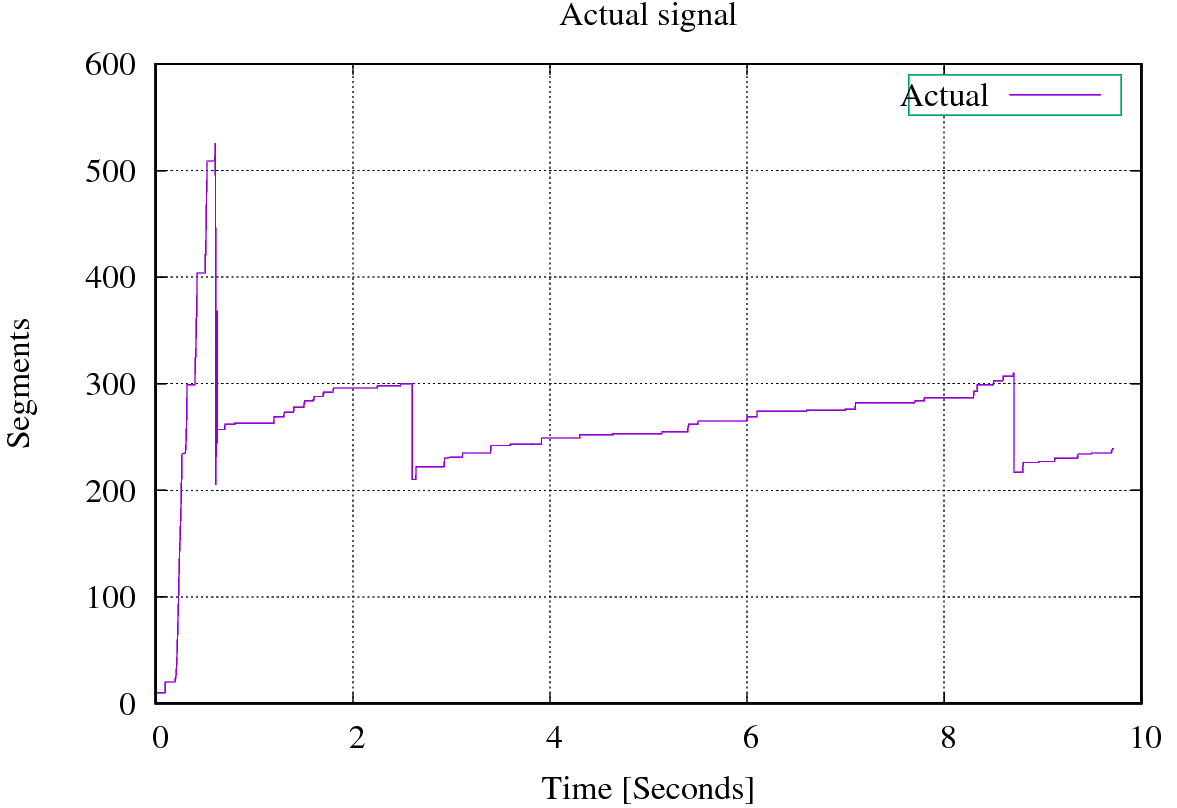
and a simple plot of actual_data.csv (which is my ground truth) generates the following plot

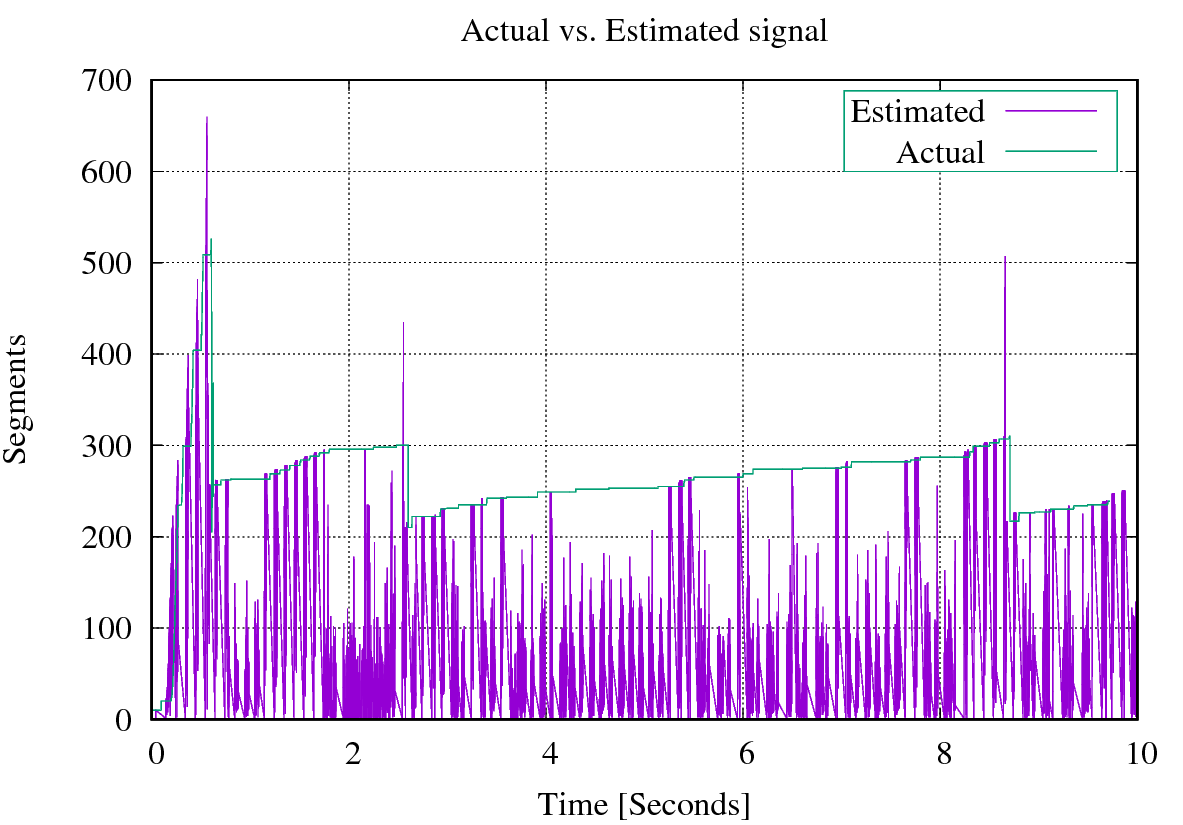
When we plot both the actual and estimated signals together, this is what we got

I wanted to find the closest pattern of the estimated and actual signals. I have tried to find the closest pattern using pandas.rolling_max() by loading the data into a DataFrame and calculate the rolling max and then turn around the whole series and to calculate the windows backwards. Hereunder is my Python script.

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
plt.ion()

df = pd.read_csv('estimated.csv', names=('x','y'))
df['rolling_max'] = df['y'].rolling(8500).max()
df['rolling_max_backwards'] = df['y'][::-1].rolling(850).max()
df.rolling_max.fillna(df.rolling_max_backwards, inplace=True)
plt.figure()
plt.plot(df['x'], df['rolling_max'], label = 'rolling')

plt.legend()
plt.title('Pattern')
plt.xlim(0,10)
plt.ylim(0,700)
plt.xlabel('Time [Seconds]')
plt.ylabel('Segments')
plt.grid()
plt.show(block=True)

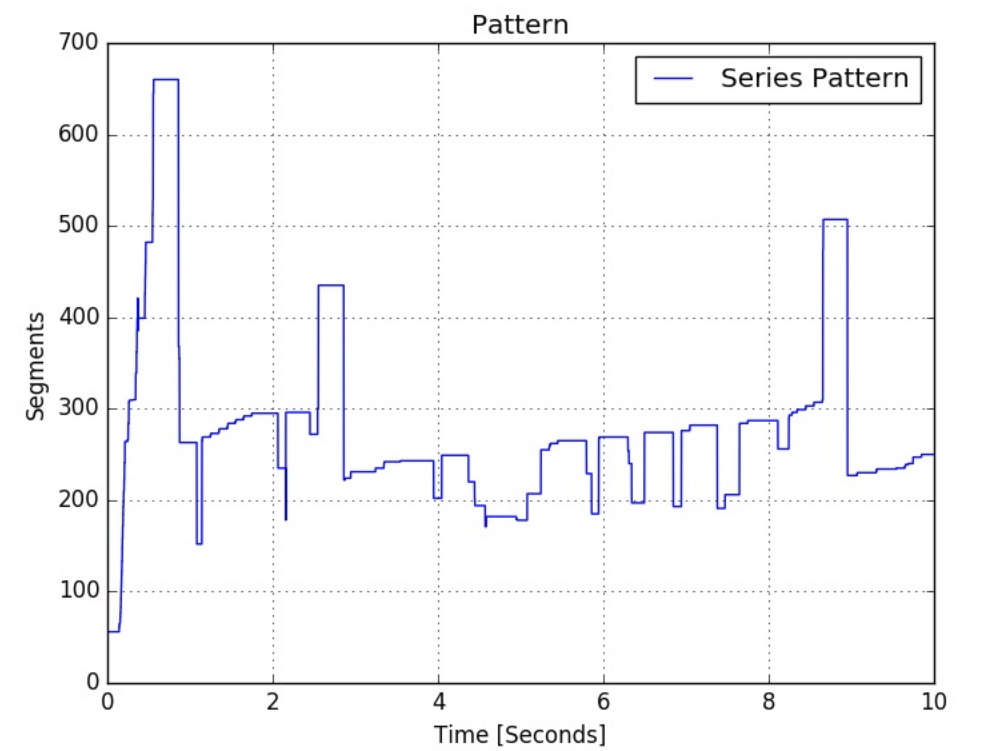
which finally generates the following pattern.

However, I don't feel this pattern is close enough when I compare it with my ground truth (the plot of actual_data.csv). How can we apply filtering models like Kalman Filter to find a pattern of such a signal?

Marciemarcile

Use this example as a roadmap. scipy-cookbook.readthedocs.io/items/KalmanFiltering.html – Folberth

Answer 1

A Kalman Filter is useful for input data which has the true mean value with Gaussian noise added. You measure or otherwise know the variance of the random noise and supply that to the algorithm as the measurement noise. Your input data (which you call "estimated signal") is does not have (on average) the value of your actual signal. It appears to have an error which causes it to measure near zero very often, and rarely higher than the actual value. It only appears to exceed the actual value as a warning that there is about to be a sharp drop in the actual value.

In a case like this, a Kalman filter is unlikely to help you, because its assumptions about the input data are strongly violated by this dataset. Your best bet would be to improve your input data (in this case, for example, the error could be due to a flaw in a sensor). If that's not possible, your own intuition about the data (taking a rolling maximum) is more consistent with the behavior than a KF could be.

Westerman