Linear regression to fit a power-law

Question

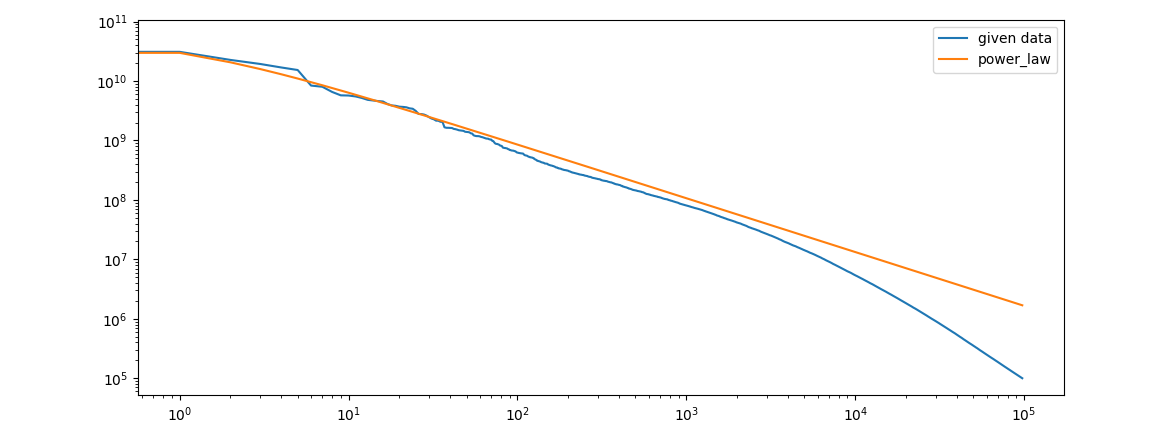
I have two data sets index_list and frequency_list which I plot in a loglog plot by plt.loglog(index_list, freq_list). Now I'm trying to fit a power law a*x^(-b) with linear regression. I expect the curve to follow the initial curve closely but the following code seems to output a similar curve but mirrored on the y-axis. I suspect I am using curve_fit badly.

why is this curve mirrored on the x-axis and how I can get it to properly fit my inital curve?

Using this data

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

f = open ("input.txt", "r")
index_list = []
freq_list = []
index = 0
for line in f:
    split_line = line.split()
    freq_list.append(int(split_line[1]))
    index_list.append(index)
    index += 1

plt.loglog(index_list, freq_list)
def power_law(x, a, b):
    return a * np.power(x, -b)

popt, pcov = curve_fit(power_law, index_list, freq_list)
plt.plot(index_list,  power_law(freq_list, *popt))
plt.show()

Public

Yes, that unfortunately only results in a y=x line – Public

@JohanC I have edited the post to include sample data. – Public

linearize y = a * x^b to log(y) = log(a) + b*log(x) and find solution with scipy.ptimize.leastsq - see xample in scipy-cookbook – Tomekatomes

Answer 1

The code below made the following changes:

• For the scipy functions to work, it is best that both index_list and freq_list are numpy arrays, not Python lists. Also, for the power not to overflow too rapidly, these arrays should be of float type (not of int).
• As 0 to a negative power causes a divide-by-zero problem, it makes sense to start the index_list with 1.
• Due to the powers, also for floats an overflow can be generated. Therefore, it makes sense to add bounds to curve_fit. Especially b should be limited not to cross about 50 (the highest value is about power(100000, b) giving an overflow when be.g. is100). Also setting initial values helps to direct the fitting process (p0=...).
• Drawing a plot with index_list as x and power_law(freq_list, ...) as y would generate a very weird curve. It is necessary that the same x is used for the plot and for the function.

Note that calling plt.loglog() changes both axes of the plot to logarithmic. All subsequent plots on the same axes will continue to use the logarithmic scale.

import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import pandas as pd
import numpy as np

def power_law(x, a, b):
    return a * np.power(x, -b)

df = pd.read_csv("https://norvig.com/google-books-common-words.txt", delim_whitespace=True, header=None)

index_list = df.index.to_numpy(dtype=float) + 1
freq_list = df[1].to_numpy(dtype=float)

plt.loglog(index_list, freq_list, label='given data')

popt, pcov = curve_fit(power_law, index_list, freq_list, p0=[1, 1], bounds=[[1e-3, 1e-3], [1e20, 50]])

plt.plot(index_list, power_law(index_list, *popt), label='power law')
plt.legend()
plt.show()

Ortiz