Sample from a Bayesian network in pomegranate

Question

I constructed a Bayesian network using from_samples() in pomegranate. I'm able to get maximally likely predictions from the model using model.predict(). I wanted to know if there is a way to sample from this Bayesian network conditionally(or unconditionally)? i.e. is there a get random samples from the network and not the maximally likely predictions?

I looked at model.sample(), but it was raising NotImplementedError.

Also if this is not possible to do using pomegranate, what other libraries are great for Bayesian networks in Python?

Refutative

Answer 1

The model.sample() should have been implemented by now if I see the commit history correctly.

You can have a look at PyMC which supports distribution mixtures as well. However, I dont know any other toolbox with a similar factory method like from_samples() in pomogranate.

Danicadanice

the linked commit is for the BayesModel class not the BayesianNetwork class about which the OP is inquiring. see here: github.com/jmschrei/pomegranate/blob/master/pomegranate/… – Catcall

Answer 2

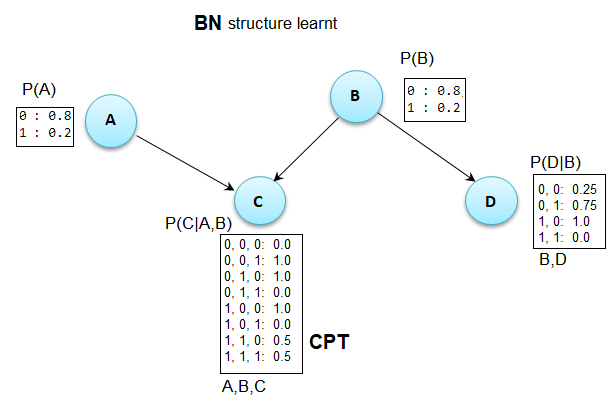
Just to elucidate the above answers with a concrete example, so that it will be helpful for someone, let's start with the following simple dataset (with 4 variables and 5 data points):

import pandas as pd
df = pd.DataFrame({'A':[0,0,0,1,0], 'B':[0,0,1,0,0], 'C':[1,1,0,0,1], 'D':[0,1,0,1,1]})
df.head()

#   A   B   C   D
#0  0   0   1   0
#1  0   0   1   1
#2  0   1   0   0
#3  1   0   0   1
#4  0   0   1   1 

Now let's learn the Bayesian Network structure from the above data using the 'exact' algorithm with pomegranate (uses DP/A* to learn the optimal BN structure), using the following code snippet

import numpy as np
from pomegranate.bayesian_network import *
model = BayesianNetwork.from_samples(df.to_numpy(), state_names=df.columns.values, algorithm='exact')
# model.plot()

The BN structure that is learn is shown in the next figure along with the corresponding CPTs

As can be seen from the above figure, it explains the data exactly. We can compute the log-likelihood of the data with the model as follows:

np.sum(model.log_probability(df.to_numpy()))
# -7.253364813857112

Once the BN structure is learnt, we can sample from the BN as follows:

model.sample()  
# array([[0, 1, 0, 0]], dtype=int64)

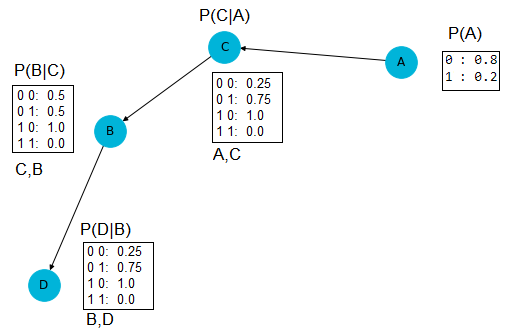
As a side note, if we use algorithm='chow-liu' instead (which finds a tree-like structure with fast approximation), we shall obtain the following BN:

The log-likelihood of the data this time is

np.sum(model.log_probability(df.to_numpy()))
# -8.386987635761297

which indicates the algorithm exact finds better estimate.

Nordrheinwestfalen

How did you print CPTs in the figures above ? model.plot() shows only nodes/edges without CPTs. – Revanche

Answer 3

One way to sample from a 'baked' BayesianNetwork is using the predict_proba method. predict_proba returns a list of distributions corresponding to each node for which information was not provided, conditioned on the information that was provided.

e.g. :

bn = BayesianNetwork.from_samples(X)
proba = bn.predict_proba({"1":1,"2":0}) # proba will be an array of dists
samples = np.empty_like(proba)
for i in np.arange(proba.shape[0]):
    for j in np.arange(proba.shape[1]):
        if hasattr(proba[i][j],'sample'):
            samples[i,j] = proba[i][j].sample(10000).mean() #sample and aggregate however you want
        else:
            samples[i,j] = proba[i][j]
pd.Series(samples,index=X.columns) #convert samples to a pandas.Series with column labels as index

Catcall