Matlab Image Baseline (Offset Removal) Correction

Question

I have this plot:

and want to flatten its baseline/reduce offset using Matlab.

Basically like a baseline correction for a spectrum but here I've got a mesh and can't get my head around it how to flatten its baseline when dealing with a matrix? Basically the dot should stay but the surrounding is actually zero. The noise can stay, though.

Here is the image:

I am wondering if something like this works:

        for x=1:1201
        for y=1:1201
             Ibasetest = polyfit(x,y,1);
        end
        end

Simply put do a baseline for each X along Y for Z data. But I can't get it to work. :(

Indurate

How would you proceed with a simple signal? What baseline removal technical would you use? What is your input and what is the expected output? – Growth

Just very basic. The dot in the middle should stay but I want to remove the offset around it. At the moment its like 10 to 60 offset. This should be pulled down to 0. Simple linear fit should do. Rest I can learn by playing around. – Indurate

Would you happen to be willing to post the input image you used? That might make it easier to play around and test some methods. – Cristinecristiona

Attached :) So basically the dark surrounding should be black. The noise can stay. I just want to remove the offset. Its not a constant offset across (that would be easy) but there's a tilt in the image baseline. – Indurate

Oh, just noticed your comment. I'll try to accommodate the tilt and edit my answer. – Cristinecristiona

@Indurate A few methods I can propose are filtering out the noise first, thresholding the image or doing a sliding/moving window average to estimate the amount of offset to remove for each point (pixel). I'm curious how involved of a method you're looking for. – Cristinecristiona

Thanks @Cristinecristiona I already applied medfilt3(). Thats fine. – Indurate

Answer 1

Note: Another method to attempt may include moving/windowing averages to calculate the local amount to offset by.

Method 1: Discrete Cosine Transform (DC Offset Removal)

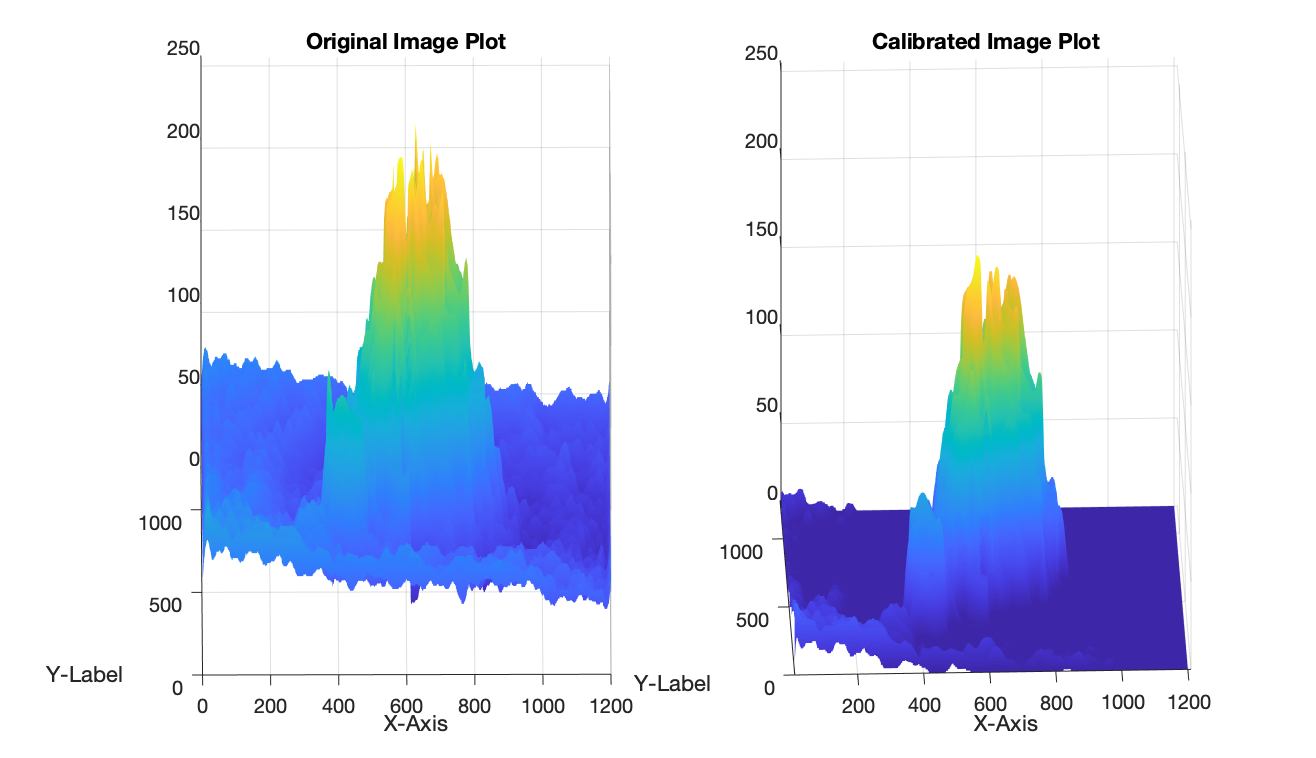
Converts the image into the frequency domain uses the Discrete Fourier Transform (DCT). Removes the DC coefficient in the top-left corner (set to zero) of the matrix and convert it back to the spatial domain using the Inverse Discrete Fourier Transform (IDCT).

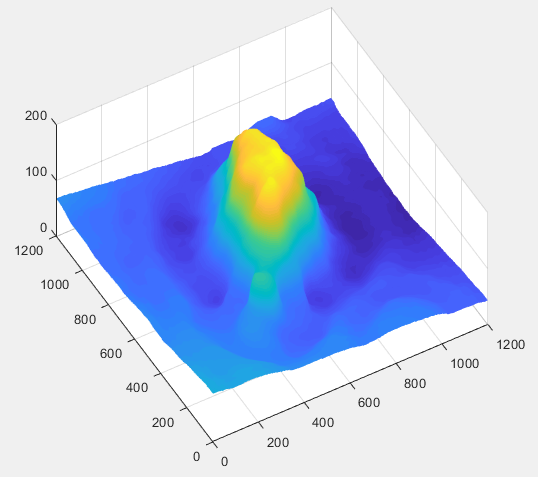
Image = imread("Test_Image.jpg");

%Converting image to greyscale if RGB image%
[Image_Height,Image_Width,Depth] = size(Image);
if(Depth == 3)
Image = rgb2gray(Image);
end

%Removing image offset%    
Discrete_Cosine_Transformed_Image = dct2(Image);
Discrete_Cosine_Transformed_Image(1,1) = 0;
Inverse_Discrete_Cosine_Transformed_Image = idct2(Discrete_Cosine_Transformed_Image);

Calibrated_Image = medfilt2(Inverse_Discrete_Cosine_Transformed_Image,[20 20]);

% Plotting the original and thresholded image%
X_Axes = (1:1:Image_Height);
Y_Axes = (1:1:Image_Width);

subplot(1,2,1); surf(X_Axes,Y_Axes,Image,'EdgeColor','none');
title("Original Image Plot");
xlabel('X-Axis'); ylabel('Y-Label');
zlim([0 255]);

subplot(1,2,2); surf(X_Axes,Y_Axes,uint8(Calibrated_Image),'EdgeColor','none');
title("Calibrated Image Plot");
xlabel('X-Axis'); ylabel('Y-Label');
zlim([0 255]);

Key Discrete Cosine Transform (DCT) Filtering Code Lines

%Removing image offset%    
Discrete_Cosine_Transformed_Image = dct2(Image);
Discrete_Cosine_Transformed_Image(1,1) = 0;
Inverse_Discrete_Cosine_Transformed_Image = idct2(Discrete_Cosine_Transformed_Image)

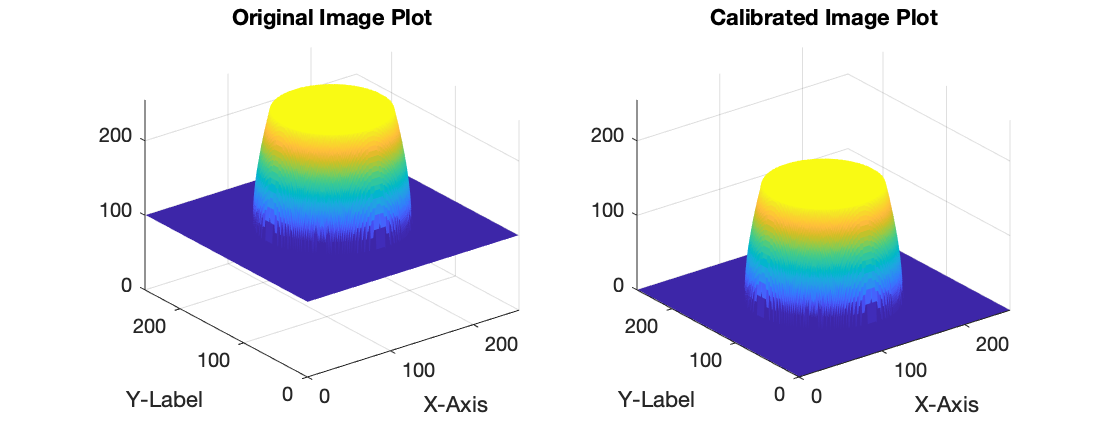
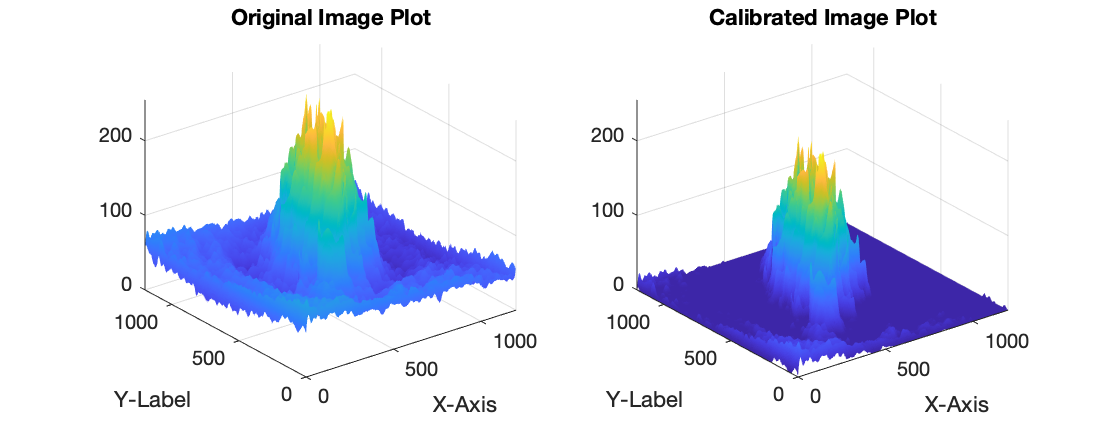
Method 2: Standard Uniform Offset (no-tilt accommodation)

Uses a constant value and subtracts that across the whole image matrix.

Test Image 1: Using Lowest Intensity to Calculate Offset

Test Image 2: Using Average/Mean to Calculate Offset

Image = imread("Circular_Image.png");

%Converting image to greyscale if RGB image%
[Image_Height,Image_Width,Depth] = size(Image);
if(Depth == 3)
Image = rgb2gray(Image);
end

   %Removing image offset%
Lowest_Intensity_Value = min(Image,[],'all');
Average = mean(Image,'all');
Calibrated_Image = Image - Average;

% Plotting the original and thresholded image%
X_Axes = (1:1:Image_Height);
Y_Axes = (1:1:Image_Width);

subplot(1,2,1); surf(X_Axes,Y_Axes,Image,'EdgeColor','none');
title("Original Image Plot");
xlabel('X-Axis'); ylabel('Y-Label');
zlim([0 255]);

subplot(1,2,2); surf(X_Axes,Y_Axes,Calibrated_Image,'EdgeColor','none');
title("Calibrated Image Plot");
xlabel('X-Axis'); ylabel('Y-Label');
zlim([0 255]);

Using MATLAB version: R2019b

Cristinecristiona

Oh well. I was after a simple function removing the offset/baseline, even as linear regression. Super simple with line graphs but I cant get it done with 2D. – Indurate

@Indurate Feel the same way on this one. I'll let you know if I find anything more concise and simple. – Cristinecristiona

I tried with a loop that slices each X, Y and does a baseline subtraction matrix but didn't really work. % for x=1:1201 % for y=1:1201 % Ibasetest = polyfit(x,y,1); % end % end % – Indurate

That's an interesting idea I'll have to look into. – Cristinecristiona

I thought it gives a linear baseline for each X line along the Y direction. Basically Y = 1200 graphs having a line. Then this should be done for each Y in X direction, right? Then subtracting this from the actual image. – Indurate

I forgot to mention this should be a simple method because I am processing 100 per second and more complex code is bad^^ – Indurate

That logic is correct. Hmm, not sure how well it would work. Might have a try myself. The biggest bottleneck I found is median filtering. The DCT portion is decently quick and 3 lines of code if that suffices. – Cristinecristiona

Another idea: Smooth out entire plane across 300 pixel and use resulting 'image' as baseline? – Indurate

That may work. But the speed may suffer depending on the smoothing method used. – Cristinecristiona