For very small collections the difference is going to be negligible. At the low end of your range (500k items) you will start to see a difference if you're doing lots of lookups. A binary search is going to be O(log n), whereas a hash lookup will be O(1), amortized. That's not the same as truly constant, but you would still have to have a pretty terrible hash function to get worse performance than a binary search.
(When I say "terrible hash", I mean something like:
hashCode()
{
return 0;
}
Yeah, it's blazing fast itself, but causes your hash map to become a linked list.)
ialiashkevich wrote some C# code using an array and a Dictionary to compare the two methods, but it used Long values for keys. I wanted to test something that would actually execute a hash function during the lookup, so I modified that code. I changed it to use String values, and I refactored the populate and lookup sections into their own methods so it's easier to see in a profiler. I also left in the code that used Long values, just as a point of comparison. Finally, I got rid of the custom binary search function and used the one in the Array class.
Here's that code:
class Program
{
private const long capacity = 10_000_000;
private static void Main(string[] args)
{
testLongValues();
Console.WriteLine();
testStringValues();
Console.ReadLine();
}
private static void testStringValues()
{
Dictionary<String, String> dict = new Dictionary<String, String>();
String[] arr = new String[capacity];
Stopwatch stopwatch = new Stopwatch();
Console.WriteLine("" + capacity + " String values...");
stopwatch.Start();
populateStringArray(arr);
stopwatch.Stop();
Console.WriteLine("Populate String Array: " + stopwatch.ElapsedMilliseconds);
stopwatch.Reset();
stopwatch.Start();
populateStringDictionary(dict, arr);
stopwatch.Stop();
Console.WriteLine("Populate String Dictionary: " + stopwatch.ElapsedMilliseconds);
stopwatch.Reset();
stopwatch.Start();
Array.Sort(arr);
stopwatch.Stop();
Console.WriteLine("Sort String Array: " + stopwatch.ElapsedMilliseconds);
stopwatch.Reset();
stopwatch.Start();
searchStringDictionary(dict, arr);
stopwatch.Stop();
Console.WriteLine("Search String Dictionary: " + stopwatch.ElapsedMilliseconds);
stopwatch.Reset();
stopwatch.Start();
searchStringArray(arr);
stopwatch.Stop();
Console.WriteLine("Search String Array: " + stopwatch.ElapsedMilliseconds);
}
/* Populate an array with random values. */
private static void populateStringArray(String[] arr)
{
for (long i = 0; i < capacity; i++)
{
arr[i] = generateRandomString(20) + i; // concatenate i to guarantee uniqueness
}
}
/* Populate a dictionary with values from an array. */
private static void populateStringDictionary(Dictionary<String, String> dict, String[] arr)
{
for (long i = 0; i < capacity; i++)
{
dict.Add(arr[i], arr[i]);
}
}
/* Search a Dictionary for each value in an array. */
private static void searchStringDictionary(Dictionary<String, String> dict, String[] arr)
{
for (long i = 0; i < capacity; i++)
{
String value = dict[arr[i]];
}
}
/* Do a binary search for each value in an array. */
private static void searchStringArray(String[] arr)
{
for (long i = 0; i < capacity; i++)
{
int index = Array.BinarySearch(arr, arr[i]);
}
}
private static void testLongValues()
{
Dictionary<long, long> dict = new Dictionary<long, long>(Int16.MaxValue);
long[] arr = new long[capacity];
Stopwatch stopwatch = new Stopwatch();
Console.WriteLine("" + capacity + " Long values...");
stopwatch.Start();
populateLongDictionary(dict);
stopwatch.Stop();
Console.WriteLine("Populate Long Dictionary: " + stopwatch.ElapsedMilliseconds);
stopwatch.Reset();
stopwatch.Start();
populateLongArray(arr);
stopwatch.Stop();
Console.WriteLine("Populate Long Array: " + stopwatch.ElapsedMilliseconds);
stopwatch.Reset();
stopwatch.Start();
searchLongDictionary(dict);
stopwatch.Stop();
Console.WriteLine("Search Long Dictionary: " + stopwatch.ElapsedMilliseconds);
stopwatch.Reset();
stopwatch.Start();
searchLongArray(arr);
stopwatch.Stop();
Console.WriteLine("Search Long Array: " + stopwatch.ElapsedMilliseconds);
}
/* Populate an array with long values. */
private static void populateLongArray(long[] arr)
{
for (long i = 0; i < capacity; i++)
{
arr[i] = i;
}
}
/* Populate a dictionary with long key/value pairs. */
private static void populateLongDictionary(Dictionary<long, long> dict)
{
for (long i = 0; i < capacity; i++)
{
dict.Add(i, i);
}
}
/* Search a Dictionary for each value in a range. */
private static void searchLongDictionary(Dictionary<long, long> dict)
{
for (long i = 0; i < capacity; i++)
{
long value = dict[i];
}
}
/* Do a binary search for each value in an array. */
private static void searchLongArray(long[] arr)
{
for (long i = 0; i < capacity; i++)
{
int index = Array.BinarySearch(arr, arr[i]);
}
}
/**
* Generate a random string of a given length.
* Implementation from https://mcmap.net/q/22142/-how-can-i-generate-random-alphanumeric-strings
*/
private static String generateRandomString(int length)
{
var chars = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789";
var stringChars = new char[length];
var random = new Random();
for (int i = 0; i < stringChars.Length; i++)
{
stringChars[i] = chars[random.Next(chars.Length)];
}
return new String(stringChars);
}
}
Here are the results with several different sizes of collections. (Times are in milliseconds.)
500000 Long values...
Populate Long Dictionary: 26
Populate Long Array: 2
Search Long Dictionary: 9
Search Long Array: 80
500000 String values...
Populate String Array: 1237
Populate String Dictionary: 46
Sort String Array: 1755
Search String Dictionary: 27
Search String Array: 1569
1000000 Long values...
Populate Long Dictionary: 58
Populate Long Array: 5
Search Long Dictionary: 23
Search Long Array: 136
1000000 String values...
Populate String Array: 2070
Populate String Dictionary: 121
Sort String Array: 3579
Search String Dictionary: 58
Search String Array: 3267
3000000 Long values...
Populate Long Dictionary: 207
Populate Long Array: 14
Search Long Dictionary: 75
Search Long Array: 435
3000000 String values...
Populate String Array: 5553
Populate String Dictionary: 449
Sort String Array: 11695
Search String Dictionary: 194
Search String Array: 10594
10000000 Long values...
Populate Long Dictionary: 521
Populate Long Array: 47
Search Long Dictionary: 202
Search Long Array: 1181
10000000 String values...
Populate String Array: 18119
Populate String Dictionary: 1088
Sort String Array: 28174
Search String Dictionary: 747
Search String Array: 26503
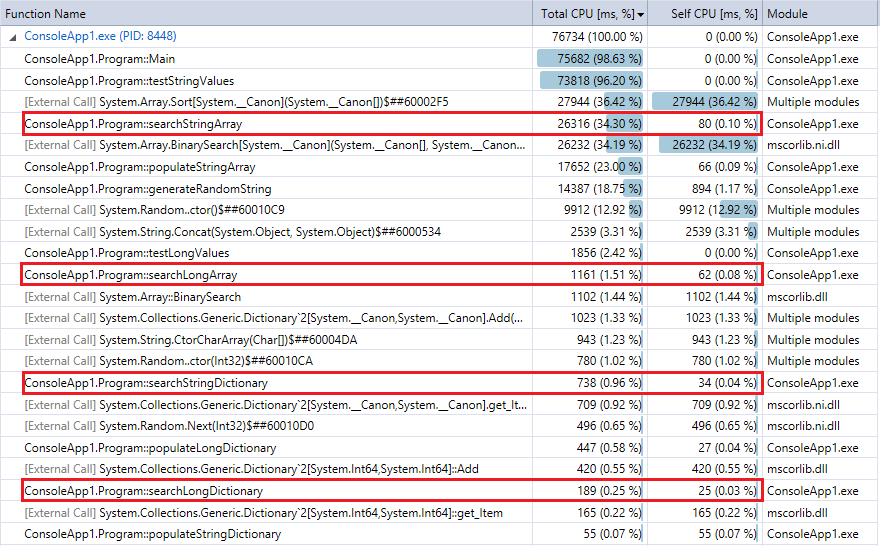
And for comparison, here's the profiler output for the last run of the program (10 million records and lookups). I highlighted the relevant functions. They pretty closely agree with the Stopwatch timing metrics above.
![Profiler output for 10 million records and lookups]()
You can see that the Dictionary lookups are much faster than binary search, and (as expected) the difference is more pronounced the larger the collection. So, if you have a reasonable hashing function (fairly quick with few collisions), a hash lookup should beat binary search for collections in this range.