In my method newminimax499 I have a minimax algorithm that utilizes memoization and alpha beta pruning. The method works normally for 3x3 games, however when I play 4x4 games I get strange, unexpected position choices for the computer. He still never loses, but he doesn't seem to be playing to win. To illustrate the problem here is a scenario from 2 games in 3x3 and 4x4. First here is a scenario from a 3x3 game where the player is X and makes the first move: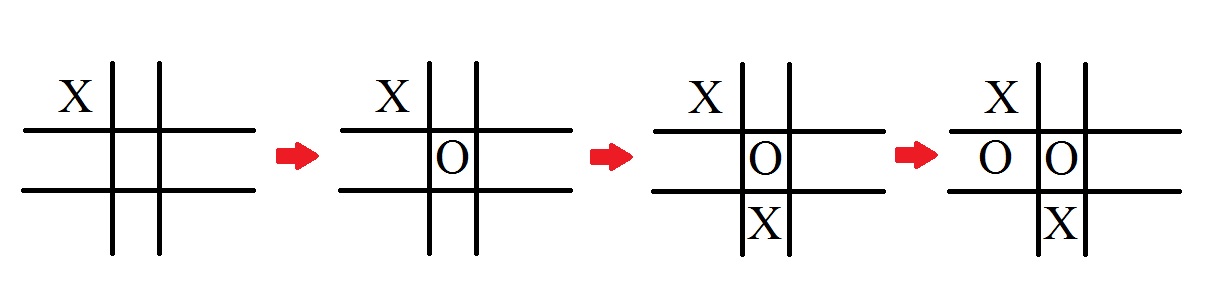
This isn't bad, in fact it's what one would expect the computer to do. Now take a look at a scenario from a 4x4 game. Again O is the computer and X starts:
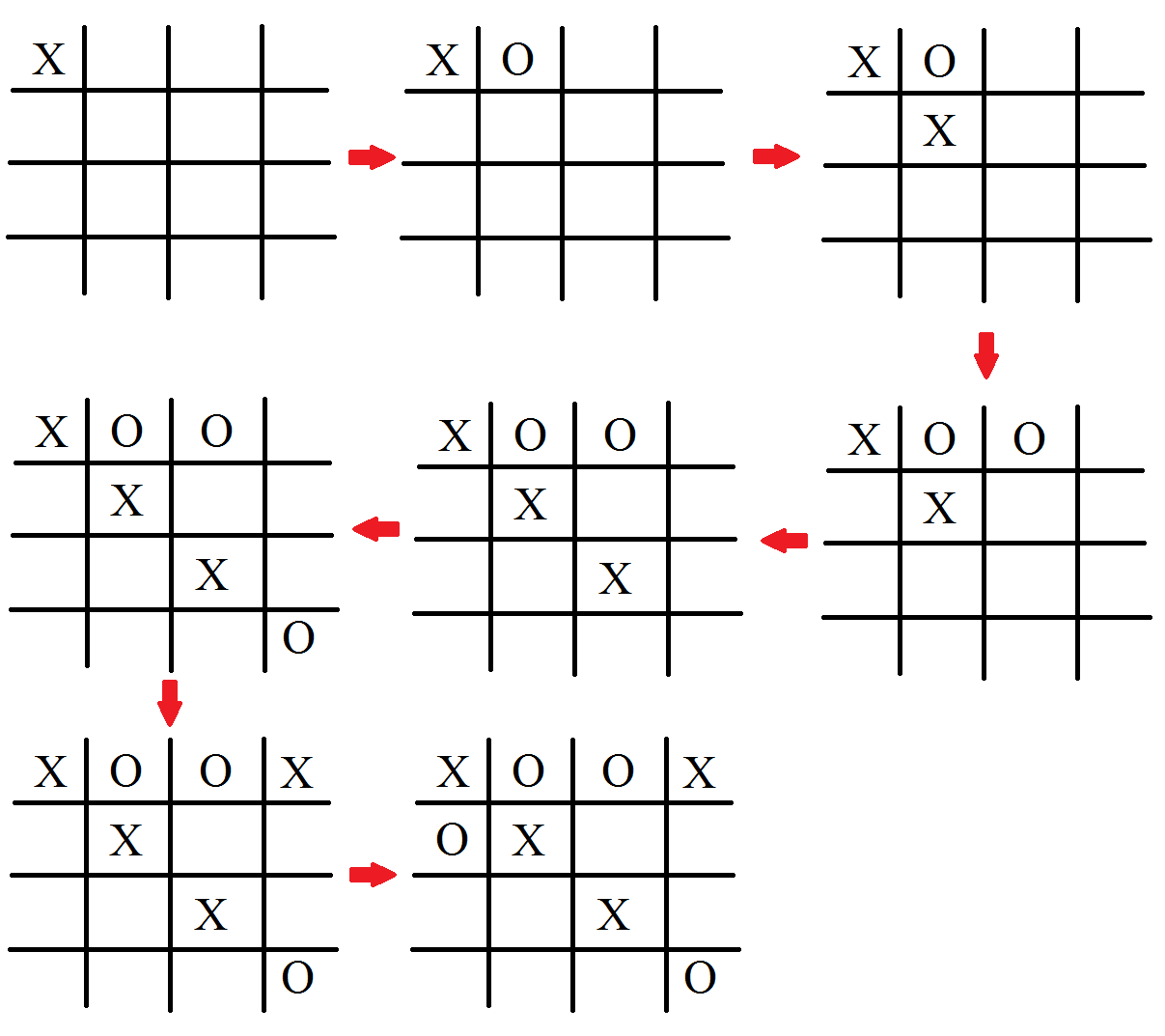
As you can see, the computer is simply placing Os in a systematic order one after the other and only breaking that order to block X when it has a potential win. This is very defensive play, unlike what was seen in the 3x3 game. So why is the method behaving differently for 3x3 and 4x4?
Here is the code:
//This method returns a 2 element int array containing the position of the best possible
//next move and the score it yields. Utilizes memoization and alpha beta
//pruning to achieve better performance.
public int[] newminimax499(int a, int b){
//int bestScore = (turn == 'O') ? +9 : -9; //X is minimizer, O is maximizer
int bestPos=-1;
int alpha= a;
int beta= b;
int currentScore;
//boardShow();
String stateString = "";
for (int i=0; i<state.length; i++)
stateString += state[i];
int[] oldAnswer = oldAnswers.get(stateString);
if (oldAnswer != null)
return oldAnswer;
if(isGameOver()!='N'){
int[] answer = {score(), bestPos};
oldAnswers.put (stateString, answer);
return answer;
}
else{
for(int x:getAvailableMoves()){
if(turn=='X'){ //X is minimizer
setX(x);
//System.out.println(stateID++);
currentScore = newminimax499(alpha, beta)[0];
revert(x);
if(currentScore<beta){
beta=currentScore;
bestPos=x;
}
if(alpha>=beta){
break;
}
}
else { //O is maximizer
setO(x);
//System.out.println(stateID++);
currentScore = newminimax499(alpha, beta)[0];
revert(x);
if(currentScore>alpha){
alpha=currentScore;
bestPos=x;
}
if(alpha>=beta){
break;
}
}
}
}
if(turn=='X'){
int[] answer = {beta, bestPos};
oldAnswers.put (stateString, answer);
return answer;
}
else {
int[] answer = {alpha, bestPos};
oldAnswers.put (stateString, answer);
return answer;
}
}
Following are the other components and complementary methods needed for you guys to run the code. The fields and constructor used in my class State2:
private char [] state; //Actual content of the board
private char turn; //Whose turn it is
private Map<String,int[]> oldAnswers; //Used for memoization. It saves every state along with the score it yielded which allows us to stop exploring the children of a certain node if a similar node's score has been previously calculated. The key is the board state(i.e OX------X for example), the int array is a 2 element array containing the score and position of last placed seed of the state.
private Map<Integer, int []> RowCol; //A mapping of positions from a board represented as a normal array to a board represented as a 2d array. For example: The position 0 maps to 0,0 on a 2d array board, 1 maps to 0,1 and so on.
private static int n; //Size of the board
private static int stateID; //An simple incrementer used to show number of recursive calls in the newminiax49 method.
private static int countX, countO; //Number of placed Xs and Os
private static int lastAdded; //Position of last placed seed
private char [][] DDState; //A 2d array representing the board. Contains the same values as state[]. Used for simplicity in functions that check the state of the board.
public State2(int n){
int a=0;
State2.n=n;
state=new char[n*n];
RowCol=new HashMap<Integer, int []>();
countX=0;
countO=0;
//Initializing the board with empty slots
for(int i = 0; i<state.length; i++){
state[i]='-';
}
//Mapping
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
RowCol.put(a, new int[]{i, j});
a++;
}
}
a=0;
DDState=new char[n][n];
//Initializing the 2d array with the values from state[](empty slots)
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
DDState[i][j]=state[a];
a++;
}
}
oldAnswers = new HashMap<String,int[]>();
}
Complementary methods:
getAvailableMoves, returns an array with the empty slots on the board(i.e. the possible next moves).
public int[] getAvailableMoves(){
int count=0;
int i=0;
for(int j=0; j<state.length; j++){
if(state[j]=='-')
count++;
}
int [] availableSlots = new int[count];
for(int j=0; j<state.length; j++){
if(state[j]=='-')
availableSlots[i++]=j;
}
return availableSlots;
}
isGameOver2(), simply checks the current state of the board for whether the game is over. returns a char 'X', 'O', 'D' and 'N' which stand for X won, O won, Draw, and Not gameover respectively.
public char isGameOver2(){
char turnOpp;
int count;
if(turn=='X'){
count=countO;
turnOpp='O';
}
else {
count=countX;
turnOpp='X';
}
if(count>=n){
for(int i=0; i<n; i++){
if(DDState[i][RowCol.get(lastAdded)[1]]!=turnOpp)
break;
if(i==(n-1)){
return turnOpp;
}
}
//Check row for win
for(int i=0; i<n; i++){
if(DDState[RowCol.get(lastAdded)[0]][i]!=turnOpp)
break;
if(i==(n-1)){
return turnOpp;
}
}
//Check diagonal for win
if(RowCol.get(lastAdded)[0] == RowCol.get(lastAdded)[1]){
//we're on a diagonal
for(int i = 0; i < n; i++){
if(DDState[i][i] != turnOpp)
break;
if(i == n-1){
return turnOpp;
}
}
}
//check anti diagonal
for(int i = 0; i<n; i++){
if(DDState[i][(n-1)-i] != turnOpp)
break;
if(i == n-1){
return turnOpp;
}
}
//check for draw
if((countX+countO)==(n*n))
return 'D';
}
return 'N';
}
boardShow, returns a matrix display of the current state of the board:
public void boardShow(){
if(n==3){
System.out.println(stateID);
for(int i=0; i<=6;i+=3)
System.out.println("["+state[i]+"]"+" ["+state[i+1]+"]"+" ["+state[i+2]+"]");
System.out.println("***********");
}
else {
System.out.println(stateID);
for(int i=0; i<=12;i+=4)
System.out.println("["+state[i]+"]"+" ["+state[i+1]+"]"+" ["+state[i+2]+"]"+" ["+state[i+3]+"]");
System.out.println("***********");
}
}
score, is a simple evaluation function which returns +10 for an O win, -10 for an X win and 0 for a draw:
public int score(){
if(isGameOver2()=='X')
return -10;
else if(isGameOver2()=='O')
return +10;
else
return 0;
}
The seed setters:
//Sets an X at a certain location and updates the turn, countX and lastAdded variables
public void setX(int i){
state[i]='X';
DDState[RowCol.get(i)[0]][RowCol.get(i)[1]]='X';
turn='O';
countX++;
lastAdded=i;
}
//Sets an O at a certain location and updates the turn, countO and lastAdded variables
public void setO(int i){
state[i]='O';
DDState[RowCol.get(i)[0]][RowCol.get(i)[1]]='O';
turn='X';
countO++;
lastAdded=i;
}
Revert, simply reverts a move. For example if an X has been placed in position 0 revert(0) sets a '-' in it's place and updates the variables changed by setX:
public void revert(int i){
state[i]='-';
DDState[RowCol.get(i)[0]][RowCol.get(i)[1]]='-';
if(turn=='X'){
turn = 'O';
countO--;
}
else {
turn = 'X';
countX--;
}
}
How the main method might look like:
public static void main(String[] args) {
State2 s=new State2(4);
int [] results=new int[2];
s.setX(0);
long startTime = System.currentTimeMillis();
results=s.newminimax499(Integer.MIN_VALUE,Integer.MAX_VALUE);
long endTime = System.currentTimeMillis();
System.out.println("Score: "+results[0]+" Position: "+ results[1]);
System.out.println("Run time: " + (endTime-startTime));
s.boardShow();
}
