What is a good algorithm to generate a random path?

Question

I need to generate a random path with 25 segments that never crosses itself between two locations in a 1000x1000 area. What is a good algorithm to do this?

My initial idea, which generates ok results, was to generate a random polygon using the space partitioning method and then remove one side.

The results look like this:

The downside of this method is that the start is always fairly close to the end (since they were originally connected by a line).

The other downside is since they were a polygon, the overall shape is generate some form or distorted circle. There are lots of types of paths that would never be generated, like a spiral.

Does anybody know an algorithm that could help me generate these paths?

Unrest

Answer 1

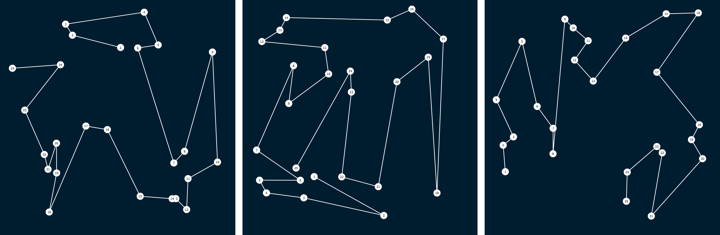
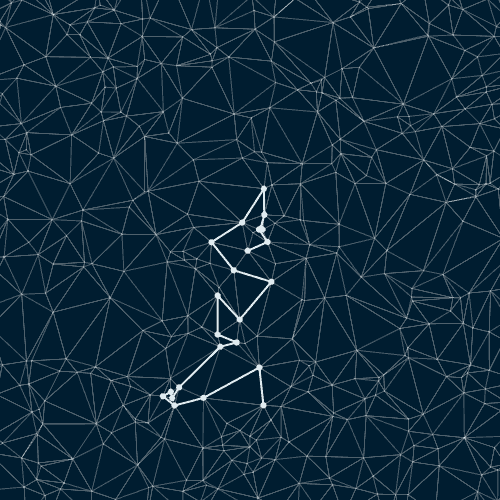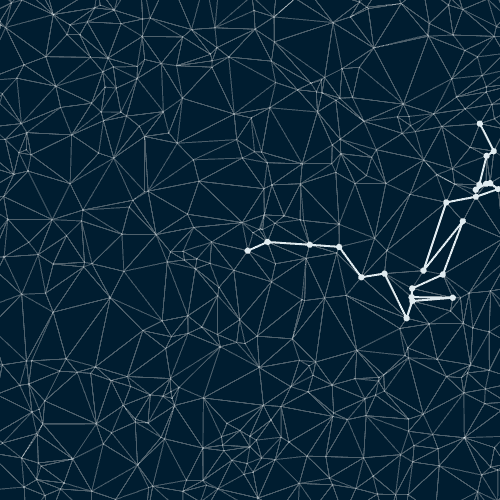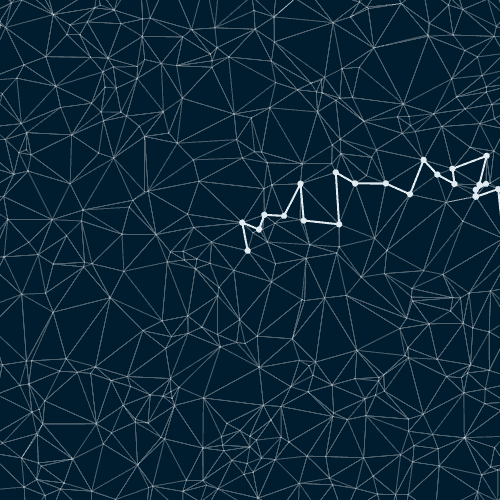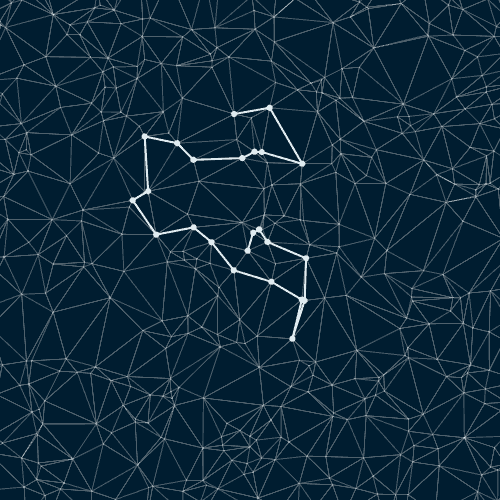
Triangulating a point set then walking over edges is a solution that avoids the problem with "circular-like" paths that polygon-based walks have.

You probably don't want a random point set that has points too close together because it may lead to a path looks like it's intersecting itself at certain points. For this reason, using something like a poisson disk sampling method to generate the point set is advisable — the triangulation of such a point set will provide a random path with segments of more-or-less equal length, segment-segment angles of roughly 60° and no apparent points of intersection.

Algorithm

With a Delaunay triangulation library at hand, the algorithm looks like this:

To initialise,

• Generate point set
• Triangulate point set
• Choose a random vertex from the triangulation (the lastVisitedVertex)

Then loop:

• Select a random edge connected to the last visited vertex, only if the other vertex connected to the edge has not yet been visited (this edge is the next segment)
• Mark the vertex we just came from as visited
• lastVisitedVertex = selected edge's other vertex
• Loop again, or exit if the path length exceeds our desired length (i.e. > 25)

Illustrations

Random paths on a triangulated poisson disc point set

[

Random paths on a triangulated random point set

Code

Here's an example in Java using the Tinfour library for triangulation. When using a library for triangulation, I advise you to pick one that provides easy access to connected edges for a given vertex, and the vertices making up a given edge.

In this example I pick a random edge (rather than vertex) as the starting point.

ArrayList<Vertex> randomPath(List<Vertex> randomPoints, int pathLength) {

    IncrementalTin tin = new IncrementalTin(10);

    tin.add(randomPoints, null); // insert point set; points are triangulated upon insertion

    HashSet<Vertex> visitedVertices = new HashSet<>();
    ArrayList<Vertex> pathVertices = new ArrayList<>();

    IQuadEdge lastEdge = tin.getStartingEdge(); // get random edge

    int n = 0;
    while (n <= pathLength) {

        List<IQuadEdge> list = new ArrayList<>();
        lastEdge.pinwheel().forEach(list::add); // get edges connected to A; add to array
        IQuadEdge nextEdge;
        int attempts = 0;
        do {
            nextEdge = list.get(random.nextInt(list.size())); // randomly select connected edge
            if (attempts++ > list.size() * 4) {
                return pathVertices; // path ended prematurely (no possible edges to take)
            }
        } while (visitedVertices.contains(nextEdge.getB()) || nextEdge.getB() == null);

        lastEdge = nextEdge.getDual(); // A and B flip around, so A is next vertex
        pathVertices.add(lastEdge.getB()); // add the point we just came from to path
        visitedVertices.add(lastEdge.getB()); // add the point we just came from to visited vertices
        n++;
    }
    return pathVertices;
}

Zoogeography

Answer 2

Here's an idea (disclaimer: off the top of my head, not tested, validated or anything...):

Draw random coordinates and "try" to connect lines in the order you draw - so you have P1_{(x1, y1)} then P2_{(x2, y2)} and you connect them, then P3_{(x3, y3)} and as long as no intersection is created (you have to test that every time), you keep drawing and connecting. Eventually, an intersection will be generated - you then try to connect the last point (Pn-1: prior to the newly created point) to the earlier of the two points forming the intersected line (let's call these Pi & Pi+j. If that's valid (meaning, it doesn't cross any other line) you disconnect that line (Pi+j no longer comes after Pi), you connect Pi with Pn-1 and resume from Pi+j (which now becomes Pn-1 in terms of point order). If connecting Pn-1 to Pi is invalid you do the same thing but with the newly found intersection.

Eventually you'll resolve the intersection(s) and will connect to the latest point - Pn and you can resume normally.

The obvious downside of this algorithm is that it has a very dangerous Big-O time complexity, but it should be able to generate all kinds of paths.

In terms of implementation data structure, a doubly linked list seems like an immediate candidate.

Cracker

What will be the approach If the path mechanism need to maintain 4 neighbor? – Gantt